核心問題統(tǒng)領下度量一致性的教學策略

陳蕓蕓 方麗紅

【摘?? 要】“角的度量”是“圖形與幾何”領域的重要教學內容之一，其教學目標是理解度量的本質。教師基于對“教學缺失了什么？”“學習忽視了什么？”的分析，以問題為統(tǒng)領，通過“提煉核心問題”“設計學習任務群”“構建遞進式問題鏈”等策略，推進“時間與角度”的教學，引導學生感悟度量的內在一致性，促進學生思維的分層進階，提升學生的量感素養(yǎng)及分析問題、解決問題的能力。

【關鍵詞】核心問題；問題鏈；度量；量感

“角的度量”是“圖形與幾何”領域的重要教學內容之一，其教學目標是理解度量的本質，即被度量對象中含有多少個度量單位。教學這一內容時，教師需要引導學生運用已有的知識經(jīng)驗，基于對“角”的定性描述，通過定量刻畫，深入理解“角”。另外，角度與鐘面具有天然的聯(lián)系。例如角的度量工具“量角器”是把圓平均分成360份，取其中的一半構成的。而鐘面上的一大格是將圓平均分成12份，一小格則是將圓平均分成60份。這兩者都指向度量單位的統(tǒng)一，體現(xiàn)了度量的一致性。因此，筆者嘗試以核心問題為統(tǒng)領，將“時間”與“角度”整合起來進行教學。通過層層遞進的問題鏈，驅動學生進行操作、探索和發(fā)現(xiàn)，感悟度量的內在一致性，促進學生的深度學習，從而實現(xiàn)學生思維的分層進階。

一、研讀教材：“角的度量”教學缺失了什么？

人教版教材在四年級上冊編排了“角的度量”單元，主要包括兩部分內容：一是線和角的認識，二是角的度量。在此之前，學生已在一維空間度量（長度）和二維空間度量（面積）的學習過程中積累了豐富的度量經(jīng)驗。但角的度量與長度、面積等的度量存在差異，它對學生而言是一個全新的知識領域。因此，有必要將其關聯(lián)起來，促進學生感悟度量的一致性。

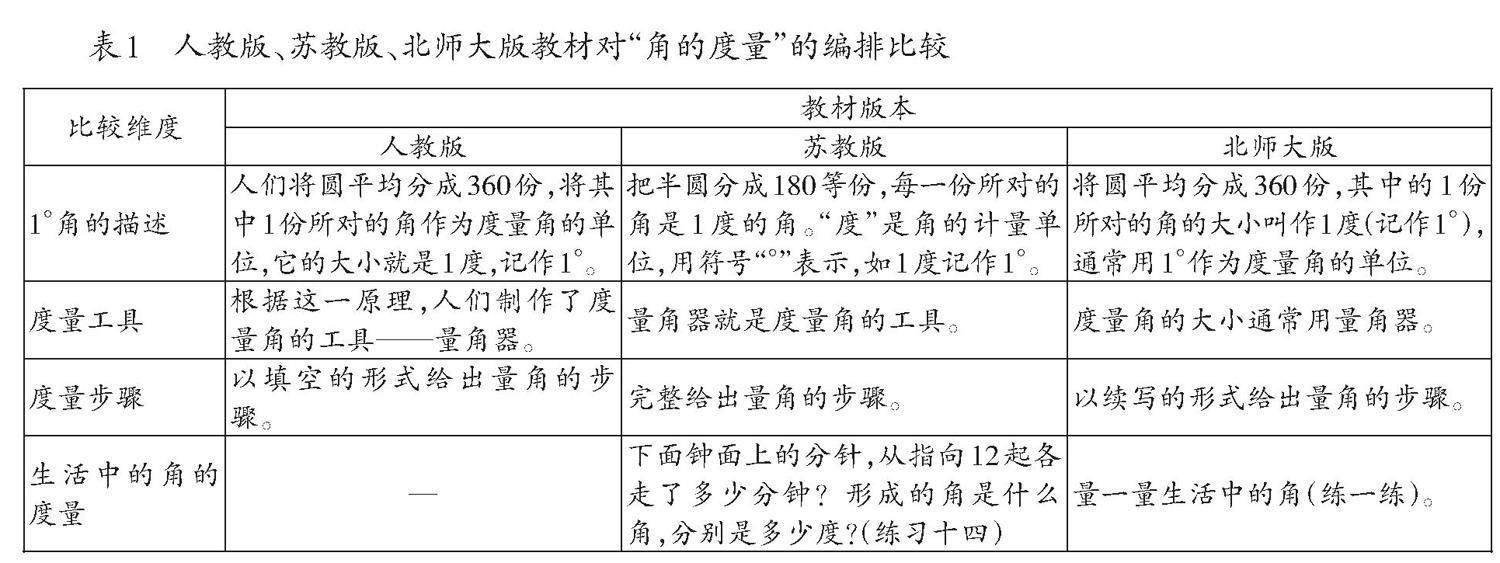
張奠宙教授將度量的本質歸納為“三性”，即正則性、有限可加性和運動不變性。其中，正則性是指度量標準與度量對象屬性的一致性，并將度量標準規(guī)定為“1”。為了更好地把握角的度量的教學，筆者對人教版教材、蘇教版教材和北師大版教材進行了橫向比較（如表1），發(fā)現(xiàn)各版本教材都將“角的度量”安排在四年級上冊，并且都包含以下內容：（1）提出統(tǒng)一度量單位的必要性，并對1°角進行描述；（2）引出度量工具——量角器；（3）給出量角的步驟。然而，這幾個版本的教材均未對度量工具、度量步驟等背后的原理進行解釋。換言之，教材內容在凸顯度量本質方面存在缺失。

進一步比較三個版本教材在習題設計方面存在的差異，發(fā)現(xiàn)：人教版教材并未直接嵌入生活中角的度量的相關內容，而蘇教版教材和北師大版教材則均將角的知識與生活實際相結合，引導學生運用角的度量這一學科知識解決生活中的問題。由此可見，人教版教材在生活中角的度量內容的編排上存在不足。

為此，筆者整合一至三年級的時間問題與四年級上冊的角的度量的教學內容，設計了一節(jié)拓展課。通過探究“鐘面上指針所表示的時間與角度關系”的活動，引導學生深入理解度量的本質，提升分析問題和解決問題的能力，全面發(fā)展量感這一核心素養(yǎng)。

二、研判學情：“角的度量”學習忽視了什么？

為了全面、準確地了解學生對“鐘面上指針所表示的時間與角度關系”的認知水平，在完成“角的度量”單元內容的教學后，筆者針對本校四年級學生（使用人教版教材）展開了一次前測調查與分析。

（一）調查對象及方法

以本校四年級175名學生為調查對象，采用書面前測探究單的形式展開調查，要求學生在15分鐘內獨立完成。

（二）調查內容與分析

【前測題1】學習了“角的度量”相關知識后，你認為鐘面上指針所表示的時間與角度之間存在聯(lián)系嗎？請舉例說明。

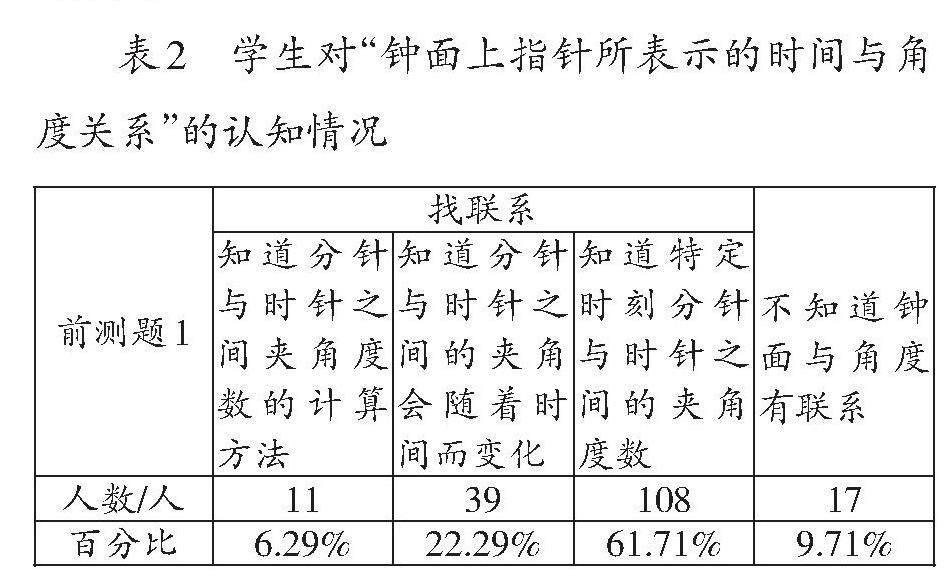
本題旨在了解學生對“鐘面上指針所表示的時間與角度關系”的認知情況，并考查學生這一認知的來源，初步掌握學生的認知基礎。調查結果如表2所示。

表2 學生對“鐘面上指針所表示的時間與角度關系”的認知情況

[前測題1?????? 找聯(lián)系

不知道鐘面與角度有聯(lián)系??? 知道分針與時針之間夾角度數(shù)的計算方法?????? 知道分針與時針之間的夾角會隨著時間而變化?????? 知道特定時刻分針與時針之間的夾角度數(shù)?????? 人數(shù)/人?? 11??? 39??? 108? 17??? 百分比??? 6.29%???? 22.29%?? 61.71%?? 9.71%?????? ]

從表2來看，近90%的學生能在一定程度上認識到鐘面上指針所表示的時間與角度之間存在聯(lián)系。進一步分析學生的答題情況，發(fā)現(xiàn)有61.71%的學生僅能依賴“直角＝90°、平角＝180°”的認知，描述特定時刻鐘面上的夾角度數(shù)。

【前測題2】請你用自己的話說一說，3時整鐘面上分針與時針的夾角是多少度？你是怎么得到的？

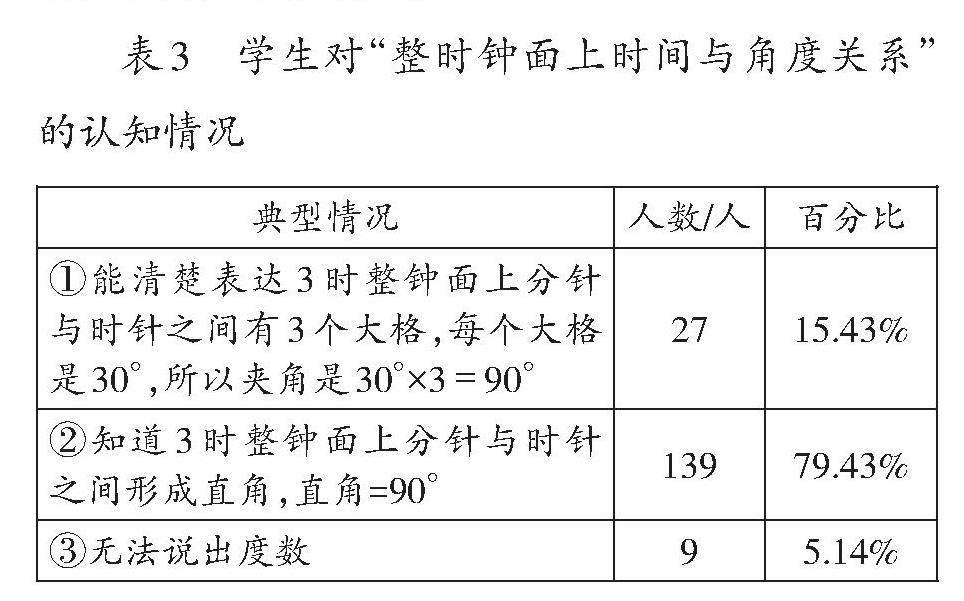
本題通過引導學生用語言描述3時整鐘面上分針與時針之間夾角的度數(shù)，調查他們對整時鐘面上分針與時針夾角度數(shù)度量情況的掌握程度，進而了解他們對時間與角度度量一致性的理解程度。調查結果如表3所示。

從表3中可以看出，大部分學生是基于“直角＝90°”的認知得出3時整鐘面上分針與時針之間夾角的度數(shù)的。

綜上所述，“角的度量”的學習活動忽視了兩方面內容：一是角的度量與生活的聯(lián)系，二是對角的度量本質的理解。因此，借助生活中熟悉的鐘面，將時間度量與角度度量的本質建立聯(lián)系，有助于進一步發(fā)展學生的量感，提升其分析問題與解決問題的能力。

三、教學實踐：“角的度量”價值追尋的本質是什么？

“角的度量”價值追尋的本質是什么？為解決這一問題，筆者基于上述對教材和學情的分析，確立了拓展課的教學目標：通過“鐘面上指針所表示的時間與角度關系”的探究活動，感悟度量的內在一致性，理解度量的本質，進一步提升量感素養(yǎng)，發(fā)展推理意識及分析問題、解決問題的能力。在教學過程中，筆者嘗試以核心問題為統(tǒng)領，以問題鏈為主線，設置由淺入深的遞進式問題鏈，驅動學生進行深度學習，將學生的思維逐步向縱深推進。

（一）提煉核心問題，明晰學習任務板塊

核心問題是指針對教學目標和重難點所提出的關鍵問題。它不僅指向知識的本質，還具備提綱挈領的作用。在提煉核心問題時，首先要深入研讀教材，明確教學目標及重難點，并結合學生實際情況，精心設計一組既相對獨立又互相關聯(lián)的核心問題，形成具有邏輯性和整體性的問題鏈，從而明晰學習任務板塊。

例如，基于對教材和學情的分析，首先明確“時間與角度”拓展課的核心內容為鐘面上指針所表示的時間與角度的關系，指向度量的本質。接著提煉出三個核心問題：（1）整時時刻，鐘面上指針所表示的時間與角度具有怎樣的關系？（2）半時時刻，鐘面上指針所表示的時間與角度具有怎樣的關系？（3）幾時幾分，鐘面上指針所表示的時間與角度具有怎樣的關系？（如圖1）

這三個核心問題既具備獨立的思考空間，又呈現(xiàn)出層層遞進的態(tài)勢。學生從對整時時刻時間與角度關系的初步感知，逐步深入對半時時刻時間與角度關系的理解，進而達到對幾時幾分時間與角度關系的有機拓展，知識內容得到有效外延。

（二）設計學習任務群，推進結構化學習

在設計學習任務群時，教師應以核心問題為中心，以提升學生自主探究能力為目標，同時關注學生在完成學習任務過程中的自主積極性，通過學習任務群驅動學生進行深度思考和全面探究，喚醒學生原有知識經(jīng)驗中與核心問題相關的知識、技能與方法，逐步實現(xiàn)“感知—領悟—內化”的結構化學習。

例如，對“時間與角度”中的三個核心問題進行分解，設計出“畫一畫、算一算、說一說”等學習任務群（如表4），既能引導學生逐步深入探究，又能激發(fā)學生的自主思考，強化對“鐘面上指針所表示的時間與角度關系”的理解。

在此教學過程中，學生享有充分的思考時間、自主探究的空間以及充分表達的機會，能夠全身心地投入到層次化的認知活動中，體驗數(shù)學問題完整的探究過程，并建立核心問題之間的本質聯(lián)系。

（三）構建遞進式問題鏈，促進思維分層進階

問題鏈是教學思路的具體化體現(xiàn)，具有較強的可操作性。在核心問題統(tǒng)領下，教師要設計具有邏輯關系的遞進式問題鏈，為學生搭建一個個“問題臺階”，提供可視化支架，引發(fā)學生的主動思考與自主建構，使其理解層層深入，促進數(shù)學思維的分層進階。

例如，針對核心問題2“半時時刻，鐘面上指針所表示的時間與角度具有怎樣的關系？”，教師可以設計以下子問題。

子問題①：觀察這三個鐘面，你有什么想說的？

教師先出示一個典型的錯誤作品（如圖2），提問：“觀察這三個鐘面，你有什么想說的？”學生發(fā)現(xiàn)：三個鐘面上的時針都畫錯了，三個半時的時針都沒畫到一大格的中間。

子問題②：從12時到12時半，分針走過半圈，時針走過多少度？

子問題③：12時半，分針與時針之間的夾角角度是怎么確定的？

子問題④：對比這三個半時時刻分針與時針之間的夾角度數(shù)，你有什么發(fā)現(xiàn)？

子問題⑤：半時時刻，分針與時針之間的夾角度數(shù)是怎么推導出來的？

在上述教學過程中，通過一系列子問題的逐一解決，學生逐步推導出半時時刻鐘面上指針所表示的時間與角度的關系，并與整時時刻建立聯(lián)系，初步構建“鐘面上指針所表示的時間與角度關系”的數(shù)學模型。如此，教師以“淺入深出”的方式，引導學生深入學習，促使學生理解鐘面上的度量一致性，進一步感悟度量的本質。

總之，問題鏈的設計驅動學生進行深度思考和充分探究，使深度學習成為現(xiàn)實。教師積極構建并實施遞進式問題鏈教學，有助于學生深入理解知識的內涵和外延，為學生的知識獲得和能力發(fā)展提供了充分的空間，從而發(fā)展其思維能力，培養(yǎng)其核心素養(yǎng)。

參考文獻：

［1］鮑善軍，朱曙光.“一題一課”的教學價值、設計與策略［J］.教學月刊·小學版（數(shù)學），2022（7/8）：12-16.

［2］鄭毓信.中國數(shù)學教育的“問題特色”［J］.數(shù)學教育學報，2018，27（1）：1-7.

［3］陳黎春.聚焦度量本質?? 促進量感發(fā)展：“角的度量”教學片斷與思考［J］.小學數(shù)學教育，2023（22）：44-47.

（浙江省杭州市錢塘區(qū)河莊小學）