借助遷移式問題鏈 構建運算的一致性

馮佳美

【摘?? 要】《義務教育數學課程標準（2022年版）》在“數與運算”主題中明確指出，要讓學生“體會數的運算本質上的一致性”。在教學“小數四則運算的再認識”這一內容時，教師以核心內容“計數單位統領小數四則運算的一致性”為統領，以問題鏈為抓手，設計了“關聯加減、遷移乘法、類比除法”的遷移式問題鏈，以建立小數加、減、乘、除法之間的聯系，幫助學生理解“數的運算”的核心本質，感悟運算的整體性與一致性，從而培養學生的運算能力、推理意識和模型意識。

【關鍵詞】遷移式問題鏈；運算的一致性；小數四則運算

《義務教育數學課程標準（2022年版）》在“數與運算”主題中指出，要讓學生“感悟數的運算以及運算之間的關系，體會數的運算本質上的一致性，形成運算能力和推理意識”。然而，五年級學生在學完小數四則運算后，對四則運算的理解往往是孤立的，缺乏對小數運算算理一致性的全面認識。

從教材的編排情況來看，在小數加減法的學習中，學生受整數加減法正遷移的影響，能夠較好地理解并掌握小數加減法的運算意義。然而，在小數乘除法的學習中，教材并未結合小數乘除法的運算意義展開教學，而是引導學生依據積的變化規律和商的變化規律，將其轉化為整數乘除法進行運算。這在一定程度上強化了學生對算法的掌握，弱化了學生對算理的理解。因此，引導學生建立小數加、減、乘、除法之間的聯系，融通算理與算法，整體構建運算的一致性，成為教學中的重要內容。

問題是教學的核心，也是推動學生思維發展的關鍵因素。在教學中，教師可以通過設計問題鏈，有效支持學生經歷數學知識的形成與建構過程。在教材中小數四則運算相關內容教學結束后，筆者設計了“小數四則運算的再認識”這一教學內容，在核心內容“計數單位統領小數四則運算的一致性”的統領下，以問題鏈為抓手，設計了“關聯加減、遷移乘法、類比除法”的遷移式問題鏈。通過問題鏈幫助學生建立小數加、減、乘、除法之間的聯系，深化學生對運算整體性與一致性的理解，從而培養學生的運算能力、推理意識和模型意識。

一、聚焦核心內容：計數單位統領小數四則運算的一致性

核心內容體現了數學學科本質，有助于揭示知識間的內在聯系，具有很強的遷移價值。因此，深入理解與把握核心內容，能夠幫助學生將零散的知識點串聯起來，形成知識網絡，從而實現知識與方法的遷移應用。那么，運算一致性的核心內容是什么？對此，史寧中教授指出：數的建構與數的運算都是基于計數單位進行的，所有的運算都是相同計數單位個數的變化。加法是計數單位個數的合并，減法是計數單位個數的拆分，乘法是計數單位個數的累加，除法則是計數單位個數的遞減。因此，運算一致性的核心內容就是計數單位。

（一）計數單位如何統領小數加減法？

在進行小數加減法運算時，首先要統一計數單位，然后再計算計數單位的個數。例如，在計算小數加法0.42+0.3時，可以將其看作“4個0.1加3個0.1加2個0.01”，結果為“7個0.1加上2個0.01”。但這種表示方式不能直觀顯示計數單位的個數，故教師可以將計數單位統一為更小的單位，如0.01，把加法運算變為“42個0.01加30個0.01”，結果得到“72個0.01”。減法運算同理。如0.42-0.3可以看成“42個0.01減30個0.01”，結果為“12個0.01”。因此，在計數單位的統領下，小數加減法的運算體現為計數單位不變，計數單位的個數相加減。

（二）計數單位也可以統領小數乘除法嗎？

在小數乘除法運算中，計數單位相較于小數加減法有所變化。具體表現為：在進行小數乘法計算時，如計算0.2×0.3，可先將其轉化為“（2×0.1）×（3×0.1）”，再簡化為“（2×3）×（0.1×0.1）”，最終得到“6×0.01”。在這一過程中，新計數單位通過兩個原計數單位相乘得到。在進行小數除法計算時，如計算0.06÷0.3，可先將其轉化為“（6×0.01）÷（3×0.1）”，再簡化為“（6÷3）×（0.01÷0.1）”，最終得到“2×0.1”。這里的計數單位則是通過兩個原計數單位相除得到。盡管小數乘除法的計數單位有所變化，但其核心依然是圍繞計數單位的個數進行計算。無論是乘法還是除法，都可以歸納為“計數單位與計數單位進行運算，計數單位上的數字與計數單位上的數字進行運算”。

綜上所述，以計數單位為核心內容教學小數乘除法，不僅可以使教學內容保持前后連貫，還能幫助學生整體建構對小數乘除法的理解。

二、提煉核心問題：小數四則運算一致性的遷移式問題鏈

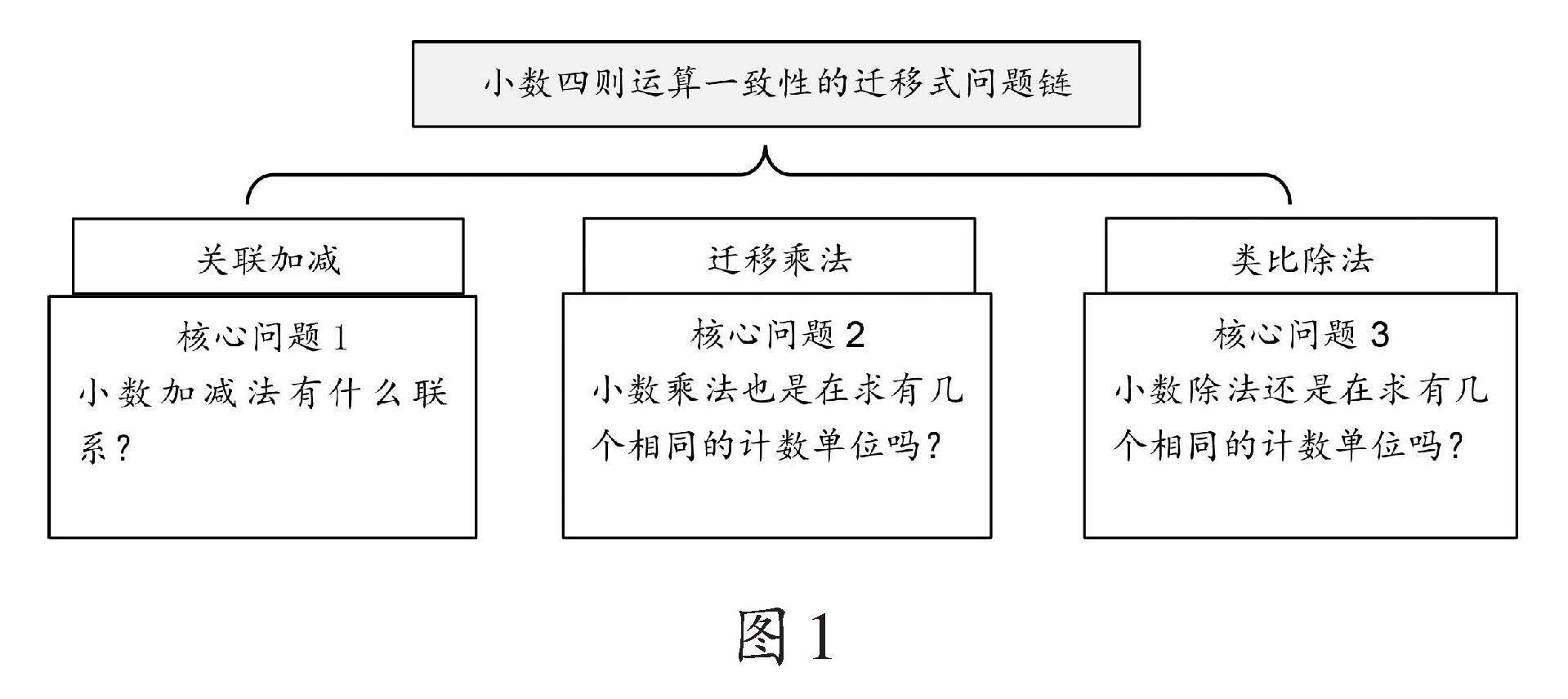
鄭毓信教授曾強調，“問題引領”的研究重點是“核心問題的提煉與加工”。教師應基于教材編排內容，立足實際學情，聚焦核心內容，精準提煉核心問題。在此基礎上，對提煉的問題進行深度加工，形成問題鏈，以鏈條式結構為學生提供清晰的學習主線。在“小數四則運算的再認識”這一內容的學習中，教師以小數加法為學習起點，進一步設計“關聯加減、遷移乘法、類比除法”的遷移式問題鏈，為學生的探究與遷移搭建支架（如圖1）。

（一）關聯加減，尋找一致性的“敲門磚”

在這一內容的學習之前，學生已掌握了小數加減法的運算意義。為此，教師從加法運算開始教學，先讓學生借助“百格圖”涂色表示“0.42+0.3”，再引導學生思考應如何表示“0.42+0.3”的涂色過程。是選擇4個0.1加上3個0.1，再加上2個0.01，還是選擇42個0.01加上30個0.01？大多數學生是選擇42個0.01和30個0.01進行涂色的，因為在統一計數單位0.01后，可以直接看出計數單位的個數。由此得出，小數加法的算理是“求有幾個相同的計數單位”。在此基礎上，教師引導學生將這一學習經驗順向遷移至小數減法的算理表達上，以促進他們對小數加減法算理共性的深入思考。

有了加法運算的基礎，學生在學習減法運算時表現出較高的水平。教師教學時，先分析學生的涂色作品，再讓他們結合相應的算式進行表達。例如，0.42-0.3可以表示為“42個0.01減30個0.01，還剩下12個0.01”。接著引導學生思考發現：小數加減法之間的算理共性在于一致性，這也是整體建構的關鍵點。因此，核心問題“小數加減法之間有什么聯系”成為將知識遷移到小數乘法的“敲門磚”。

（二）遷移乘法，打通一致性的“隔斷墻”

小數乘法雖然和小數加減法一樣，都表示“求有幾個相同的計數單位”，但與小數加減法不同的是，原來的兩個計數單位相乘會創生新的計數單位。因此，感悟乘法“計數單位的變化”就成為建構運算一致性的“隔斷墻”。

在初步感悟“求有幾個相同的計數單位”之后，學生自然會產生猜想：“小數乘法會不會也是在求有幾個相同的計數單位？”于是教師引導學生計算0.2×0.3，并比較（2×3）×（0.1×0.1）與（2×3）×0.1兩種結果，分析其計數單位是0.1還是0.01（即0.1×0.1）。根據計算結果0.06，學生能夠準確判斷出計數單位為0.01。但隨之也會產生疑問：“為什么計數單位是0.01？”為此，教師引導學生通過“畫一畫”“找一找”“說一說”等活動，感悟小數乘法計數單位變化的原理。學生在充分探究后，通過與小數加減法算理進行比較，發現小數乘法的算理也是“求有幾個相同的計數單位”，不同的是計數單位發生了變化，原來的兩個計數單位相乘產生了一個新的計數單位。

（三）類比除法，鞏固一致性的“頂梁柱”

“小數除法還是在求有幾個相同的計數單位嗎？”是本內容教學中的最后一個核心問題，也是建構運算一致性的“頂梁柱”。為此，教師基于先前對小數加減法、小數乘法的融會貫通，充分利用直觀的微課，以幫助學生理解小數除法計數單位變化的原理。

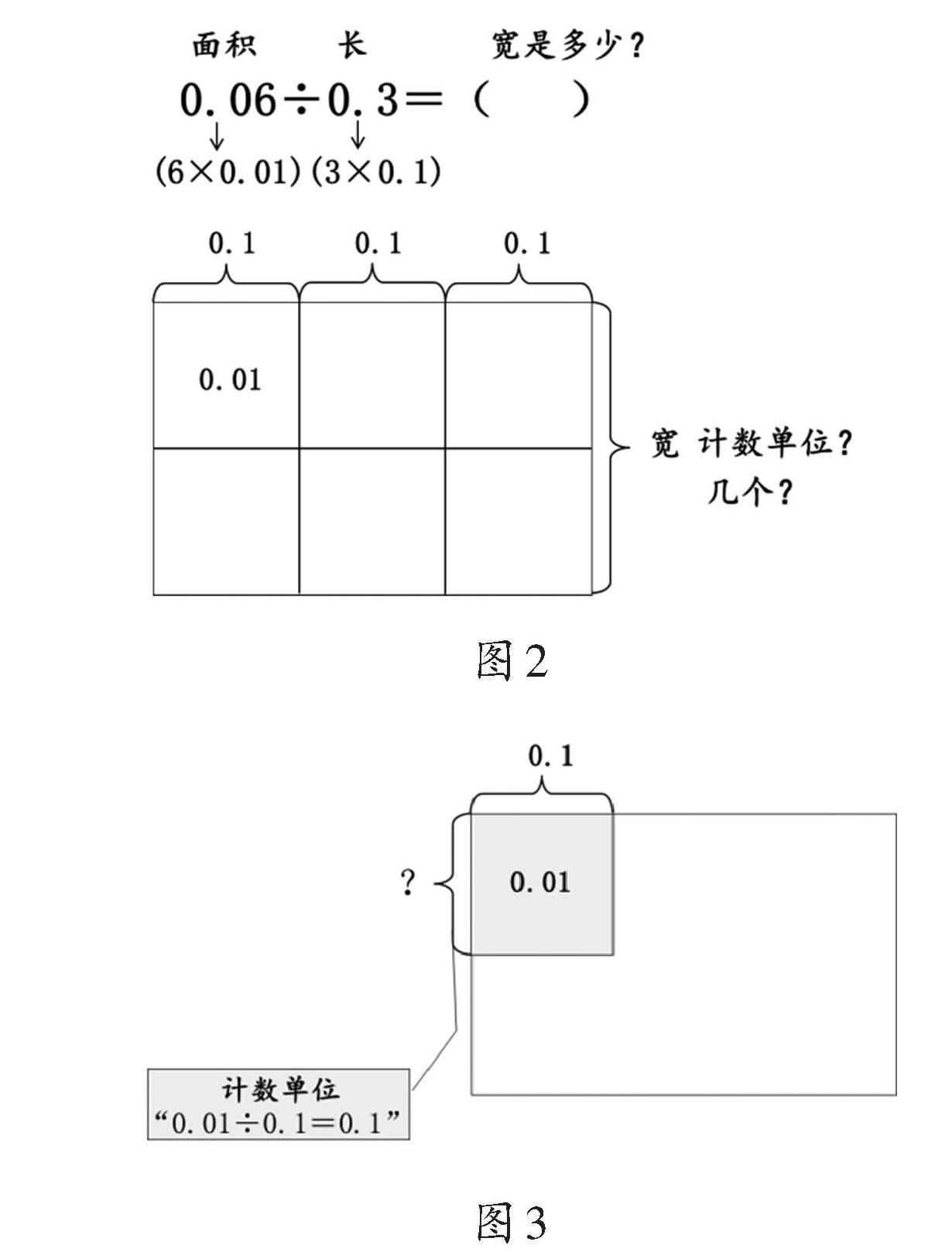
在教學0.06÷0.3的計算時，教師可以借助長方形的面積模型進行討論。通過將0.06視為長方形的面積，0.3視為長方形的長，從而將0.06÷0.3轉化為“已知面積和長，求寬是多少”的問題（如圖2）。那么，算式0.06÷0.3就是在求“寬有幾個這樣的計數單位？”，即求寬這部分的計數單位是多少，以及有多少個這樣的計數單位。確定寬這部分的計數單位個數，需要進行以下兩個關鍵步驟：第一步，確定計數單位。由圖3的涂色部分可知，正方形面積表示的計數單位是0.01。而長這部分的計數單位為0.1，故通過0.01÷0.1就可以求出寬這部分的計數單位，得到0.1。第二步，確定個數。長方形面積表示的計數單位有6個，其中一行有3個，可以排列成2行，由此可以得出0.1的個數為2個。最后，將求得的計數單位與個數相乘，就可得出寬為2個0.1。在上述師生討論的基礎上，教師再利用動態的微課進行講解，幫助學生進一步理解小數除法計數單位變化的原理。

遷移式問題鏈的教學是培養學生核心素養的重要抓手。教師應圍繞核心內容，設計核心問題，并以序列問題鏈為教學路徑，幫助學生建立知識與知識間的內在聯系，從而推進學生對知識本質的深刻理解，促進學生思維的發展。

參考文獻：

［1］中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］.北京：北京師范大學出版社，2022．

［2］鞏子坤，史寧中，張丹.義務教育數學課程標準修訂的新視角：數的概念與運算的一致性［J］.課程·教材·教法，2022，42（6）：45-51，56.

［3］鮑善軍，朱曙光.“一題一課”的教學價值、設計與策略［J］.教學月刊·小學版（數學），2022（7/8）：12-16.

［4］鄭毓信.中國數學教育的“問題特色”［J］.數學教育學報，2018，27（1）：1-7.

（浙江省杭州市錢塘區云帆小學）