氣候變暖影響下黃河源區潛在蒸發量預測不確定性研究
殷暉 白福青 馬金輝 田浩翔

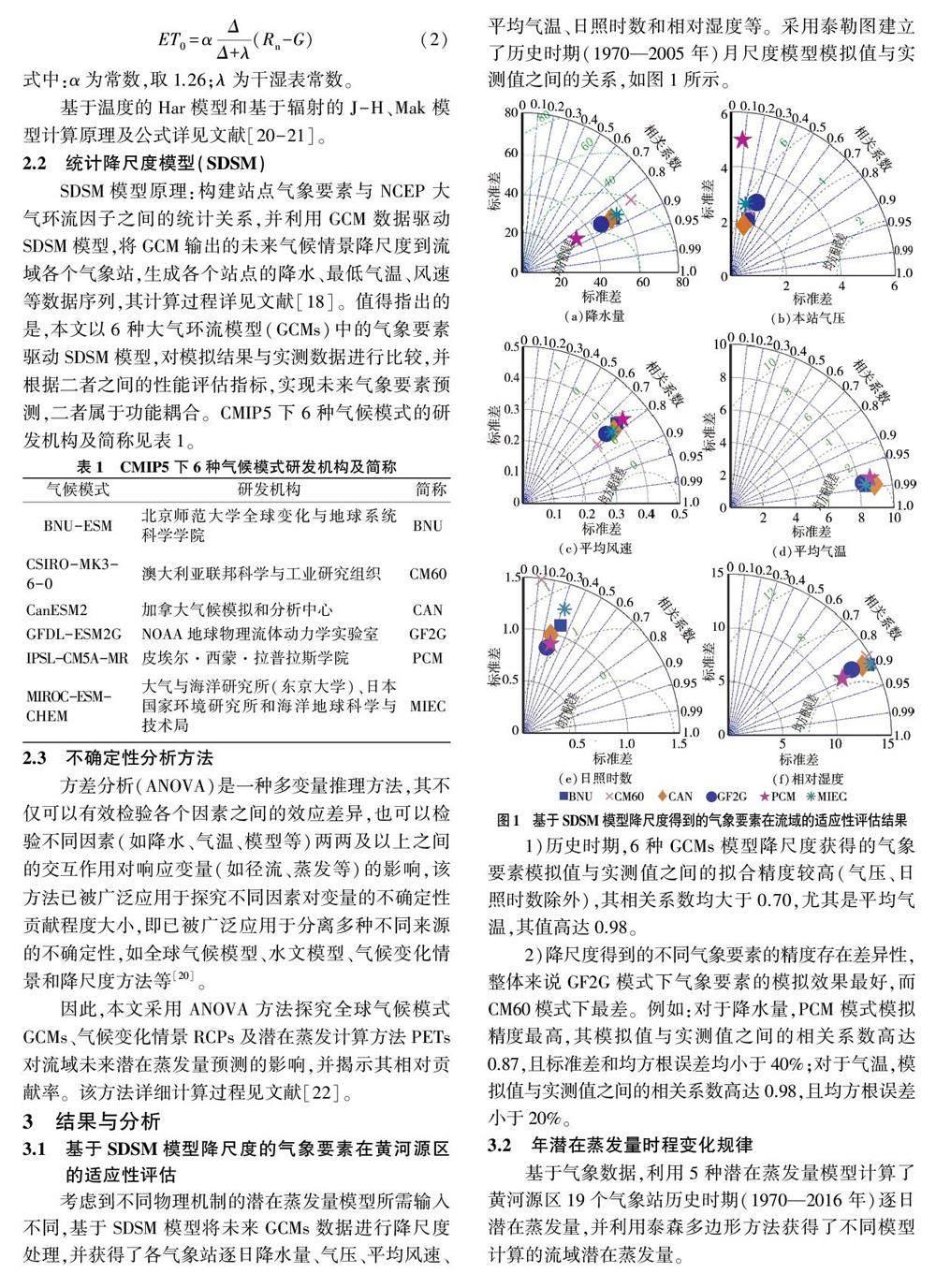
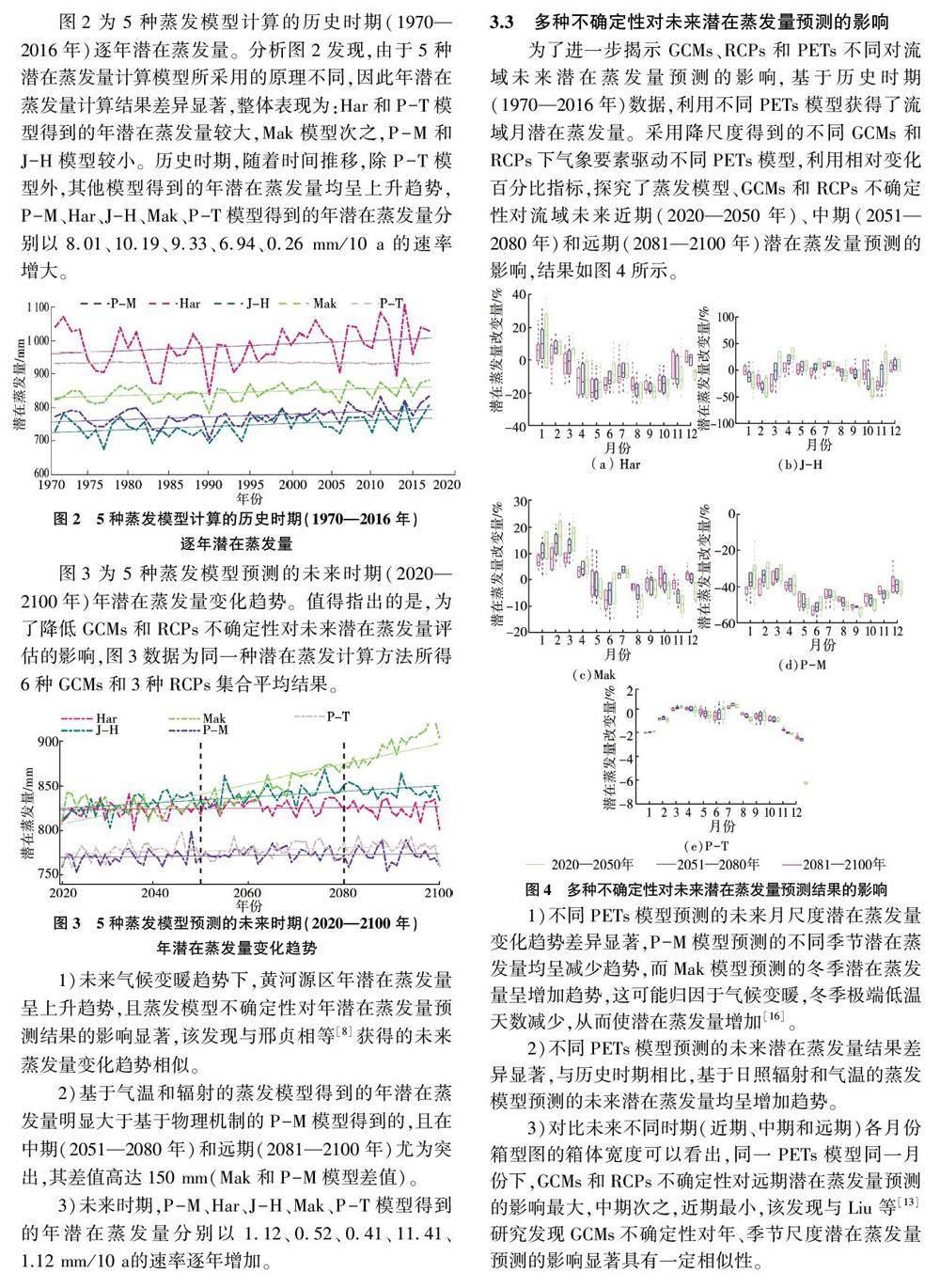
摘 要:蒸發是連接地表能量平衡和水量平衡的重要紐帶,高寒區蒸發量對氣候變暖尤為敏感。然而,高寒區蒸發預測存在大量不確定因素,其造成流域水文循環變化規律分析、水資源管理面臨嚴峻挑戰。因此,以屬于高寒區的黃河源區為例,利用5 種物理機制不同的蒸發計算模型(P-M、Har、J-H、Mak 和P-T)理清模型不確定性對流域潛在蒸發量預測結果的影響;通過耦合蒸發計算模型、GCMs 模型、RCPs 模型,探究多源不確定性對未來不同時期( 近期、中期和遠期) 潛在蒸發量預測結果不確定性的影響,并利用方差分析方法量化評估各因素獨立及交互作用對潛在蒸發量預測結果不確定性的貢獻。結果表明:基于太陽輻射和氣溫的潛在蒸發量模型獲得的潛在蒸發量明顯大于基于物理機制P-M 模型獲得的潛在蒸發量,其差值約為150 mm;RCPs 不確定性是導致蒸發預測結果不確定性的主導因素,占比高達65%,且多種不確定性因素的交互作用對蒸發預測結果不確定性的貢獻在春、冬季節尤為突出。
關鍵詞:氣候變暖;潛在蒸發量;預測不確定性;黃河源區
中圖分類號:TV213.8;TV882.1 文獻標志碼:A doi:10.3969/ j.issn.1000-1379.2024.05.008
引用格式:殷暉,白福青,馬金輝,等.氣候變暖影響下黃河源區潛在蒸發量預測不確定性研究[J].人民黃河,2024,46(5):50-55.
0 引言
高海拔寒冷地區(簡稱“高寒區”)蒸發量對氣候變暖尤為敏感,高寒區升溫速度是全球平均速度的兩倍[1] 。蒸發作為水循環過程中的重要分支,亦是連接地表能量平衡和水量平衡的重要紐帶。但受氣候變暖影響,流域水循環加劇,且水資源供需矛盾愈加突出[2-3] ,因此開展氣候變暖影響下高寒區潛在蒸發量預測不確定性研究具有重要意義,可為水資源優化管理、灌溉制度制定提供理論參考。
近年來,國內外學者針對流域蒸發量的時空演變規律及其預測不確定性開展了大量研究,并獲得豐碩的成果[4-5] 。在蒸發量時空演變規律方面,Nie 等[6] 以黑龍江流域為例,利用Mann-Kendall 趨勢檢驗法揭示了年尺度、季節尺度潛在蒸散發量的時空演變特征;左大幸等[7] 采用修正的Penman-Monteith(P-M)模型計算了1980—2019 年珠江流域的潛在蒸散發量,并利用Mann-Kendall 非參數檢驗、反距離權重等方法分析了潛在蒸散發量的時程變化趨勢;邢貞相等[8] 利用P-M模型計算了三江平原區的潛在蒸發量,并利用CMIP5下CanESM2 模式數據,預估了流域未來的潛在蒸發量,結果表明流域歷史和未來時期潛在蒸發量均呈上升趨勢;劉鳳鑫[9] 對比評估了4 種潛在蒸發量模型(雙源蒸發模型、彭曼公式、Dalton 公式以及波文比-能量平衡法)在本溪地區的適應性;Valle 等[10] 以巴西為例,綜合考慮太陽輻射、溫度要素,構建了21 種潛在蒸發量模型,揭示了其時空變化特征,并指出基于日照輻射的Priestly-Taylor(P-T)模型的計算精度較高。
在蒸發量預測不確定性方面,秦爽[11] 對比分析了CMIP6 下10 種氣候模式(GCMs)在漢江上游流域的適應性,結果發現不同GCSs 和預估情景(SSPs)對蒸發量的時空分布影響較大。高雅琦[12] 以太湖流域為例,基于CMIP5 中的HadCEM2 數據,利用湖泊模型模擬了未來流域的潛在蒸發量,發現不同氣候情景(RCPs)下太湖蒸發量增加,但蒸發量增加比例不同,且蒸發量的增加隨著輻射強迫的增大而增大。Liu等[13] 利用12 種GCMs 下氣象數據驅動PenPan 模型探究了不同GCMs 對年、季節和月尺度潛在蒸發量的影響,并指出不同GCMs 獲得的年和季節潛在蒸發量存在不同的變化趨勢。鄧曉宇等[14] 以東江流域為例,基于5 個氣候模式和3 種RCP 氣候情景預測了未來潛在蒸發量時空變化,發現RCP2.6 和RCP4.5 下流域蒸發量呈增加趨勢,但RCP8.5 下則呈減少趨勢。綜上,眾多學者利用不同蒸發量算法預估了未來潛在蒸發量的時空變化趨勢,并指出GCMs 和RCPs 均對蒸發量的評估產生重要影響,且表現方式不同,即不同GCMs、RCPs 和蒸發算法均改變了流域蒸發量的時空分布規律。然而,GCMs、RCPs 和蒸發算法不確定性對蒸發量預測結果不確定性貢獻究竟如何卻鮮有涉及。
因此,本文以屬于高寒氣候區的黃河源區為例,基于1970—2016 年逐日降水、氣溫、風速等氣象數據,利用5 種不同物理機制的潛在蒸發量模型,探究了歷史時期潛在蒸發量的時程變化規律;通過耦合統計降尺度模型(SDSM)和6 種大氣環流模型(GCMs),預測了未來潛在蒸發量的時程變化,并利用相對變化百分比指標,探究了蒸發模型、GCMs 和RCPs 不確定性對流域未來近期(2020—2050 年)、中期(2051—2080 年)和遠期(2081—2100 年)潛在蒸發量預測不確定性的影響,采用方差分析方法(ANOVA)量化分離了其對未來不同時期潛在蒸發量預測不確定性的相對貢獻。

