小學數學概念教學中數形結合思想的應用策略探究

馬秀玲

【摘要】小學數學概念教學內容較為抽象，教師直接教學易使學生產生畏難情緒.教師應用數形結合開展概念教學，可解決學生學習效能低等問題，提高其學習效率.文章展開說明數形結合在小學數學概念教學中的應用意義，結合“倍數與因數”課程教學案例研究其具體應用方法，指出教師可應用數形結合思想指導學生覺察概念表象，理解概念內涵，進行概念表達，等等，同時基于教學實踐提出幾點反思，期望為一線教師提供教學參考.

【關鍵詞】小學數學；概念教學；數形結合；策略

“數”與“形”是數學研究的主要對象，基于二者所衍生的數學概念十分豐富，包括整數、小數、分數及其四則運算的概念，三角形、平行四邊形、正方形、圓形及其周長、面積運算的概念，等等.數學概念通過揭示數學問題的本質屬性反映數學事物，具有抽象性、概括性特征.在小學階段，學生的思維處于初始發(fā)展階段，在學習復雜概念時，若教師直接采用灌輸手段強迫學生死記硬背相關概念，容易造成學生的機械識記問題，不利于其對概念的內化、吸收與遷移應用.數形結合思想提倡結合使用“數”與“形”兩類教學資源，指導學生直觀觀察、抽象分析，使其基于已有的知識、經驗探索新的數學事物，最終實現對數學概念的理解與應用.

一、數形結合思想在小學數學概念教學中的應用意義

根據多元智能理論，學生的智能包括語言智能、數理邏輯智能、空間智能等，且各項智能發(fā)展程度存在差異.此理論解釋了不同學生在學習相同數學概念時的表現差異，如部分學生很快理解了抽象的數學定義、公式，但還有一部分學生需要反復閱讀、思考、結合實例分析才能理解數學定義.數形結合思想將抽象的“數”與直觀的“形”有機結合，以具體圖形展示事物的數量關系，有利于學生理解其中蘊含的數學規(guī)律，對于各類學生理解數學概念有著積極的促進意義.

二、小學數學概念教學中數形結合思想的應用策略

概念反映事物的本質屬性，由確切的詞匯或符號作為載體.概念的形成是思維運作的產物，只有有效激活學生的直觀、邏輯、抽象等數學思維，才能夠使其基于已掌握的數學知識、思想方法及學習經驗抽象新的數學概念，并將其內化成自身的知識體系.教師在應用數形結合思想開展小學數學概念教學時，應明確學生的思維發(fā)展規(guī)律，先借助直觀可視的圖形引發(fā)學生的直觀認識，再巧妙運用數學圖示、數學公式驅動其對概念內涵的探究，使其在持續(xù)性學習過程中明確概念所表示的數學原理，掌握表示及應用數學概念的方式方法，建構完善的知識體系.下面，文章將結合“倍數與因數”課程教學案例，詳細論述應用數形結合思想落實概念教學的具體路徑.

（一）數形結合指導學生覺察概念表象

概念表象也可理解為意象，指的是當脫離觀察對象后，腦海中出現的事物形象.形成概念表象是抽象數學概念的前提.教師只有增強學生對數學研究對象的直觀認識，才能夠使其將數學事物的形象儲存在腦海當中，為后續(xù)的邏輯推理、數學抽象等學習奠定基礎.同時，小學生對現實事物具有較強的探索興趣，教師可基于此設計教學圖示，借助圖示內容呈現數學現象，使學生在觀察的過程中對圖示中的數量關系、空間形式形成感性認識，覺察概念表象.以“倍數與因數”一課教學為例，教師可借助生活中常見的事物設計直觀圖示并創(chuàng)設情境，引發(fā)學生對不同事物間“倍”的關系的覺察，為后續(xù)倍數、因數的概念剖析奠定基礎.

【情境】李華邀請3名同學來家做客，媽媽準備了一些蘋果和果盤，你能幫媽媽將果盤裝好分給同學們嗎？

在情境圖中，教師將蘋果排成3行6列，以便學生快速明確蘋果的總數，同時給出3個盤子，便于學生快速基于圖形內容確定擺放方案，使其在腦海中聯想已掌握的乘法、除法計算公式，如3×6=18，18÷3=6等，建立新問題與已掌握的數學理論知識的聯系.在此基礎上，教師可延伸情境內容，引發(fā)學生思考抽象問題：在此情境中，蘋果的數量是多少？它的數量是盤子數量的幾倍？如果將它平均分成3份，那么每份是多少個？蘋果所分成的份數、每份的個數與蘋果總數具有怎樣的數量關系？通過提問、追問加深學生對具體事物的印象，使學生在觀察、聯想的過程中將“蘋果”圖示抽象成3行6列的點子圖、小棒圖等，覺察“18是3，6的倍數”“3，6是18的因數”這一概念表象.

（二）數形結合幫助學生明確概念本質

數學概念反映了數學研究對象所具備而其他對象所不具備的屬性.教師要使學生明確數學概念的本質屬性，就需要引導學生深入探索，使學生先明確概念的基本含義，再探索概念的外延，確定該概念與其他概念的本質區(qū)別，實現深度理解.教師采取語言講解的方式指導學生探究概念，容易增加教學難度，影響學生的學習效率.因此，教師可應用數形結合思想，借助圖示直觀展示數學研究對象的特征，幫助學生在短時間內發(fā)現數學規(guī)律，明晰概念的本質.以“倍數與因數”一課教學為例，教師可借助圖示分別指導學生理解概念的內涵與外延，促進其知識體系的完整建構.

1.借助圖示指導學生理解概念的內涵

教師應用圖示輔助學生學習概念，需在圖形內直觀體現數學研究對象的內在數量關系與本質規(guī)律，幫助學生理解相關內容.例如，在“倍數與因數”一課概念教學中，教師提出問題，并要求學生借助方格圖解決問題，使學生在識圖、畫圖、觀察與分析的過程中感悟圖形內蘊含的倍數與因數的數量關系，實現深度理解.

【問題】用12個同樣大的正方形拼成一個長方形，可以擺幾排，每排擺幾個？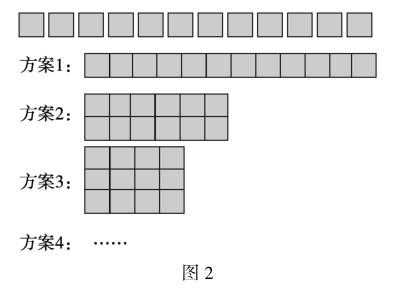

基于圖示，教師可分以下幾步展開概念理解教學：

步驟1：圍繞具體圖示組織學生觀察12個正方形拼成了怎樣的長方形，要求學生數出長方形的長是多少，寬是多少.在此過程中，教師指導學生由“形”的觀察學習向“數”的分析學習過渡，使學生發(fā)現數學規(guī)律：12個正方形可拼成長為12、寬為1的長方形，長為6、寬為2的長方形，長為4、寬為3的長方形.

步驟2：圍繞“倍數與因數”的相關概念，要求學生思考表示長方形長、寬的數與正方形總數存在怎樣的數量關系，可用怎樣的數學公式來表達.在此過程中，教師驅動學生列出1×12=12，2×6=12，3×4=12，4×3=12，12÷1=12，12÷2=6，12÷3=4等算式，初步形成1的12倍是12，2的6倍是12等認識.

步驟3：基于學生發(fā)現的數學規(guī)律展示具體概念，例如，假如一個整數能夠被另一個整數整除，這兩個整數就存在倍數關系，比如12÷1=12中，12可以被1整除，說明12是1的倍數；假如一個整數乘一個整數得到另一個整數，那么這兩個整數可被稱為另一個整數的因數，以1×12=12為例，1乘12等于12，那么1與12是12的因數.

2.借助圖示指導學生明確概念的外延

概念的外延指的是具有概念所反映的特有屬性的具體對象的總和，說明了概念所反映的事物具體有哪些.概念的外延與其內涵具有相互聯系的關系.以“倍數與因數”一課教學為例，質數、合數、公因數、公倍數等都是倍數與因數兩個概念的外延.教師指導學生明確概念的外延，可使學生進一步確立數學課程學習的界限，深化其對概念所表示的數學本質屬性的理解.在實際教學中，教師可借助恰當圖示表示概念的外延，指導學生明確概念、子概念之間的關系.

比如，教師可借助小棒圖（見圖3）直接呈現具體案例，指導學生在識圖的過程中理解質數、合數的基本含義.

再如，教師可應用Venn圖（見圖4）展示概念與概念外延的關系，加強學生對不同概念間具體關系的理解.

這樣，教師結合Venn圖直觀展示倍數、因數兩個概念之間的不相容關系，質數、合數、公因數與因數的種屬關系，2，3，5的倍數、公倍數與倍數的種屬關系，使學生明確倍數與因數的概念界限，進一步強化學生對概念教學內容的認知.

（三）數形結合促進學生學會概念表達

教師基于點子圖、表格圖、小棒圖等圖示指導學生認識數學事物，之后由自己引出概念，講解相關內容，固然可促進學生對相關內容的認知.但是，教師若重復使用上述教學方式，容易使學生產生惰性思維，導致學生養(yǎng)成被動接受學習的習慣.為了避免此類問題出現，教師還應在教學中變換教學策略，指導學生依靠圖示內容獨立抽象數學概念，使學生在自主發(fā)現、自主探究的過程中建構數學模型，培養(yǎng)學生形成自主學習的思維習慣.為此，教師可結合概念教學主題為學生提供相應的學習支架，如恰當的數學圖形、具有啟發(fā)性的問題等，借助此類內容驅動學生運用數形結合的思想方法發(fā)現數學規(guī)律，運用建模的思想方法進行數學表達，從根本上提高思維水平.以“倍數與因數”一課教學為例，教師可出示圖片（見圖5），組織師生對話，引導學生看圖推理，總結概念.

師：觀察點子圖，淺色點子的分布有什么規(guī)律？

生：從第一行開始從左向右數，第3個、第6個、第9個、第12個點子都是淺色的.

師：你發(fā)現了什么規(guī)律？

生：淺色的點子排列數均為3的倍數.

師：第11個點子是淺色的嗎？第12個和第13個呢？你發(fā)現3的倍數具有怎樣的規(guī)律？

生：11÷3=3……2，第11個點子是深色的，12÷3=4，第12個點子是淺色的.我發(fā)現3的倍數，個位數與十位數相加的得數可以被3整除.

師：這一發(fā)現是否具有普遍規(guī)律呢？讓我們代入一下看看.

生：以14為例，1+4=5，5÷3=1……2，14÷3=4……2，由此可以證明發(fā)現的數學規(guī)律具有普遍性.

這樣，教師通過觀察圖示內容并組織師生對話激活學生的抽象思維、邏輯推理思維等，引導學生發(fā)現數學規(guī)律所在，確定“3的倍數的特征是各個數位上的數字之和是3的倍數，這個數就是3的倍數”這一概念，避免學生形成依賴心理.

三、基于小學數學概念教學中數形結合的策略應用反思

（一）應靈活應用多種教學方法

在傳統(tǒng)教學中，教師常使用注入式教學方法開展教學工作.教師長期使用此類教學方法容易造成學生的盲目相信、被動思考等問題，不利于學生邏輯、抽象、建模等思維的發(fā)展.長此以往，學生的思維能力得不到提升，自然無法深入理解抽象的數學概念.要避免此類教學問題的出現，教師需要創(chuàng)新教學方法.在應用數形結合思想開展教學工作時，教師應當關注學生的個人發(fā)展需要，同時結合各類科學教育理論應用不同的教學方法.比如，對于缺乏對數學概念研究興趣的學生，教師可根據情境認知理論的相關內容創(chuàng)設游戲情境、問題情境等多種情境，驅動學生借助情境發(fā)現數學現象，思考數學問題，使其在感悟直觀圖形的過程中對數學概念形成大致認識.再如，對于缺乏探究精神的學生，教師可采取問題教學法，通過提出問題、不斷追問與學生展開互動，使學生在思考問題的過程中保持思維的活躍狀態(tài)，從而在推理問題結果、抽象問題規(guī)律的過程中總結數學概念.

（二）應注重發(fā)揮教學評價的作用

教學評價具有檢驗、指導、管理等教學功能.教師在應用數形結合思想開展小學數學概念教學工作時，應注重發(fā)揮教學評價的育人作用，借助評價鼓勵學生持續(xù)參與到問題探究活動當中，使學生在結合圖形分析數量關系的過程中發(fā)現數學規(guī)律；借助評價指出學生的學習問題，使學生認識到自身邏輯、抽象等思維能力的不足，從而調整學習方式.

結 語

在概念教學中，教師應引導學生透過現象分析本質，從而真正理解相關內容，實現對新知的內化吸收與靈活應用.綜上，教師有必要將數形結合思想應用于教學工作當中，以此降低概念教學內容的難度，拉近學生與新知的距離，使學生在潛移默化的過程中形成概念表象，最終實現對相關內容的深度學習.

【參考文獻】

[1]蘇麗.數形結合：小學數學教學的一把金鑰匙[J].教育界，2022（36）：32-34.

[2]顧晨.淺談數形結合在小學數學課堂教學中的應用[J].讀寫算，2022（36）：117-119.

[3]唐曉梅.小學低年級數學教學中如何滲透數形結合思想[J].數學學習與研究，2022（35）：36-38.