某DHT車輛能量管理控制策略逆向優化方法研究

摘要：針對某在研DHT混動專用變速箱多擋位多模式的結構特征，提出了與控制判斷層級方向相反的能量管理策略優化方法。從底層控制量開始進行優化，更上一層的優化采用下層優化的結果。基于最小功率損失、最小等效比油耗等原則優化各模式下的扭矩分配，基于最優扭矩分配優化結果進行擋位優化。借助遺傳算法和解耦優化得到的各模式下的最優扭矩分配和擋位匹配，優化各模式之間的切換邊界。利用MATLAB/Simulink平臺搭建整車及控制策略模型，對結果進行驗證。仿真結果表明，基于優化得到的控制策略使得各系統運行狀態合理，且可有效地改善CS模式下的油耗水平，相關結果可作為工程應用參考。

關鍵詞：混動專用變速箱；能量管理策略；等效比油耗；模式切換；遺傳算法

中圖分類號：U461? 收稿日期：2024-04-20

DOI：1019999/jcnki1004-0226202406010

1 前言

根據國家節能與新能源汽車技術路線圖20，2035年汽車全面實現電動化，混合動力乘用車百公里油耗目標40 L/100 km[1]。混動專用變速箱（Dedicated Hybrid Transmission，DHT）由于其結構簡單、重量輕、能最大限度利用發動機高效區間，且適用插電式混合動力汽車（plug-in hybrid electric vehicle，PHEV）和混合動力汽車（hybrid electric vehicle，HEV）車型等優點，受到各主機廠和供應商青睞。

簡單的混合動力架構中，工作模式和擋位較少，動力傳輸路徑容易統一描述，利用動態規劃（dynamic programming，DP）等優化算法[2-5]進行離線優化或規則提取的工作量少。李婕等[6]借助免疫遺傳算法對P2并聯式架構的傳動系統參數和控制策略門限值進行了優化。Theo Hofman等[7]借助DP算法比較了并聯式P2、P3與P2/P3切換式三種架構的燃油經濟性與二氧化碳排放量，優化變量為電池放電量和變速器的擋位。

目前市場開發的DHT方案，從單擋位到多擋位，單電機到多電機，功率分流到扭矩解耦，動力源多、傳遞路徑復雜，與傳統混合動力架構存在本質區別，對能量管理策略也提出了更高的要求。考慮所有控制變量的優化算法工作量大，優化時間長，在DHT上工程應用性差。

本文結合某在研的DHT架構進行能量管理策略的優化，提出了與控制判斷層級方向相反的能量管理策略優化方法。基于最小功率損失、最小等效比油耗等原則優化各模式下的扭矩分配，基于最優扭矩分配優化結果進行擋位優化，再基于遺傳算法，對各模式的切換邊界進行優化，最后進行仿真驗證。

2 DHT混動架構及整車參數

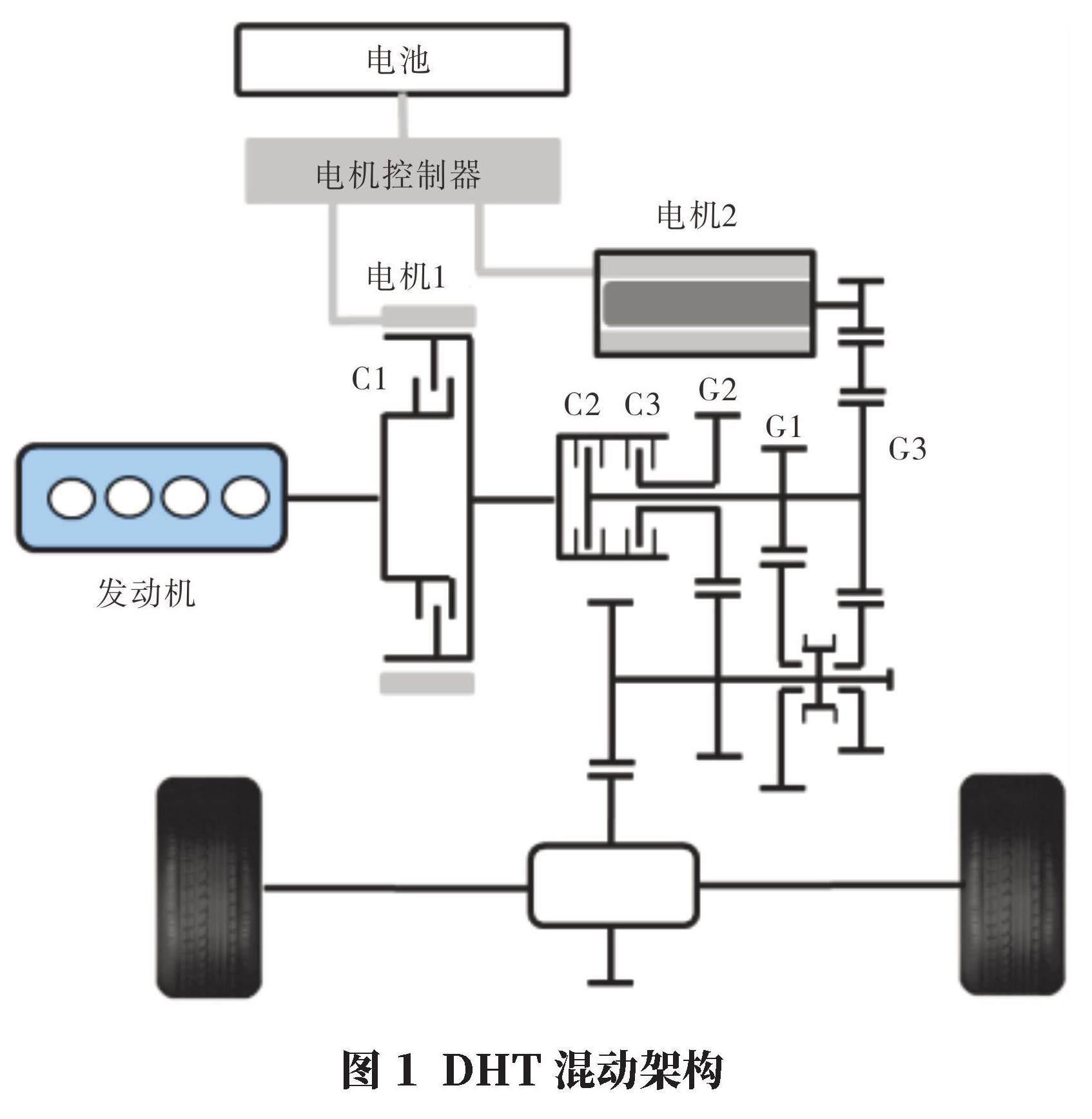
本文的研究對象為采用DHT架構的PHEV，DHT架構如圖1所示。該DHT架構包含兩個驅動電機與三個離合器，離合器C1用來實現發動機端和輪端的能量解耦，離合器C2/C3用來實現奇數擋和偶數擋的切換，同步器用來實現1-3擋位的切換；電機2通過專用齒輪連接到變速箱輸入軸。

通過不同的離合器狀態組合，該DHT可實現純電動、串聯、并聯3種動力模式，通過不同的DHT擋位組合一共能實現如表1所示的9種動力系統傳輸路徑，其中純電動模式下9種擋位組合都是有效的，并聯模式下只有其中的5種擋位有效，分別為G11、G21、G22、G23和G33，串聯模式只在G01和G03擋位有效。

該DHT架構搭載的某兩驅A級SUV車輛的整車、關鍵部件基本信息如表2所示。

3 能量管理策略逆向優化方法

DHT混動架構的能量管理策略優化時需要考慮模式、擋位和扭矩分配比例三類控制變量，三者之間相互關聯，使得優化問題十分復雜。DP算法在優化過程中，在每個工況點對模式、擋位及扭矩分配點進行耦合，DP算法的優化維度為模式個數×擋位個數×扭矩分配點個數×工況點個數。當架構的模式與擋位組合增加后，DP算法的維度呈指數變化形式，也就是通常所說的DP算法維度災難問題。且DP算法優化的結果不具備明顯的規則性，后續規則提取的工作量大。為了降低能量管理策略優化復雜度、減小規則提取工作量，同時不犧牲策略效果，提出了一種與控制判斷層級方向相反的能量管理策略優化方法。

能量管理策略在應用時依次進行模式判斷、擋位判斷和扭矩分配。本文采用的能量管理策略逆向優化方法從底層控制變量入手往上逐層優化，上層的優化采用了直接下層的優化結構，能量管理策略應用和優化時的方向如圖2所示。

本文提出的優化過程與工況解耦，只關注輪端的扭矩與車速，與DP算法相比極大地縮減了優化維度，縮減了優化時間。

4 扭矩分配與擋位優化方法

本節分別進行了三種模式下的扭矩和擋位優化，首先確定所有可能的車速工況和擋位組合下的最優扭矩分配比，再根據結果進行最優擋位匹配，最終得到所有車速工況的最優擋位匹配及對應最佳扭矩分配比。

41 純電動模式控制策略優化

411 基于最小功率損失的優化策略

純電動模式驅動過程中的功率損失發生在兩個電機和DHT變速箱部分，定義任意時刻純電動模式下的總功率損失為：

[PEVnw，Tw，iEV，αEV=Pm1l+Pm2l+PDHTl]??????????? （1）

式中，[nw]為車輪端轉速需求；[Tw]為車輪端扭矩需求；[iEV]為純電動模式下的擋位；[αEV]為電機1傳遞到車輪端的扭矩占比；[PEV]為純電動模式的總功率損失；[Pm1l]、[Pm2l]和[PDHTl]分別為電機1、電機2和DHT變速箱的功率損失。

車輪端的轉速和扭矩需求為：

[nw=30v3.6rπ]?????????????????????????????? （2）

[Tw=（Ff+Fw+Fj+Fi）r]??????????????????? （3）

式中，[v]為車速；[r]為輪胎半徑；[Ff]、[Fw]、[Fj]和[Fi]分別為滾動阻力、風阻、加速阻力和坡道阻力。

電機1、電機2傳遞到車輪端的扭矩為：

[Tm1w=TwαEV]?????????????????????????????? （4）

[Tm2w=Tw（1-αEV）]???????????????????????????? （5）

式中，[Tm1w]為電機1傳遞到車輪端的扭矩；[Tm2w]為電機2傳遞到車輪端的扭矩。

電機1、電機2和DHT變速箱的功率損失分別為：

[Pm1l=f1（nw，Tm1w，iEV）]?????????? ????????????（6）

[Pm2l=f2（nw，Tm2w，iEV）]?????????????????????? （7）

[PDHTl=f3（nw，Tw，iEV，αEV）]???????????????????????? （8）

412 扭矩分配與擋位優化

基于最小功率損失的純電動模式控制策略優化分為給定擋位的電機扭矩分配優化和基于各擋位最優扭矩分配比的擋位優化，優化問題分別描述為：

[JEV=minαEVPEVnw，Tw，iEV，αEV]?????????????????? （9）

[st.iEV∈1，9，且iEV∈N+]

[JEV=miniEVPEVnw，Tw，iEV，α*EV（iEV）]????????????? （10）

式中，[α*EV（iEV）]為當前輪端轉速、轉矩和擋位組合下的最優扭矩分配比。

對全工況點做優化，可以得到純電動模式下最優擋位及對應的最優扭矩分配比，圖3表示具體某一擋位下的最優扭矩分配比結果，圖4表示最終的最優擋位匹配結果。

純電動模式理論上9種擋位組合都有效，但由圖3給出的擋位優化結果來看，只有上述6種擋位組合屬于電能高效利用的擋位。

42 并聯模式策略優化

421 基于最小等效比油耗的優化策略

并聯模式的工作方式為發動機驅動+發電、發動機直驅和電機助力三種方式，工作方式根據發動機的發電線和排放線進行判斷，如圖5所示。

當駕駛員傳遞到發動機端的扭矩需求小于發電線扭矩時，發動機驅動的同時由電機1發電；當駕駛員的扭矩需求大于發電線扭矩且小于排放線扭矩時，發動機直接驅動，此時電機不參與驅動；當駕駛員的扭矩需求大于排放線扭矩時，發動機以排放線上的扭矩工作，剩余部分的扭矩需求由兩個電機補充，扭矩在兩個電機之間的分配按純電動模式下的最小功率損失為目標進行分配。并聯模式下三種工作方式的發動機的扭矩輸出占駕駛員轉矩需求傳遞到發動機端的比例分別大于1、等于1和小于1，表示為：

[αP>1 ????發動機驅動+發電=1??????????????????? 發動機直驅<1???????????????????????? 電機助力]??????????????? （11）

式中，[αP]為優化變量，取值范圍為[05，2]。

并聯模式下發動機為主要驅動部件，電機輔助發動機使其工作在更加高效的區間。為了統一對比三種工作方式的燃油效率，引入等效比油耗的概念，將電量消耗等效為發動機比油耗[8]。比油耗是衡量發動機燃油經濟性的一個重要指標，表示為：

[Qf=mf./Pe]?????????????? ?????????????????（12）

式中，[Qf]為比油耗，[g/kWh]；[mf.]為燃油消耗率，[g/h]；[Pe]為發動機功率，[kW]。

根據圖5所示的并聯模式驅動策略，發動機的等效比油耗可表示為：

[Qe=Qf（Pd+?Pc）Pd+?Pc（iP）'??????????????? αP>1Qf????????????????????????????????????? αP=1αPQf+1-αPQSηdisηdiP???? αP<1]??????????? （13）

式中，[Qe]為等效比油耗；[Pd]為駕駛員需求功率；[?Pc]為發動機驅動+發電方式下用于電機發電的功率；[?Pc（iP）']為存儲的功率[?Pc]再次用于電驅動時的有效功率，為了便于計算，假設擋位相同；[QS]為發動機串聯發電時的最佳比油耗；[ηdis]和[ηd（iP）]分別為電池放電效率和電機驅動效率，根據放電能量和電機驅動工作點查詢效率MAP。

發動機驅動+發電方式下，駕駛員的功率需求[Pd]小于發動機的最佳工作點[Pe]，為了提高系統效率，把發動機扭矩提高到[Pe]，多余的扭矩[?Pc]用于發電，此時用于電機發電的功率為：

[?Pc=Pe-Pd]???????????????????????? （14）

[?Pc]從發電存儲再到放電驅動，存在一系列的效率損失過程，包括電機發電、電池充電、電池放電和電機驅動，最終的實際車輪端輸出扭矩為：

[?Pc（iP）'=?Pcηgηcηdisηd（iP）]?????????????? （15）

式中，[ηg]為電機發電效率；[ηc]為電池充電效率，依據各自的效率MAP查表獲得。

422 扭矩分配與檔位優化

基于最小等效比油耗的并聯模式控制策略優化分為給定擋位的發動機扭矩分配比優化和基于各擋位最優扭矩分配比的擋位優化，優化問題描述為：

[JP=minαPQenw，Tw，iP，αP]?????????????????? （16）

[st.? iP∈1，5，且iP∈N+]

[JP=miniPQenw，Tw，iP，α*P（iP）]??????????????? （17）

式中，[α*P（iP）]為當前輪端轉速、轉矩和擋位組合下的發動機最優扭矩分配比。

對全工況點做優化，可以得到并聯模式下最優擋位和發動機扭矩分配比，圖6表示具體某一擋位下的最優扭矩分配比結果，圖7表示最終的最優擋位匹配結果。

43 串聯模式優化策略

串聯模式下發動機驅動電機1發電，發動機與車輪解耦，可運行在任意工況點，電機2負責驅動且只有兩個有效擋位。發動機運行工況點要保證SOC平衡，在策略優化的前期不予考慮，因此串聯模式下只需優化電機2的擋位。

根據串聯模式電機2最小功率損失的原則，擋位優化問題描述為：

[JS=miniSPm2lnw，Tw，iS]???????????????????? （18）

式中，[iS]為串聯模式的擋位。

對全工況點做優化，可以得到如圖8所示的串聯模式最優擋位分配。

5 基于遺傳算法的模式切換優化方法

51 遺傳算法介紹

遺傳算法[9-13]（Genetic Algorithm，GA）是由Holland上世紀70年代發展起來的。它模擬達爾文的遺傳選擇進化過程，是將生物進化過程中適者生存規則與同一群染色體的隨機信息變換機制相結合的搜索算法，算法運行步驟如圖9所示。

遺傳算法分為參數編碼、種群初始化和迭代求解部分，迭代求解部分通過交叉運算、基因變異、自然選擇等步驟產生新的種群，直至達到最大迭代次數或者滿足設定的誤差最小，得到優化解。遺傳算法采用隨機運算，對搜索空間無特殊要求，無需求導，具有運算簡單、收斂速度快等優點，因此近年來有很快的發展，并在組合優化、自適應控制、機器學習等許多領域獲得應用。

52 優化問題描述

通過第3節解耦優化得到的各模式下的最優扭矩和擋位分配結果，進行模式切換優化。模式切換可描述為以[vEV]、[PS]和[PP]為設計變量，以WLTC工況電量維持（Charge sustaining，CS）模式下的燃油消耗為優化目標的優化問題，模式切換的邊界示例如圖10所示。

[vEV]為純電動—串聯模式的車速；[Ps]為純電動—串聯模式的需求功率；[Pp]為串聯—并聯模式的需求功率，模式切換優化問題描述為：

[JGA=mini=1Nmf（mi）.·?t]??????????????????? （19）

式中，[mi]為由設計變量[vEV]、[Ps]和[Pp]決定的驅動模式；[JGA]為優化目標；[N]為WLTC工況的仿真階段數目；[?t]為仿真步長。

遺傳算法優化目標的計算采用了基于MATLAB/Simulink建立的整車及控制策略模型，控制策略模塊包含基于Stateflow的模式判斷和擋位判斷模塊，能在一定程度上解決模式和擋位頻繁切換的問題。

為了保證混合動力系統在優化過程中正常穩定運行，添加了一些約束，表示為：

[30 km/h≤vEV≤80 km/h5 kW≤Ps≤43 kW0 kW≤Pp≤50 kW]?????????????????? （20）

遺傳算法的參數設置如表3所示。

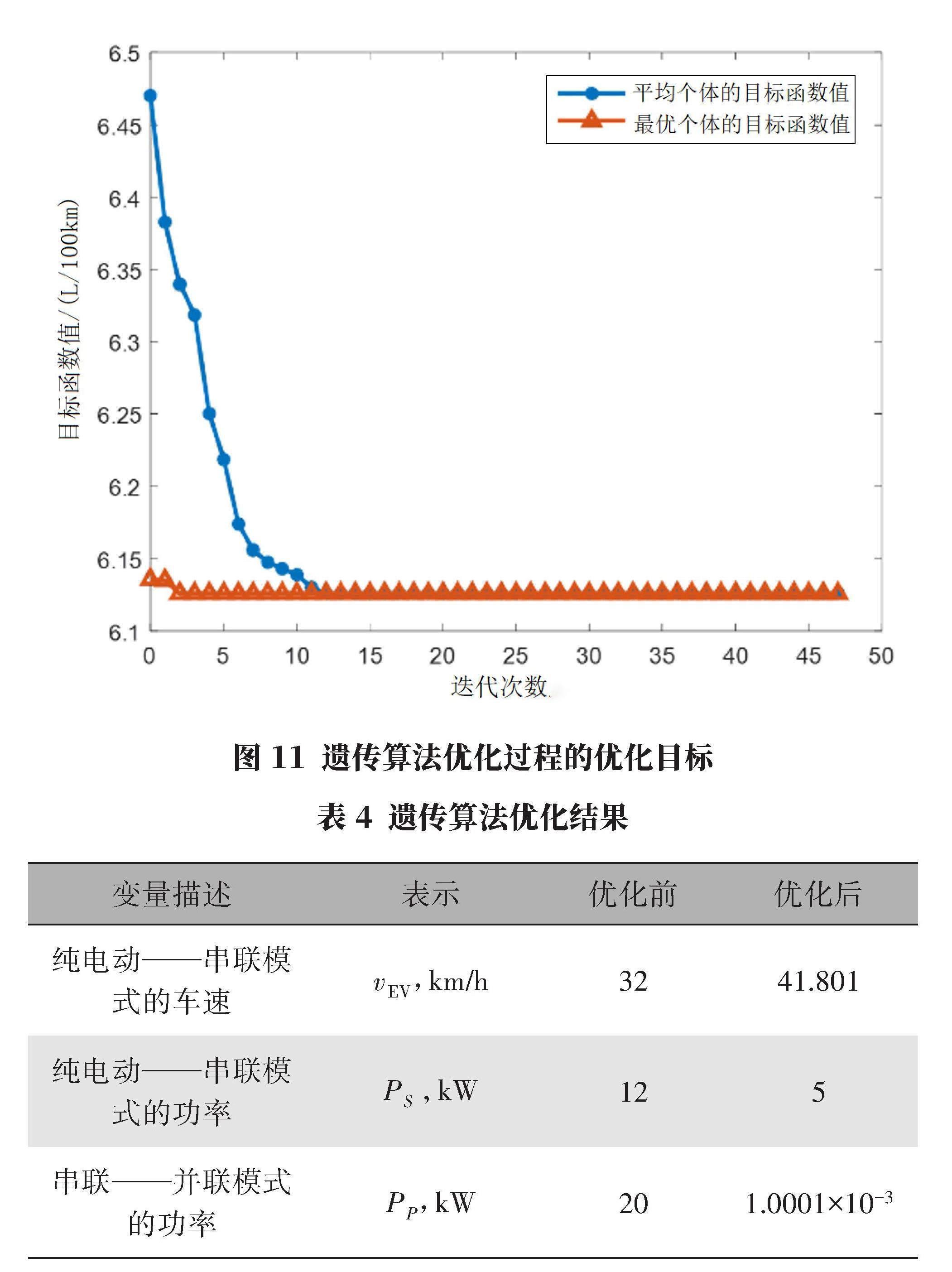
根據式（16）描述的優化問題和表4所示的遺傳算法參數，進行模式切換邊界的優化，優化過程中的各代最優及平均優化目標如圖11所示。

遺傳算法優化過程中的目標函數表明該優化算法的收斂速度快，有效節省了策略優化的時間。

遺傳算法優化后的設計變量如表4所示。

使用遺傳算法優化后的串聯—并聯模式的功率需求遠小于純電動—串聯模式的功率需求，與圖4中的示例不符。優化結果說明在本文的DHT混合動力架構下，串聯模式優勢不明顯，WLTC工況下將主要工作在純電動和并聯模式。

6 整車仿真結果對比與分析

仿真采用如圖12所示的WLTC工況，其中電量維持階段初始SOC為20%，對比了使用最優擋位和扭矩分配結果時遺傳算法優化模式切換邊界前后的結果（分別記為策略1和策略2），如表5所示。

SOC平衡由優化串聯模式的發電功率來保證。由表5可知，遺傳算法優化能節省燃油消耗84%，但相比DP算法仍有提升空間，因為DP優化算法屬于全局優化算法，考慮了前后工況之間的關系，相比策略1能節省127%的燃油消耗。

圖13、圖14分別給出了兩種控制策略下的SOC曲線和模式運行結果。圖14中綠色區域代表純電動模式，洋紅色區域代表串聯模式，橙色區域并聯模式。

圖13所示三種控制策略的SOC的始末值變化量在可接受范圍內，認為仿真的SOC前后平衡。策略1的SOC曲線在仿真開始車速較低時SOC上升，其余部分與策略2的曲線走勢高度一致。策略2相比策略1，曲線上下變化的幅度更小，減少了能量的二次轉化損失。

由圖14可知，三種策略在仿真后半部分的并聯工作區域基本一致，表明在中高車速時適合以發動機工作為主。策略1的串聯模式占比明顯高于其余兩種策略，根據遺傳算法優化結果來看，本文的DHT架構串聯工作模式并不占優勢，因此策略1的模式切換邊界并不能提供很好的整車經濟性。策略2相比于DP策略，并聯模式的占比更高，主要體現在仿真的中間部分。結合圖13的SOC曲線，仿真后半部分策略2的曲線整體波動幅度小于DP策略，策略2以并聯模式的發動機直驅方式為主，DP策略以并聯模式的電機助力方式為主，結合仿真中間部分的工作模式，DP策略能更好地發揮電池的儲能優勢。

7 結語

a.針對能量管理策略優化時控制變量多維度的問題，提出了一種與控制判斷層級方向相反的能量管理策略優化方法。

b.基于最小功率損失和最小等效比油耗原則，分別優化了純電動、并聯和串聯模式下的最優擋位及扭矩分配。

c.基于各模式下的最優擋位及扭矩分配結果，借助遺傳算法優化了模式切換的邊界。

d.經過仿真驗證，所制定策略可有效的改善CS模式下的油耗水平，模式切換邊界優化后能節省燃油84%；優化得到的擋位、扭矩分配和模式切換邊界結果為實際應用提供指導。

參考文獻：

[1]中國汽車工程學會，節能與新能源汽車技術路線圖20[M].北京：機械工業出版社，2021.

[2]Lorenzo S，Simona O，Giorgio R. A Comparative Analysis of Energy Management Strategies for Hybrid Electric Vehicles[J]Journal of Dynamic Systems，Measurement，and Control，2011，133（3）：031012

[3]王慧璇基于動態規劃的Plug-in混合動力汽車能量管理策略優化研究[D]青島：山東大學，2012

[4]張博，李君，高瑩，等Plug-in混合動力汽車能量管理策略全局優化研究[J]中國機械工程，2010，21（6）：715-720

[5]Naritomo H，Yoshihiro S，Masashi，et alDevelopment of a New Two-Motor Plug-In Hybrid System[J]SAE International Journal of Alternative Powertrains，2013，2（1）：75-82

[6]李婕，李昊，趙新蕖免疫遺傳算法的混合動力汽車多目標優化[J]計算機工程與應用，2018，54（4）：237-243-262

[7]Hofman T，Ebbesen S，Guzzella LTopology Optimization for Hybrid Electric Vehicles With Automated Transmissions[J]IEEE Transactions on Vehicular Technology，2012，61（6）：2442-2451.

[8]楊亞娟，趙韓，姜建滿，等基于效率最優的混聯式混合動力驅動系統轉矩分配研究[J]中國機械工程，2013，24（17）：2408-2413

[9]樂文峰遺傳算法在混合動力汽車能量管理策略及匹配優化中的應用[D]上海：同濟大學，2007

[10]徐群群，宋珂，洪先建，等基于自適應遺傳算法的增程式電動汽車能量管理策略優化[J]汽車技術，2012（10）：19-23

[11]張昕，張欣，田毅，等基于混合遺傳算法的HEV控制策略優化[J]汽車工程，2012，34（4）：292-296+300

[12]楊章林，朱燁，賈會星基于遺傳算法的并聯式混合動力汽車控制策略優化[J]湖南城市學院學報（自然科學版），2019，28（3）：54-57

[13]趙勇，謝金法，時佳威，等基于遺傳算法優化支持向量機工況識別的燃料電池混合動力汽車能量管理策略[J]科學技術與工程， 2020，20（14）：5820-5827

作者簡介：

張平平，男，1984年生，工程師，研究方向為汽車電控系統算法設計。