跨章節一題多解，實現知識互聯

［摘 要］ 跨章節一題多解，相較于章節內的一題多解，在提升解題能力的同時，借助思維導圖又能更好地實現知識互聯，以及在一定程度上實現各章節知識融合，從而建立立體化的知識體系.

［關鍵詞］ 一題多解；章節融合；思維導圖；知識互聯；知識立體化

跨章節一題多解問題的提出

一題多解，顧名思義是指一個問題可以有多種思路和方法來解決. 一題多解的意義在于：培養學生創造性思維；提高學生解決問題的能力；滿足不同學生的需求；幫助教師更好地了解學生的思考方式和學習情況，從而更好地指導學生學習.

但是在日常教學過程中，我們所接觸的一題多解大多是在同一章節知識體系內展開的不同思路或運算細節的處理，學生的認知結構中，各個章節各個方法相對孤立，缺乏比較和連接，于是不容易建立良好的數學方法結構，也就不容易培養數學理解能力. 相較之下，如果能夠提升跨章節一題多解的能力，利用不同章節里的知識從不同角度解決同一個問題，那么這將有利于學生綜合能力的提高，從而促進學生再認識已有知識和方法，改進和優化思維過程，使得方法理解向深度和廣度拓展，實現知識立體化，獲得更深刻、更有廣度的數學知識結構體系，最終有效提升數學學科核心素養.

1. 跨章節一題多解的難點

跨章節一題多解的難點如下：

第一，知識面覆蓋廣. 跨章節一題多解通常需要運用多個知識點，這要求學生掌握廣泛的知識，而不僅僅是某一章節的知識.

第二，抽象度較高. 一些跨章節一題多解的問題可能涉及抽象度較高的概念或原理，需要學生有一定的抽象思維能力.

第三，思維更發散. 這需要學生具有創造性思維和發散性思維，能夠從不同角度出發尋找解決方法.

第四，綜合應用難度高. 跨章節一題多解的問題通常需要學生綜合運用多個知識點和技能來解決，這要求學生具有良好的綜合應用能力和分析問題的能力.

第五，需要學生具備較強的獨立思考和探索能力，這對于一些學生來說比較困難.

因此，要讓學生真正掌握跨章節一題多解的能力，需要在教學中注重知識面的廣度、抽象思維能力的培養、發散思維和綜合應用能力的訓練，并且善于鼓勵學生獨立思考、探索和創造.

2. 思維導圖對跨章節一題多解的幫助

思維導圖是提高跨章節一題多解能力的有效工具之一，具體表現在以下幾個方面.

（1）思維導圖可以幫助學生梳理知識點，將知識點按照邏輯關系進行組織，使得學生能夠清晰了解知識點之間的關系. 這有助于學生對多個知識點進行整合，并提高學生跨章節一題多解的能力.

（2）思維導圖通過分支和節點的形式，展示問題的多個方面和不同的求解思路，可以促進學生發散性思維的發展. 學生可以通過思維導圖自由發揮思維能力，提出多種可能的解決方案和思路，培養創造性思維.

（3）思維導圖可以幫助學生綜合應用知識，提升學生的綜合應用能力. 學生可以將不同的知識點在思維導圖上進行組合和搭配，以達到解決問題的目的.

（4）思維導圖可以幫助學生回顧、總結和反思學習過程，自我檢查和評估所掌握的知識和技能，發現自己的不足之處，并不斷補充和改進.

案例探究

下面以一個例題為出發點，充分挖掘題設條件中所能提供的信息，借助思維導圖，嘗試建立每一種可能的解題思路與相應章節知識的聯系，舉行一場思維盛宴. 例題如下：“如圖1所示，在△ABC中，點D在邊BC上，且BD=2DC，∠BAC=90°，AD=1，則線段CD長度的范圍是______.”

1. 解題指導

羅增儒教授的《數學解題學引論》中有這樣一個解題坐標系［1］：如圖2所示，條件中能想到的信息組成一個“同心圓”，目標結論所需要的條件信息組成另一個“同心圓”，尋找解題思路的過程就是通過分析思考擴大兩個圓的范圍直至找到“交點”，最終的路徑可以是很多個，這就形成了一題多解. 一方面，每一種方法都可以再進一步思考是否可以優化；另一方面，不同方法之間并不一定有“優劣”之分，只是用到了不同分支甚至是不同章節的知識. 我們要珍惜這種思維碰撞，這對促進知識融合和提高綜合解題能力有極大的幫助.

2. 嘗試發散思維

我們試著以思維導圖的形式分析本題條件所關聯的知識點，請看圖3和圖4.

通過思維發散，圖3和圖4充分列舉了題目條件所關聯的在整個高中數學章節范圍內的知識點，以及到達目標有可能通過的路徑，其中包含解析幾何、向量、函數、不等式、三角函數等章節的知識點. 這樣一來，圖2所示的兩個“同心圓”就準備到位了，接下來要做的就是尋找兩個同心圓的“交點”，即充分挖掘圖3和圖4所述的知識點之間的聯系——捕捉有用的信息，通過觀察和分析發現隱蔽關系，建立條件和結論之間的有機聯系，進而從不同角度尋找解決問題的方法，形成不同的解題路徑.

3. 整合思路，形成解題過程

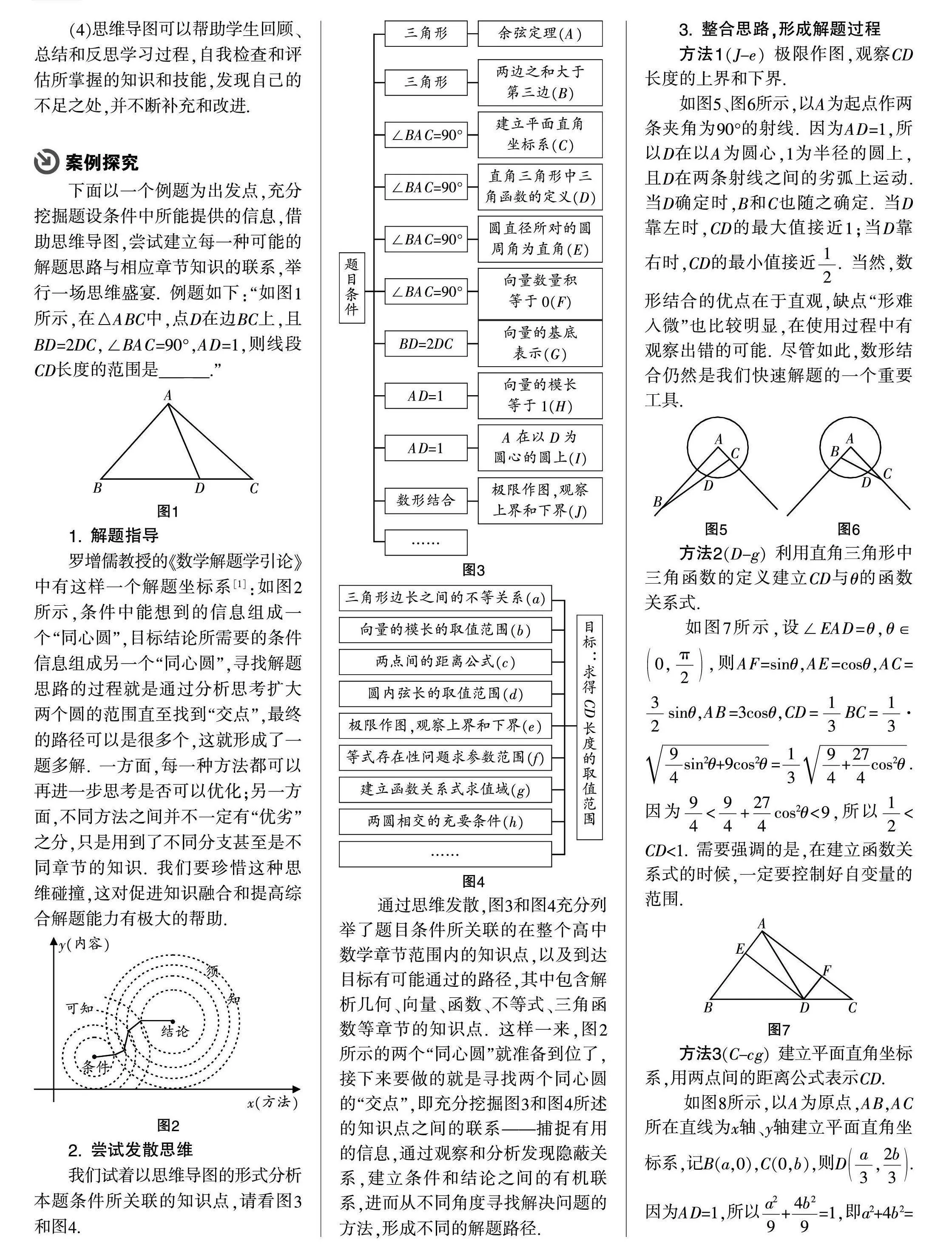
方法1（J-e） 極限作圖，觀察CD長度的上界和下界.

如圖5、圖6所示，以A為起點作兩條夾角為90°的射線. 因為AD=1，所以D在以A為圓心，1為半徑的圓上，且D在兩條射線之間的劣弧上運動. 當D確定時，B和C也隨之確定. 當D靠左時，CD的最大值接近1；當D靠右時，CD的最小值接近. 當然，數形結合的優點在于直觀，缺點“形難入微”也比較明顯，在使用過程中有觀察出錯的可能. 盡管如此，數形結合仍然是我們快速解題的一個重要工具.

方法2（D-g） 利用直角三角形中三角函數的定義建立CD與θ的函數關系式.

如圖7所示，設∠EAD=θ，θ∈

0，

，則AF=sinθ，AE=cosθ，AC=sinθ，AB=3cosθ，CD=BC=·=.因為<+cos2θ<9，所以<CD<1. 需要強調的是，在建立函數關系式的時候，一定要控制好自變量的范圍.

方法3（C-cg） 建立平面直角坐標系，用兩點間的距離公式表示CD.

如圖8所示，以A為原點，AB，AC所在直線為x軸、y軸建立平面直角坐標系，記B（a，0），C（0，b），則D

，

. 因為AD=1，所以+=1，即a2+4b2=9，所以CD==. 由a2>0，

b2>0得0<b2<，所以<CD<1. 需要強調的是，在代入消元時，被消的元的取值范圍要傳遞給新元.

方法4（A-f） 利用余弦定理建立CD與某直觀變量之間的等量關系.

如圖9所示，設CD=x，則cosC=，cosC=. 根據數學中“算兩次”的思想，可得=，整理得3-3x2=AC2. 又0<AC<3x，所以0<3-3x2<9x2，解得<x<1. 需要強調的是，利用等式存在性求其中一個變量的取值范圍時，要控制好其他變量的取值范圍.

方法5（G-g） 以，為基底表示，從而求模長范圍.

如圖10所示，記=a，=b，因為BD=2DC，所以=a+b. 因為

=1，所以a2+4b2=9，所以

=（b-a）==. 下同方法3.

方法6（F-f） 借助·=0，建立與已知長度的的等量關系.

如圖11所示，記=a，=b，a，b的夾角為θ，CD=

b

=t. 因為·=0，所以（a-2b）（a+b）=0，化簡得1-tcosθ-2t2=0，即cosθ=. 注意到θ∈（0，π），則cosθ∈（-1，1），所以-1<<1，解得<t<1.

方法6與方法4類似，利用等式存在性求某個變量的取值范圍，需要一定的知識儲備，這里匯集了解不等式、求值域和函數零點等知識點. 學生在日常學習中要注重知識的積累和總結，以及對方法的優化和反思. 相關拓展可參考文［2］.

方法7（B-a） 構造三角形，利用兩邊之和大于第三邊的基本關系列不等式.

如圖12所示，取BC的中點E，連接AE，設DE=x，則AE==3x. 又AD=1，在三角形ADE中，有x+1>3x，

x+3x>1，

3x+1>x，解得<x<，CD=2x，所以<CD<1.

方法8（EI-h） 點A同時位于兩個隱藏的圓上，利用兩圓相交的充要條件列不等式.

如圖13所示，一方面，點A在以D為圓心，1為半徑的圓上；另一方面，點A在以BC為直徑的圓上. 借助兩圓相交的充要條件可得

1-CD<CD<1+CD，解得<CD<1.

方法9（E-d） 挖掘出一個深度隱藏的圓，在該圓內觀察CD長度的范圍.

如圖14所示，過C作AC的垂線，交AD的延長線于點E，取AE的中點O，則∠ACE=90°. 根據三角形相似可知==，所以DE=. 所以，點C在以AE為直徑的圓O上，從而DE<CD<AD，即<CD<1.

在方法8和方法9中，都用到了“隱藏圓”，這需要學生在日常學習中多思考、多發現、多總結、多概括，這些都是思維的基礎，豐富的知識模塊會帶來正向的思維定式，思維的敏捷性和發散性都能得到極大的提高. 與“隱藏圓”相關的拓展可參考文［3］.

結語

要培養學生跨章節一題多解的能力，就要注重培養學生創造性思維、綜合應用能力和自主學習能力等. 通過提供多種不同類型的問題、組織跨學科知識梳理、增加可供聯想的解題過程，引導學生分析問題本質，從而幫助學生掌握跨章節一題多解的能力，提高學生的綜合素質和解題能力.

跨章節一題多解可以幫助實現整個學科知識的互聯，再進一步，就是跨學科知識融合，教師可以嘗試將不同章節甚至不同學科的知識點組織起來，設計相關問題，引導學生綜合分析和解決問題，從而建立立體化的知識體系.

參考文獻：

［1］ 羅增儒. 數學解題學引論［M］. 西安：陜西師范大學出版社，2016.

［2］ 李忠良. 從一類含參等式存在性問題看“范圍的傳遞”［J］. 中學數學月刊，2016（04）：39-40 .

［3］ 李忠良. 尋找一些隱藏著的圓［J］. 中學數學教學參考，2017（28）：36-38.