基于反相器和開關架構的低復雜度混合預編碼方案

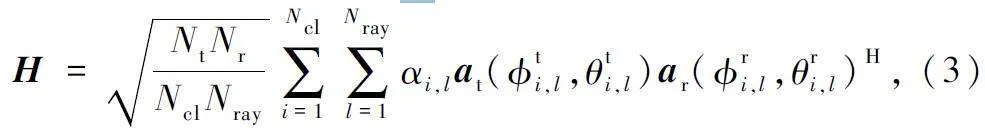
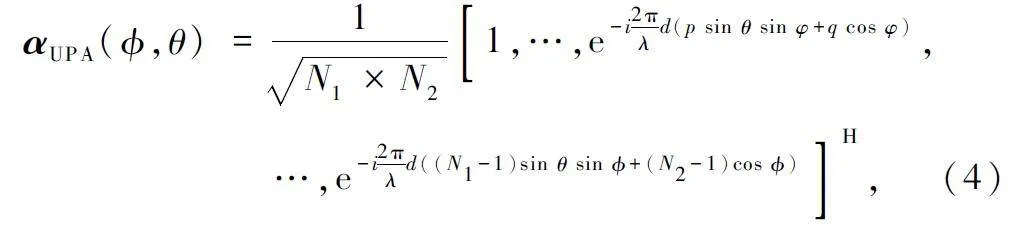
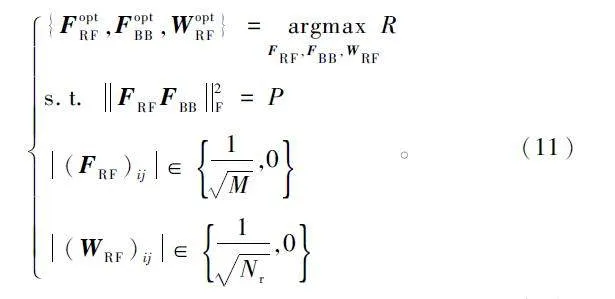
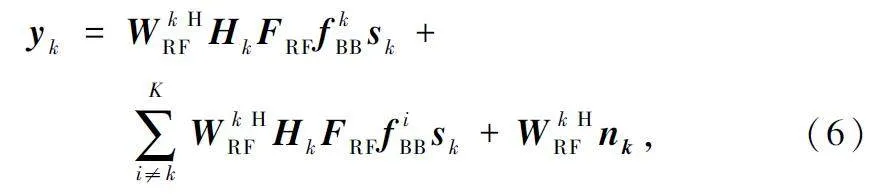
摘 要：采用有少量反相器和開關（Ｉｎｖｅｒｔｅｒ ａｎｄ Ｓｗｉｔｃｈ，ＩＳ）組合的預編碼架構設計模擬預編碼部分，相比傳統移相器結構的混合預編碼可以有效降低系統功耗。利用此結構的混合預編碼在計算收發端最優的編碼矩陣時會變成一個求解復雜的離散組合問題。針對多天線多用戶的毫米波大規模多輸入多輸出（Ｍｕｌｔｉｐｌｅ Ｉｎｐｕｔ Ｍｕｌｔｉｐｌｅ Ｏｕｔｐｕｔ，ＭＩＭＯ）場景，提出了一種新的優化方案———ＳＶＤ＿ＣＥ，可將２ 個矩陣的聯合優化問題轉化為２ 個獨立的組合優化問題，基于改進交叉熵（Ｃｒｏｓｓ Ｅｎｔｒｏｐｙ，ＣＥ）算法分別求解編解碼矩陣。仿真結果表明，所提方案與已有解決方案相比不會造成系統性能的損失，在取得相同性能時利用ＣＥ 算法中所需候選集的數量大幅減少，有效降低了求解的復雜度。

關鍵詞：毫米波；大規模多輸入多輸出；混合預編碼；交叉熵算法；奇異值分解

中圖分類號：ＴＮ９２９． ５ 文獻標志碼：Ａ 開放科學（資源服務）標識碼（ＯＳＩＤ）：

文章編號：１００３－３１０６（２０２４）０５－１２４７－０８

０ 引言

毫米波大規模多輸入多輸出（Ｍｕｌｔｉｐｌｅ ＩｎｐｕｔＭｕｌｔｉｐｌｅ Ｏｕｔｐｕｔ，ＭＩＭＯ）在５Ｇ 中的廣泛應用，使其成為未來通信高性能發展的一項關鍵技術，可以通過在基站（Ｂａｓｅ Ｓｔａｔｉｏｎ，ＢＳ）端配置幾十甚至上百根發射天線來大幅度提升系統的空間分辨率，顯著提升頻譜效率和能量效率［１－２］。在傳統的ＭＩＭＯ 系統中，預編碼一般是利用數字預編碼器實現，能夠同時調整信號的大小和相位，全數字（Ｆｕｌｌｙ Ｄｉｇｉｔａｌ，ＦＤ）預編碼中每根天線都要連接一條射頻（Ｒａｄｉｏ Ｆｒｅ-ｑｕｅｎｃｙ，ＲＦ）鏈路［３］。如果按照傳統ＭＩＭＯ 系統的純數字預編碼方案來設計天線數量劇增的大規模ＭＩＭＯ 系統，需要大量ＲＦ 鏈路，會導致巨大的系統硬件設計復雜度和超大功耗。為了減少系統所需的ＲＦ 鏈數量，混合預編碼技術被深入研究。這種混合結構也可以大大消除多用戶數據流之間的干擾以提升系統性能［４］。目前混合預編碼研究主要分為全連接和部分連接２ 種不同類型的系統結構。

全連接結構即每條ＲＦ 鏈路都可以連接到所有發射天線，為ＲＦ 鏈路提供完整的波束形成增益。文獻［５－８］針對全連接結構，提出不同混合預編碼算法，保證系統可取得接近最優純數字預編碼方案下的性能，但是全連接結構由于硬件設計復雜，系統功耗損失嚴重，導致系統能量效率較低。部分連接結構，每條ＲＦ 鏈路僅連接部分天線，通過犧牲部分波束增益來降低系統的功耗。文獻［９ －１０］針對部分連接結構提出不同的優化方案，相比全連接混合預編碼，系統性能有所損失，但是在系統能效上有更優的表現。為避免部分連接結構在降低系統功耗時所帶來的系統天線陣列的增益損失問題。文獻［１１－１３］提出根據信道環境變化完成發射天線與ＲＦ 鏈路的最優自適應連接方案，可以有效降低系統性能的損失。在大規模ＭＩＭＯ 中，利用高分辨率移相器（Ｐｈａｓｅ，ＰＳ）組成的混合預編碼結構，即使采用部分連接，仍存在較大的功耗和硬件設計問題。文獻［１４］提出一種使用反相器和開關（Ｉｎｖｅｒｔｅｒ ａｎｄＳｗｉｔｃｈ，ＩＳ）相結合的預編碼結構，避免了ＰＳ 造成的功耗問題，但是ＩＳ 架構限制了模擬預編碼部分可選的相位為｛０，π｝，所以對模擬預編碼和數字預編碼矩陣的求解過程就變成了一個離散的組合優化問題。文獻［１４］在單用戶場景下，提出基于ＣＥ 算法改進的ＡＣＥ 算法，依據每個開關相位取值的概率分布同時優化整個模擬預編碼矩陣，尋找最優解。文獻［１５］在文獻［１４］的基礎上按照逐個優化每個ＩＳ 取值的思想提出基于廣義空間調制輔助的坐標更新算法（Ｃｏｏｒｄｉｎａｔｅ Ｕｐｄａｔｅ Ａｌｇｏｒｉｔｈｍ，ＣＵＡ）。文獻［１４－１５］只解決了單用戶系統中的發送端預編碼矩陣的組合優化問題，所提出的算法無法有效擴展到多天線多用戶場景中。

針對上述問題，本文在ＩＳ 架構的基礎上，重點針對多天線多用戶的場景，假設已知信道狀態信息（Ｃｈａｎｎｅｌ Ｓｔａｔｅ Ｉｎｆｏｒｍａｔｉｏｎ，ＣＳＩ）的前提下，提出一種基于信道奇異值分解（Ｓｉｎｇｕｌａｒ Ｖａｌｕｅ Ｄｅｃｏｍｐｏｓｉｔｉｏｎ，ＳＶＤ）與交叉熵聯合的優化的算法。算法利用發送端的模擬預編碼矩陣與接收端的組合接收矩陣間的關聯性，通過信道的ＳＶＤ，將２ 個矩陣的聯合優化問題轉化為２ 個獨立的優化問題，然后分別利用ＣＥ算法進行２ 個矩陣的最優求解。為進一步在部分連接方案下提高系統性能，本文加入天線動態分配的機制，設計同時降低功耗和保持系統增益的改進方案。仿真結果表明，本文所提出的算法在多用戶場景中可有效降低離散組合求解的復雜度，且不會造成系統的額外性能損失，而利用動態的連接方案亦可進一步提高系統的性能。

１ ＩＳ 系統模型

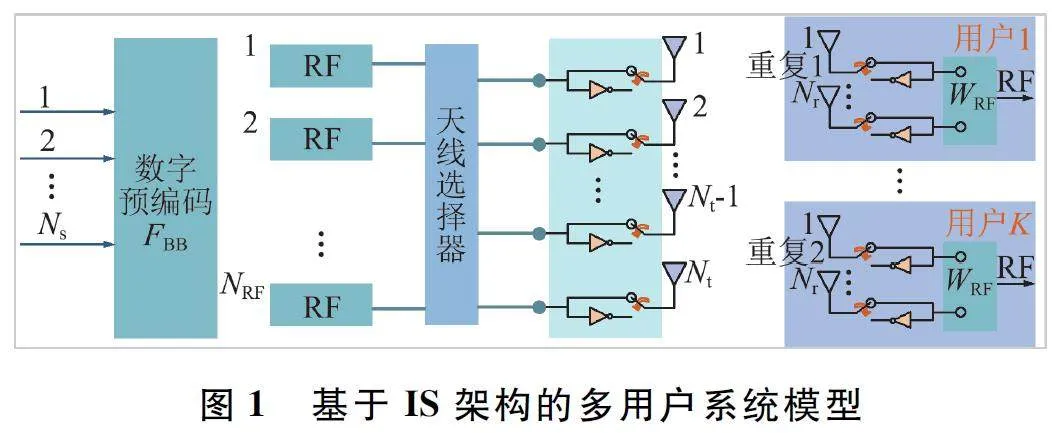
考慮一個服務于多用戶的毫米波大規模ＭＩＭＯ系統，如圖１ 所示。在該系統模型中發送數據流數為Ｎｓ，發送ＲＦ 鏈路數為ＮＲＦ，ＢＳ 端配置Ｎｔ 根發射天線，該系統服務于Ｋ 個用戶終端，假設每個用戶終端都配置Ｎｒ 根接收天線和一條接收ＲＦ 鏈路。

為了使系統完全實現多路復用增益［１６］，假定發送數據流數Ｎｓ、發送ＲＦ 鏈路ＮＲＦ 相等。

圖１ 的系統中，由于模擬預編碼部分通過ＩＳ 器件組合而成，導致ＦＲＦ 矩陣與采用ＰＳ 的模擬預編碼矩陣有所差異，并且對應的模擬預編碼器的約束條件也不相同。為了在部分連接的結構中提高系統性能，本文根據ＣＳＩ 給每條ＲＦ 鏈路選擇較優的部分天線陣列，模擬編碼矩陣可表示為ＦＲＦ ＝ ［ｆＲＦ１ ，ｆＲＦ２ ，…，ｆＲＦＮＲＦ］∈CＮｔ×ＮＲＦ，ｆＲＦｋ ∈CＮｔ×１ 。假設每條ＲＦ 鏈路均等分配Ｍ ＝ Ｎｔ ／ ＮＲＦ 根互不相同的發射天線，則對于每一個ｆＲＦｋ 向量，僅有Ｍ 個非零元素組成，ＦＲＦ編碼矩陣中總共僅有 Ｎｔ 個屬于集合 １ ／槡Ｍ｛－１，１｝非零元素。

對于用戶接收端，需要采用模擬組合器對接收到的信號進行處理，所以對于每個用戶來說模擬組合接收矩陣為ＷｋＲＦ ∈CＮｒ×１ ，同時本文考慮接收端的模擬組合部分和ＢＳ 發送端模擬部分采用相似的系統結構，所以其組成元素集合為１ ／ 根號下Ｎｒ ｛－１０，１０｝。根據以上系統模型可以得到ＢＳ 端發送信號ｘ 可表示為：

ｘ ＝ ＦＲＦ ＦＢＢ ｓ， （１）

式中：ｓ ＝ ［ｓ１ ，ｓ２ ，…，ｓＮｓ］ Ｔ 為Ｎｓ 個數據流傳輸的信號矢量，且滿足Ε［ｓｓＨ ］＝ ＩＮｓ；ＦＢＢ ∈CＮＲＦ×Ｎｓ為數字預編碼矩陣，ＦＲＦ 為模擬預編碼矩陣，并且二者需要滿足恒定傳輸功率約束， ||ＦＲＦ ＦＢＢ||２Ｆ ＝ Ｐ，Ｐ 為系統傳輸功率。在組合接收之前用戶ｋ 的接收信號可以表示為：

ｙ ＝ Ｈｋ ＦＲＦ ＦＢＢ ｓ ＋ ｎｋ ， （２）

式中：Ｈｋ ∈CＮＲＦ×Ｎｓ為ＢＳ 端與用戶ｋ 之間的信道矩陣，ｎｋ 為用戶ｋ 接收到的噪聲干擾向量，服從均值為０、方差為δ２ 的復加性高斯白噪聲。對于多用戶系統信道矩陣可表示為Ｈ ＝ ［ＨＴ１ ，ＨＴ２ ，… ，ＨＴＫ］ Ｔ ∈CＮｒ×Ｋ×Ｎｔ。

對于毫米波大規模ＭＩＭＯ 系統的無線信道建模，本文采用基于擴展的Ｓａｌｅｈ-Ｖａｌｅｎｚｕｅｌａ［６］毫米波信道模型，其信道矩陣Ｈ 如下：

式（３）表示該信道模型具有Ｎｃｌ 個散射簇，每個散射簇包含有Ｎｒａｙ 條傳輸路徑，αｉ，ｌ 為第ｉ 個散射簇中第ｌ 條路徑的增益，且服從ＣＮ ∈ （０，σ２αｉ ），σ２αｉ 為第ｉ 個散射簇的平均功率。ａｔ（Φｔｉ，ｌ，θｔｉ，ｌ ）和ａｒ（Φｒｉ，ｌ，θｒｉ，ｌ）為發射端和接收端中隨方位角變化的天線陣列響應矢量，其中Φｔｉ，ｌ 和θｔｉ，ｌ 為發送端的水平和垂直出發角（Ａｎｇｌｅ ｏｆ Ｄｅｐａｒｔｕｒｅ，ＡｏＤ），Φｒｉ，ｌ 和θｒｉ，ｌ 為接收端的水平和垂直到達角（Ａｎｇｌｅ ｏｆ Ａｒｒｉｖａｌ，ＡｏＡ）。假設收發兩端都采用均勻平面陣列（Ｕｎｉｆｏｒｍ ＰｌａｎａｒＡｒｒａｙ，ＵＰＡ），對應的ＵＰＡ 響應矢量可以表示為：

式中：Ｎ１ 和Ｎ２ 為ＵＰＡ 天線陣列在水平和垂直方向的分布數量，０≤ｐ≤Ｎ１ －１，０≤ｑ≤Ｎ１ －２；ｄ 為天線間距，λ 為信號波長，為了便于計算通常設置ｄ ＝ λ ／ ２。

假設用戶ｋ 接收到的信號為ｙｋ，用戶端通過模擬組合器Ｗ ｋＲＦ 接收后的信號可以表示為：

ｙｋ ＝ Ｗ ｋ ＨＲＦ Ｈｋ ＦＲＦ ＦＢＢ ｓ ＋ Ｗ ｋ ＨＲＦ ｎｋ 。（５）

對于用戶ｋ 接收到的信號，可以分為期望接收到的信號和其他用戶以及信道噪聲的干擾信號，則式（５）可以進一步表示為：

式中：ｆ ｋ

ＢＢ 為數字編碼矩陣ＦＢＢ 的ｋ 列。

為了方便衡量ＭＩＭＯ 系統的性能變化，采用系統和速率近似表示。通過信干噪比（Ｓｉｇｎａｌ ｔｏ Ｉｎｔｅｒ-ｆｅｒｅｎｃｅ ｐｌｕｓ Ｎｏｉｓｅ Ｒａｔｉｏ，ＳＩＮＲ）的定義，對于第ｋ 個用戶對應的量化ＳＩＮＲｋ 可以表示為：

２ 問題描述與求解方案

２． １ 目標函數

本文目的是通過復雜度較低的算法，計算最優的ＦＲＦ、ＦＢＢ 和ＷＲＦ，通過最大化系統的可達和速率Ｒ 來衡量ＩＳ 架構混合預編碼器的性能，所以目標函數為：

在式（１１）所示的目標函數中存在恒模約束條件，屬于三元聯合的非凸問題，直接求取全局最優解比較困難。而采用ＩＳ 架構的預編碼器，可以看作固定了模擬預編碼器可選擇的相位取值，但是對于大規模ＭＩＭＯ 系統，發射天線數量比較多，如果直接采用組合優化，僅ＦＲＦ 可選的組合就多達２Ｎｔ 個，計算復雜度很高。如果直接解決離散的組合優化問題，多采用機器學習的啟發式算法，文獻［１４ －１５］提出的ＡＣＥ 算法和ＣＵＡ 算法也是基于這種思想，并且這２ 種算法更適合單用戶場景。對于本文多用戶系統模型，想要同時優化模擬預編碼矩陣和組合接收矩陣并不合適。

２． ２ 解決方案

大量預編碼研究證明，利用信道矩陣可以得到最優的純數字預編碼和接收預編碼矩陣［１７－１８］，而混合預編碼中的數字預編碼和模擬預編碼可以看作分解的純數字預編碼，所以待求解的最優模擬編碼矩陣與最優的純數字預編碼之間有著很大的關系。而在本文中需要同時優化ＢＳ 端和用戶端的模擬組合矩陣，可以利用信道的ＳＶＤ 將這個問題解耦為２ 個基本獨立的組合優化問題，然后分別根據２ 個最優的純數字編碼矩陣利用ＣＥ 算法來優化ＢＳ 端的模擬預編碼矩陣和用戶端的組合接收矩陣。

２． ３ 具體的求解過程

對于多用戶場景，為了減少用戶之間的干擾，本文利用ＢＤ 預編碼求解最優的數字預編碼和組合接收矩陣。對于用戶ｋ，設Ｈ＾ ＝ ［ＨＴ１ ，…，ＨＴｋ－１ ，ＨＴｋ＋１ ，ＨＴｋ，…，ＨＴＫ］ Ｔ 為除了用戶ｋ 外其他用戶組成的信道矩陣。對于Ｈ＾ 做ＳＶＤ，可以得到：

Ｈ ＾＝ Ｕ１ Σ１ ＶＨ１ ， （１２）

式中：Ｕ１ 為左酉矩陣，Ｖ１ 為右酉矩陣，Σ１ 為信道Ｈ＾的特征值組成的對角矩陣。根據ＢＤ 預編碼，可以得到用戶ｋ 的第一預編碼矩陣Ｖｋ１ ＝ Ｖ１（：，Ｂｋ：ｅｎｄ），Ｂｋ 為Ｈ＾ 的秩。

接下來可以得到用戶ｋ 的等效矩陣為Ｈｅｆｆｋ ＝Ｈｋ Ｖｋ１ ，對于Ｈｅｆｆｋ 進行ＳＶＤ，可以得到：

Ｈｅｆｆｋ ＝ Ｕ２ Σ２ ＶＨ２ 。（１３）

根據式（１３）可以得到用戶ｋ 的第二個預編碼矩陣Ｖｋ２ ＝ Ｖ２（：，１：Ｂｅ ），Ｂｅ 為Ｈｅｆｆｋ 的秩。用戶ｋ 的最優預編碼矩陣Ｆｏｐｔ 和最優接收編碼矩陣Ｗｏｐｔ 可以表示為：

Ｆｏｐｔ ＝ Ｖｋ１ Ｖｋ２ ， （１４）

Ｗｏｐｔ ＝ Ｕ２（：，１：ＮＲＦ ）。（１５）

接下來利用Ｆｏｐｔ 和Ｗｏｐｔ，通過交叉熵算法分別優化用戶ｋ 對應的發送模擬預編碼矩陣ｆ ＲＦｋ 和接收端的組合接收矩陣Ｗ ｋＲＦ。

由于本文采用動態的部分連接方式，所以可以根據信道函數增益，為發送用戶ｋ 數據流的ＲＦ 鏈路動態的選擇部分發送天線，為了減小計算用戶候選天線的復雜度，假設每條發送ＲＦ 鏈路都分配相同數量的發射天線與之連接，即Ｍ ＝ Ｎｔ ／ ＮＲＦ。對于為每條ＲＦ 鏈路選擇所屬的Ｍ 根發射天線的過程中，為了盡量保證每個用戶的公平性，通過每次迭代分別為每個ＲＦ 鏈路選擇一根互不相同的最優天線，具體分配過程如算法１ 所示。

使用ＣＥ 算法分別求解發收端的編解碼矩陣，首先根據已知的先驗概率生成Ｓ１ 個候選的ｆ ＲＦｋ 和Ｓ２ 個候選Ｗ ｋＲＦ 向量，由于ＦＲＦ ＝ ［ｆ ＲＦ１ ，ｆ ＲＦ２ ，…，ｆ ＲＦＮＲＦ］∈CＮｔ×ＮＲＦ，對于ｆ ＲＦｋ 僅在分配給第ｋ 個ＲＦ 鏈路的Ｍ 個天線對應索引位置為非零元素，其余位置全部設置為０。在ＣＥ 算法的計算過程中，假設每次迭代中發送端對應的先驗概率ｕｔ ＝ ［ｕ１ ，ｕ２ ，… ，ｕＮ ，… ，ｕｎ ，ｕＭ ］Ｔ ∈CＭ×１ ，其中０≤ｕｎ ≤１ ，分別對應Ｍ 個非零元素取值為 １ ／根號下Ｍ 的概率。在第一次迭代循環中，假設每一個非零元素的取值 １ ／根號下Ｍ｛－１，１｝為等概率分布的，所以對于發送端的初始化先驗概率可以表示為ｕｔ ＝ ［０． ５，０． ５，…，０．５］ Ｔ ∈CＭ×１ ，對應Ｍ 個非零元素取值為 １ ／根號下Ｍ的概率，則取值為－１ ／根號下Ｍ的概率為ｕ′ｔ ＝ ｏｎｅｓ（Ｍ，１）－ｕｔ。用戶接收端與ＢＳ 發送端的ＣＥ 初始化參數類似。

在ＣＥ 算法中，最重要的步驟是需要在每次迭代中更新下一次的先驗概率，由于已經獲得了用戶ｋ 對應的Ｆｏｐｔ 和Ｗｏｐｔ，將其作為發送端和接收端對應的最優參考矩陣。

為了更準確地更新下一輪迭代的先驗概率，本文設計式（１６）和式（１７）分別計算Ｇｆ 和Ｇｗ 作為ｆ ＲＦｋ與Ｆｏｐｔ，以及ＷｋＲＦ 與Ｗｏｐｔ 的匹配度參數。

Ｇｆ ＝ |ｆ ＲＦ Ｔｋ Ｆｏｐｔ| ， （１６）

Ｇｗ ＝ |Ｗ ｋ ＴＲＦ Ｗｏｐｔ| 。（１７）

考慮到最優的Ｆｏｐｔ 和Ｗｏｐｔ 的每一列分別對應Σ２ 中的每一個奇異值，而每一個奇異值又可以衡量該奇異值在被分解矩陣中的所占比重，所以基于每一個奇異值，為Ｆｏｐｔ 和Ｗｏｐｔ 的每一列向量添加一個與奇異值對應的權重系數Ｗ ＝ Ｓｖ ／ ΣＳｖ，Ｓｖ 為奇異值組成的向量，所以式（１６）和式（１７）可以重寫為：

Ｇｆ ＝ |（ｆ ＲＦ Ｔｋ Ｆｏｐｔ）·Ｗ| ， （１８）

Ｇｗ ＝ |（Ｗ ｋ ＴＲＦ Ｗｏｐｔ）·Ｗ| 。（１９）

對所有的候選ｆ ＲＦｋ 和Ｗ ｋＲＦ，分別計算對應的Ｇｆ和Ｇｗ ，然后排序選擇匹配度最高的Ｎｅｌｉｔｅｓ 個ｆ ＲＦｋ 和Ｗ ｋＲＦ 作為本輪精英。接下來根據所選的精英ｆ ＲＦｋ 和Ｗ ｋＲＦ 的取值，計算下一輪迭代中的每個位置的先驗概率ｕｔ（ｉ＋１）和ｕｒ（ｉ＋１），經過多次迭代最終得到先驗概率分布為恒定的０ 和１ 時，對應匹配度最高的ｆ ＲＦｋ和Ｗ ｋＲＦ，分別作為第ｋ 個ＲＦ 對應的最優的模擬預編碼矩陣和第ｋ 個用戶最優的模擬組合接收矩陣。具體的ＳＶＤ＿ＣＥ 算法過程見算法１。

２． ４ 復雜度分析

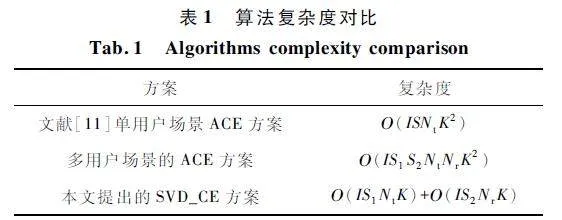
表１ 為幾種方案的復雜度對比，其中Ｉ 表示仿真中總的迭代次數，Ｓ 表示單用戶場景中每次迭代生成的候選集數量，Ｓ１ 和Ｓ２ 表示多用戶場景中每次迭代生成的模擬預編碼矩陣和接收組合矩陣的候選數量。采用ＳＶＤ＿ＣＥ 算法將需要多個矩陣聯合優化的組合問題分解為獨立的離散組合優化問題，所以每個離散組合優化的復雜度僅為Ο（ＩＳＮＫ），與ＳＶＤ算法相比大大降低了計算的復雜度，下面將通過仿真證明此結論。

３ 仿真結果分析

為了驗證本文所提算法的有效性，分別對比最優的ＦＤ 預編碼方案、文獻［１９］中基于匹配正交追蹤（Ｏｒｔｈｏｇｏｎａｌ Ｍａｔｃｈｉｎｇ Ｐｕｒｓｕｉｔ，ＯＭＰ）的全連接混合預編碼、多用戶場景中文獻［１２］的ＡＣＥ 方案和加入動態分配的部分連接的ＡＣＥ 方案，以及本文提出的動態部分連接的ＳＶＤ＿ＣＥ 方案的多個性能指標。為更方便在仿真圖中表示幾種算法，使用ＡＣＥ１ 代表多用戶場景中加入動態分配的部分連接方案，ＡＣＥ２代表文獻［１２］中固定子連接的部分連接方案，ＳＶＤ＿ＣＥ 代表本文提出的算法。

３． １ 系統和速率分析

不同信噪比（Ｓｉｇｎａｌ ｔｏ Ｎｏｉｓｅ Ｒａｔｉｏ，ＳＮＲ）下系統和速率如圖２ 所示，系統仿真的參數設置為Ｋ ＝ＮＲＦ ＝ Ｎｓ ＝ ８，Ｎｔ ＝ １４４，Ｎｒ ＝ ４。在不同ＳＮＲ 下，分別計算了幾種方案下系統的可達和速率的變化情況，在ＡＣＥ 方案中Ｓ１ ＝ １２０，Ｓ２ ＝ １００ 并迭代１５ 次。由圖２可以看出，動態連接的ＳＶＤ＿ＣＥ 和ＳＶＤ１ 方案對比文獻［１１］的ＡＣＥ２ 方案，在相同的參數下明顯提高了系統性能。此時利用所提出的ＳＶＤ＿ＣＥ 算法，僅需要在迭代１０ 次的情況下，分別利用Ｓ１ ＝ １００ 的ＣＥ 算法來計算最優的ＦＲＦ 和Ｓ２ ＝ ５０ 的ＣＥ 算法計算最優的ＷＲＦ，就可以獲取比ＡＣＥ２ 算法更高的系統性能。這說明ＳＶＤ＿ＣＥ 方案有效降低了該目標問題的求解復雜度。由于采用ＩＳ 架構，對比最優的ＦＤ預編碼方案和全連接的ＯＭＰ 預編碼方案可以得到，ＩＳ 的系統結構還是會造成一定的系統性能損失。

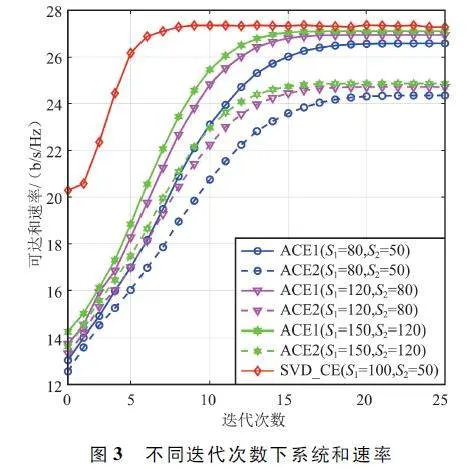
圖３ 展示了ＳＮＲ ＝ １０ ｄＢ、Ｎｔ ＝ １４４、Ｎｒ ＝ ４，Ｋ ＝ＮＲＦ ＝ Ｎｓ ＝ ４ 時，３ 種方案在不同迭代次數和不同候選數量集的情況下系統可達和速率的仿真結果。從圖中可以看出，隨著候選集Ｓ１ 和Ｓ２ 的增大，ＡＣＥ１和ＡＣＥ２ 方案得到的系統和速率相對更好，并且相對更快地收斂到最佳狀態。本文所采用的ＳＶＤ＿ＣＥ算法，在候選集的數量相對較小的情況下，迭代６ 次時就已收斂到最優值，所以本文提出的算法的復雜度明顯降低。

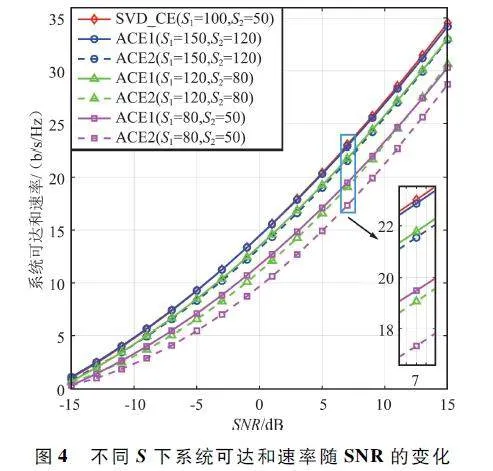
圖４ 展示了Ｎｔ ＝ １４４、Ｎｒ ＝ ４、Ｎｓ ＝ ＮＲＦ ＝ Ｋ ＝ ４ 的條件下，隨著ＳＮＲ 的變化，在總的迭代為１５ 次的前提下分別計算了在不同Ｓ１ 、Ｓ２ 的情況下采用ＡＣＥ 算法，以及采用ＳＶＤ＿ＣＥ 方案可以達到的系統和速率。從圖中可以看出，隨著Ｓ１ 、Ｓ２ 的增大，ＡＣＥ 的２ 種方案，系統和速率都在增大，而當Ｓ１ ＝ １５０、Ｓ２ ＝ １２０ 時，所采用的動態部分連接的ＡＣＥ 方案才達到與本文提出的ＳＶＤ＿ＣＥ 方案基本相同的系統和速率，這表明本文所提出的ＳＶＤ＿ＣＥ 方案相比ＡＣＥ 方案在降低求解復雜度的同時并不會造成明顯的系統性能損失。

３． ２ 系統能效分析

圖２ ～ 圖４ 的仿真結果已經證明，本文所采用的動態部分連接方案相比已有的ＡＣＥ２ 方案可以獲取更高的系統可達速率，為了衡量這種方案所帶來系統功耗損失，采用系統能效來分析３ 種預編碼的性能。系統能效定義為η ＝ Ｒ ／ Ｐｔｏｔａｌ，Ｒ 為系統可達速率，Ｐｔｏｔａｌ 為系統總功耗［２０］。對于ＦＤ 預編碼、動態部分連接ＳＶＤ＿ＣＥ、固定部分連接ＡＣＥ２ 和基于ＰＳ的ＯＭＰ 混合預編碼，根據４ 種不同的系統架構中所采用的硬件數量，其系統功耗可以分別表示為：

ＰＦＤ ＝ Ｐ ＋ Ｎｔ × ＰＲＦ ＋ ＰＦＢＢ ， （２０）

ＰＦＰＣ ＝ Ｐ ＋ ＮＲＦ × ＰＲＦ ＋ ＰＦＢＢ ＋ Ｎｔ × （Ｐｓｗ ＋ Ｐｉｎ ）， （２１）

ＰＳＰＣ ＝ Ｐ ＋ ＮＲＦ × ＰＲＦ ＋ ＰＦＢＢ ＋ Ｎｔ × （Ｐｓｗ ＋ Ｐｉｎ ）＋ … ＋（ＮＲＦ ＋ Ｎｔ）× Ｐｓｗ ， （２２）

Ｐｐｓ ＝ Ｐ ＋ ＮＲＦ × ＰＲＦ ＋ Ｎｔ × ＮＲＦ × Ｐｐｓ ， （２３）

式中：Ｐ 為系統信號傳輸功率，ＰＲＦ 為每條ＲＦ 的功耗，ＰＦＢＢ 為數字預編碼器的功耗，Ｐｓｗ 為開關器的功耗，Ｐｉｎ 為反相器的功耗。對于采用動態部分連接的預編碼，如圖１ 所示，加入了一個天線選擇器，假設這個器件的功耗近似等于（ＮＲＦ ＋Ｎｔ ）×Ｐｓｗ 。參考文獻［１４］的器件功耗配置方案，Ｐ ＝ ０． ０５ Ｗ，ＰＲＦ ＝０． ３ Ｗ，Ｐｓｗ ＝Ｐｉｎ ＝０． ００５ Ｗ，ＰＦＢＢ ＝ ０． ２ Ｗ，Ｐｐｓ ＝ ０． ０４ Ｗ。下面通過分析不同的ＲＦ 鏈路數（本文中假設ＲＦ 鏈路數等于傳輸數據流數）對系統能效的影響。

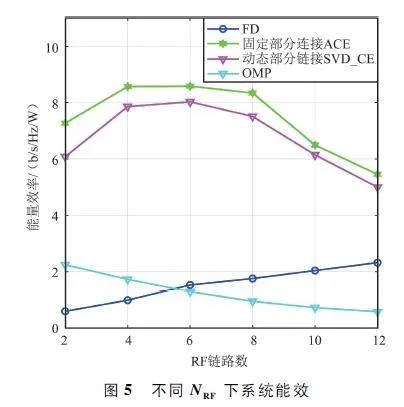
圖５ 展示了在ＳＮＲ ＝ １０ ｄＢ、Ｎｔ ＝ １２０、Ｎｒ ＝ ４、Ｋ ＝４ 時，不同ＮＲＦ 下系統能效。采用動態選擇的方案，增加了系統采用的硬件數量，所以其能量效率略小于采用固定部分連接方案。采用ＩＳ 架構的混合預編碼相比ＦＤ 的預編碼架構和基于ＰＳ 的ＯＭＰ 預編碼架構，其系統能效大大增加。隨著ＲＦ 數量的增加，ＩＳ 架構的預編碼ＲＦ 鏈路的功耗也在不斷增加，當ＲＦ 鏈路ＮＲＦ≥６ 時，由于分配給每個ＲＦ 鏈路的天線數在減少，導致系統可達速率降低，ＲＦ 鏈路增加導致系統功耗增大，所以其系統能效在逐漸下降。隨著ＲＦ 鏈數的增加，由于信道存在一定隨機性，直接固定每條ＲＦ 鏈路連接的天線將逐漸不如根據信道質量選擇最合適的天線所獲得系統可達速率，所以會導致固定部分連接的系統能效逐漸低于動態連接方案。

４ 結束語

考慮傳統預編碼系統會帶來較大功耗的問題，采用可以降低系統功耗的ＩＳ 預編碼架構，并研究了多用戶場景下混合預編碼的求解問題。針對ＩＳ 架構中求解混合預編碼矩陣而帶來大復雜度組合優化問題，放棄直接采用傳統復雜的深度學習方案進行求解，充分利用混合預編碼矩陣與最優的純數字預編碼矩陣之間存在的關聯性，提出動態分配的ＳＶＤ＿ＣＥ 方案進行求解。仿真結果充分表明，對比已有的ＡＣＥ 算法，所提算法不會造成系統性能的損失，但會大幅度降低離散組合優化的復雜度，而利用動態分配可進一步提升系統性能。考慮進一步提高低功耗結構下的系統性能指標，可以繼續研究自適應的動態連接結構和算法，以充分發揮大規模ＭＩＭＯ 系統的高增益性能。

參考文獻

［１］ 蔣建峰，孫金霞，尤瀾濤，等． 基于Ｍａｓｓｉｖｅ ＭＩＭＯ 及頻譜疊加的５Ｇ ＳＡ 網絡上行優化方法［Ｊ］． 無線電工程，２０２２，５２（１）：１２７－１３３．

［２］ 陶凱，孫哲． 一種用戶級多波束衛星系統預編碼算法［Ｊ］． 無線電工程，２０２０，５０（７）：５４９－５５３．

［３］ ＡＬＫＨＡＴＥＥＢ Ａ，ＭＯ Ｊ Ｈ，ＧＯＮＺＡＬＥＺＰＲＥＬＣＩＣ Ｎ，ｅｔ ａｌ．ＭＩＭＯ Ｐｒｅｃｏｄｉｎｇ ａｎｄ Ｃｏｍｂｉｎｉｎｇ Ｓｏｌｕｔｉｏｎｓ ｆｏｒ ｍｉｌｌｉｍｅｔｅｒＷａｖｅ Ｓｙｓｔｅｍｓ ［Ｊ ］． ＩＥＥＥ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｍａｇａｚｉｎｅ，２０１４，５２（１２）：１２２－１３１．

［４］ ＢＵＳＡＲＩ Ｓ Ａ，ＨＵＱ Ｋ Ｍ Ｓ，ＭＵＭＴＡＺ Ｓ，ｅｔ ａｌ． Ｍｉｌｌｉｍｅｔｅｒｗａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ Ｃｏｍｍｕｎｉｃａｔｉｏｎ ｆｏｒ Ｆｕｔｕｒｅ ＷｉｒｅｌｅｓｓＳｙｓｔｅｍｓ：Ａ Ｓｕｒｖｅｙ ［Ｊ］． ＩＥＥＥ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｓｕｒｖｅｙｓａｎｄ Ｔｕｔｏｒｉａｌｓ，２０１８，２０（２）：８３６－８６９．

［５］ ＪＩＮ Ｊ Ｎ，ＺＨＥＮＧ Ｙ Ｒ，ＣＨＥＮ Ｗ，ｅｔ ａｌ． Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇｆｏｒ Ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ： Ａ ＭａｔｒｉｘＦａｃｔｏｒｉｚａｔｉｏｎ Ａｐｐｒｏａｃｈ ［Ｊ ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎＷｉｒｅｌｅｓｓ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０１８，１７（５）：３３２７－３３３９．

［６］ ＹＵ Ｘ Ｈ，ＳＨＥＮ Ｊ Ｃ，ＺＨＡＮＧ Ｊ，ｅｔ ａｌ． Ａｌｔｅｒｎａｔｉｎｇ Ｍｉｎｉｍｉｚａｔｉｏｎ Ａｌｇｏｒｉｔｈｍｓ ｆｏｒ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｉｎ ＭｉｌｌｉｍｅｔｅｒＷａｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ ［Ｊ ］． ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｆ ＳｅｌｅｃｔｅｄＴｏｐｉｃｓ ｉｎ Ｓｉｇｎａｌ Ｐｒｏｃｅｓｓｉｎｇ，２０１６，１０（３）：４８５－５００．

［７］ ＷＡＮＧ Ｓ Ｇ，ＬＩ Ｚ Ｔ，ＨＥ Ｍ Ｙ，ｅｔ ａｌ． Ａ Ｊｏｉｎｔ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ／ Ｃｏｍｂｉｎｉｎｇ Ｓｃｈｅｍｅ Ｂａｓｅｄ ｏｎ Ｅｑｕｉｖａｌｅｎｔ Ｃｈａｎｎｅｌｆｏｒ Ｍａｓｓｉｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ［Ｊ］． ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｎ ＳｅｌｅｃｔｅｄＡｒｅａｓ ｉｎ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０２２，４０（１０）：２８８２－２８９３．

［８］ ＲＯＨＡＴＧＩ Ａ，ＲＡＷＡＴ Ｍ． Ｍｏｄｉｆｉｅｄ Ｌｏｗ Ｃｏｍｐｌｅｘｉｔｙ Ｐｒｅｃｏｄｉｎｇ Ａｌｇｏｒｉｔｈｍ ｆｏｒ Ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ［Ｃ］∥２０１８ Ｓｅｃｏｎｄ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｃｏｍｐｕｔｉｎｇ ａｎｄ Ｃｏｎｔｒｏｌ Ｓｙｓｔｅｍｓ （ＩＣＩＣＣＳ）． Ｍａｄｕｒａｉ：ＩＥＥＥ，２０１８：１０６６－１０６９．

［９］ ＩＯＵＳＨＵＡ Ｓ Ｓ，ＥＬＤＡＲ Ｙ Ｃ． Ａ Ｆａｍｉｌｙ ｏｆ Ｈｙｂｒｉｄ ＡｎａｌｏｇＤｉｇｉｔａｌ Ｂｅａｍｆｏｒｍｉｎｇ Ｍｅｔｈｏｄｓ ｆｏｒ Ｍａｓｓｉｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｓｉｇｎａｌ Ｐｒｏｃｅｓｓｉｎｇ，２０１９，６７（１２）：３２４３－３２５７．

［１０］ ＹＵ Ｓ Ｊ，ＧＵＯ Ｎ，ＬＩ Ｗ Ｔ，ｅｔ ａｌ． Ｌｏｗｐｏｗｅｒ ＣｏｎｓｕｍｐｔｉｏｎＨｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｆｏｒ Ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ［Ｃ］∥２０２０ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｃｏｍｐｕｔｉｎｇ，Ｎｅｔｗｏｒｋｉｎｇ ａｎｄ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ （ＩＣＮＣ）． Ｂｉｇ Ｉｓｌａｎｄ：ＩＥＥＥ，２０２０：１０３８－１０４１．

［１１］ ＬＩＵ Ｆ Ｌ，ＢＡＩ Ｘ Ｙ，ＳＨＩ Ｈ Ｙ，ｅｔ ａｌ． Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｗｉｔｈＡｄａｐｔｉｖｅ Ｓｕｂｃｏｎｎｅｃｔｅｄ Ａｒｃｈｉｔｅｃｔｕｒｅ ｆｏｒ ｍｍＷａｖｅＭａｓｓｉｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ［Ｃ］∥２０２０ ＩＥＥＥ ３１ｓｔ Ａｎｎｕａｌ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｓｙｍｐｏｓｉｕｍ ｏｎ Ｐｅｒｓｏｎａｌ，Ｉｎｄｏｏｒ ａｎｄ ＭｏｂｉｌｅＲａｄｉｏ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ． Ｌｏｎｄｏｎ：ＩＥＥＥ，２０２０：１－６．

［１２］ ＬＩＡＯ Ｇ Ｙ，ＺＨＡＯ Ｆ． Ｄｙｎａｍｉｃａｌｌｙ ＳｕｂａｒｒａｙｃｏｎｎｅｃｔｅｄＨｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ Ｓｃｈｅｍｅ ｆｏｒ Ｍｕｌｔｉｕｓｅｒ ｍｉｌｌｉｍｅｔｅｒＷａｖｅＭａｓｓｉｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ ［Ｊ ］． Ｗｉｒｅｌｅｓｓ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓａｎｄ Ｍｏｂｉｌｅ Ｃｏｍｐｕｔｉｎｇ，２０２１，２０２１：１－１０．

［１３］ ＸＵＥ Ｘ，ＷＡＮＧ Ｙ Ｃ，ＹＡＮＧ Ｌ，ｅｔ ａｌ． Ｅｎｅｒｇｙｅｆｆｉｃｉｅｎｔ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｆｏｒ Ｍａｓｓｉｖｅ ＭＩＭＯ ｍｍＷａｖｅ Ｓｙｓｔｅｍｓ ｗｉｔｈａ Ｆｕｌｌｙａｄａｐｔｉｖｅｃｏｎｎｅｃｔｅｄ Ｓｔｒｕｃｔｕｒｅ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓｏｎ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０２０，６８（６）：３５２１－３５３５．

［１４］ ＧＡＯ Ｘ Ｙ，ＤＡＩ Ｌ Ｌ，ＳＵＮ Ｙ，ｅｔ ａｌ． Ｍａｃｈｉｎｅ Ｌｅａｒｎｉｎｇ Ｉｎｓｐｉｒｅｄ Ｅｎｅｒｇｙｅｆｆｉｃｉｅｎｔ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｆｏｒ ｍｍＷａｖｅＭａｓｓｉｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ ［Ｃ］∥ ２０１７ ＩＥＥＥ ＩｎｔｅｒｎａｔｉｏｎａｌＣｏｎｆｅｒｅｎｃｅ ｏｎ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ （ＩＣＣ ）． Ｐａｒｉｓ：ＩＥＥＥ，２０１７：１－６．

［１５］ ＨＵ Ｃ Ｃ，ＬＩＮ Ｗ Ｃ，ＬＥＥ Ｃ Ｊ． Ｇｅｎｅｒａｌｉｚｅｄ Ｓｐａｔｉａｌ Ｍｏｄｕｌａｔｉｏｎ Ａｉｄｅｄ ｍｍＷａｖｅ Ｍａｓｓｉｖｅ ＭＩＭＯ Ｓｙｓｔｅｍｓ ｗｉｔｈ ＳｗｉｔｃｈａｎｄＩｎｖｅｒｔｅｒ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ Ｄｅｓｉｇｎ［Ｊ］． ＩＥＥＥ ＳｙｓｔｅｍｓＪｏｕｒｎａｌ，２０２２，１７（１）：５３６－５４５．

［１６］ ＡＬＫＨＡＴＥＥＢ Ａ，ＬＥＵＳ Ｇ，ＨＥＡＴＨ Ｒ Ｗ． ＬｉｍｉｔｅｄＦｅｅｄｂａｃｋ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｆｏｒ Ｍｕｌｔｉｕｓｅｒ ＭｉｌｌｉｍｅｔｅｒＷａｖｅ Ｓｙｓｔｅｍｓ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｗｉｒｅｌｅｓｓ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０１５，１４（１１）：６４８１－６４９４．

［１７］ ＴＩＡＮ Ｘ Ｗ，ＬＩＵ Ｑ，ＷＡＮＧ Ｚ Ｈ，ｅｔ ａｌ． Ｓｅｃｕｒｅ ＨｙｂｒｉｄＢｅａｍｆｏｒｍｅｒｓ Ｄｅｓｉｇｎ ｉｎ ｍｍＷａｖｅ ＭＩＭＯ Ｗｉｒｅｔａｐ Ｓｙｓｔｅｍｓ［Ｊ］． ＩＥＥＥ Ｓｙｓｔｅｍｓ Ｊｏｕｒｎａｌ，２０２０，１４（１）：５４８－５５９．

［１８］ ＺＨＡＮＧ Ｄ，ＰＡＮ Ｐ，ＹＯＵ Ｒ Ｎ，ｅｔ ａｌ． ＳＶＤｂａｓｅｄ Ｌｏｗｃｏｍｐｌｅｘｉｔｙ Ｈｙｂｒｉｄ Ｐｒｅｃｏｄｉｎｇ ｆｏｒ ｍｉｌｌｉｍｅｔｅｒＷａｖｅ ＭＩＭＯＳｙｓｔｅｍｓ ［Ｊ ］． ＩＥＥＥ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ Ｌｅｔｔｅｒｓ，２０１８，２２（１０）：２１７６－２１７９．

［１９］ ＡＹＡＣＨ Ｏ Ｅ，ＲＡＪＡＧＯＰＡＬ Ｓ，ＡＢＵＳＵＲＲＡ Ｓ，ｅｔ ａｌ． Ｓｐａｔｉａｌｌｙ Ｓｐａｒｓｅ Ｐｒｅｃｏｄｉｎｇ ｉｎ Ｍｉｌｌｉｍｅｔｅｒ Ｗａｖｅ ＭＩＭＯＳｙｓｔｅｍｓ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｗｉｒｅｌｅｓｓ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０１４，１３（３）：１４９９－１５１３．

［２０］ ＧＡＯ Ｘ Ｙ，ＤＡＩ Ｌ Ｌ，ＨＡＮ Ｓ Ｆ，ｅｔ ａｌ． Ｅｎｅｒｇｙｅｆｆｉｃｉｅｎｔ Ｈｙｂｒｉｄ Ａｎａｌｏｇ ａｎｄ Ｄｉｇｉｔａｌ Ｐｒｅｃｏｄｉｎｇ ｆｏｒ ｍｍＷａｖｅ ＭＩＭＯＳｙｓｔｅｍｓ ｗｉｔｈ Ｌａｒｇｅ Ａｎｔｅｎｎａ Ａｒｒａｙｓ［Ｊ］． ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｎＳｅｌｅｃｔｅｄ Ａｒｅａｓ ｉｎ Ｃｏｍｍｕｎｉｃａｔｉｏｎｓ，２０１６，３４ （４ ）：９９８－１００９．

作者簡介

王華華 男，（１９８１—），碩士，正高級工程師。主要研究方向：移動通信基帶信號處理、移動通信空口安全。

（*通信作者）曹 磊 男，（１９９９—），碩士研究生。主要研究方向：移動通信物理層算法、毫米波混合預編碼。

羅一丹 男，（１９９８—），碩士研究生。主要研究方向：移動通信物理層算法和波束賦形技術。

基金項目：重慶市自然科學基金（ｃｓｔｃ２０２１ｊｃｙｉ-ｍｓｘｍＸ０４５４）