幾何畫板巧助

[摘 要] 依托幾何畫板軟件，借鑒理化學(xué)科實(shí)驗(yàn)，進(jìn)行數(shù)學(xué)創(chuàng)新實(shí)驗(yàn)，學(xué)生自主操作探究，思索現(xiàn)象背后原因，深刻認(rèn)識(shí)問題本質(zhì)，提升數(shù)學(xué)核心素養(yǎng).

[關(guān)鍵詞] 幾何畫板;創(chuàng)新實(shí)驗(yàn);自主操作;核心素養(yǎng)

《加快推進(jìn)教育現(xiàn)代化實(shí)施方案（2018—2022年）》指出：“促進(jìn)信息技術(shù)與教育教學(xué)深度融合，支持學(xué)校充分利用信息技術(shù)開展人才培養(yǎng)模式和教學(xué)方法改革，逐步實(shí)現(xiàn)信息化教與學(xué)應(yīng)用師生全覆蓋. ”教育信息化是當(dāng)前教育發(fā)展的必然趨勢(shì). 以信息技術(shù)軟件為載體，進(jìn)行數(shù)學(xué)創(chuàng)新實(shí)驗(yàn)，營(yíng)造數(shù)學(xué)實(shí)驗(yàn)教學(xué)新常態(tài)，應(yīng)成為教育信息化的關(guān)鍵舉措. 下面筆者以“圓周角定理的探究與證明”為例，展示幾何畫板支持下的數(shù)學(xué)創(chuàng)新實(shí)驗(yàn)如何開展，并結(jié)合本實(shí)驗(yàn)芻談對(duì)創(chuàng)新實(shí)驗(yàn)教學(xué)的思考.

實(shí)驗(yàn)?zāi)康?/p>

（1）借助幾何畫板畫同弧所對(duì)的圓周角，發(fā)現(xiàn)圓周角的度數(shù)與它所對(duì)弧上的圓心角度數(shù)的關(guān)系、同弧或等弧所對(duì)的圓周角的關(guān)系，猜想出圓周角定理.

（2）通過從特殊到一般、再?gòu)囊话愕教厥獾姆椒ǎC明圓周角定理，體會(huì)圓周角定理證明方法的獨(dú)特性，感受分類討論、轉(zhuǎn)化等數(shù)學(xué)思想.

（3）激發(fā)問題探究意識(shí)，發(fā)展數(shù)學(xué)推理能力，學(xué)會(huì)用數(shù)學(xué)的眼光觀察、用數(shù)學(xué)的思維思考以及用數(shù)學(xué)的語(yǔ)言表達(dá)，發(fā)展數(shù)學(xué)核心素養(yǎng).

實(shí)驗(yàn)準(zhǔn)備

（1）實(shí)驗(yàn)器材. 本實(shí)驗(yàn)所用器材是臺(tái)式電腦（可在電腦教室，要求每生一臺(tái)）和幾何畫板軟件.

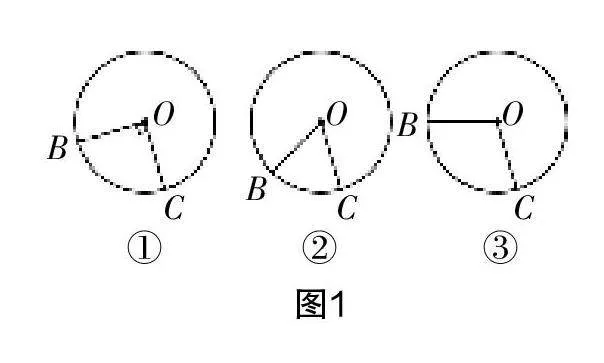
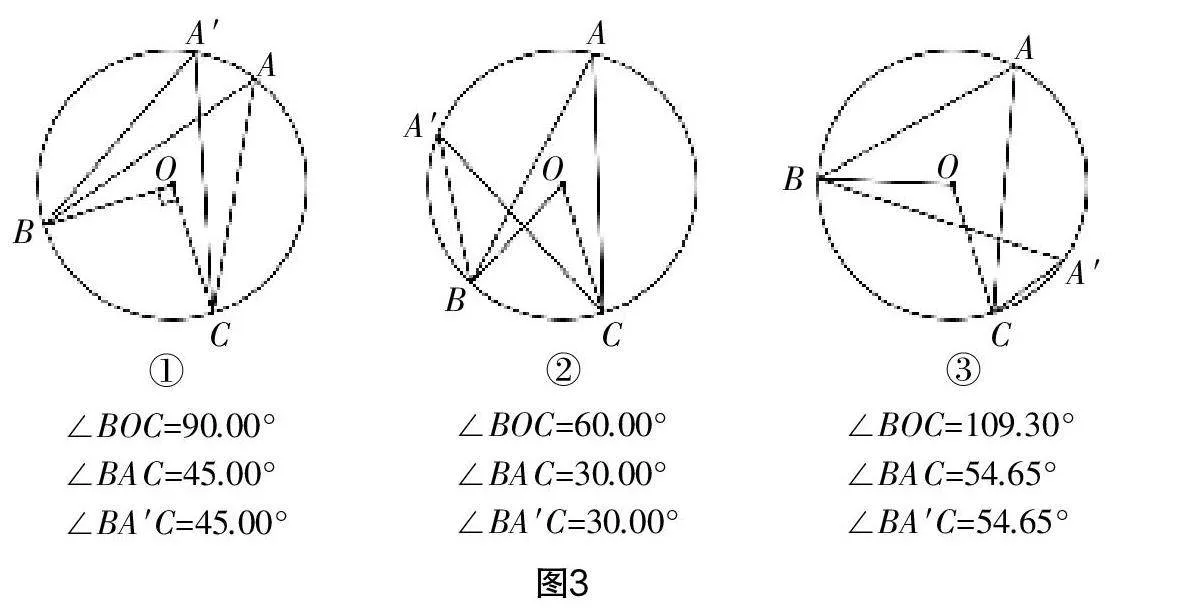
（2）實(shí)驗(yàn)素材. 為確保實(shí)驗(yàn)探究的高效性，保障實(shí)驗(yàn)素材的一致性，教師提前利用幾何畫板軟件制作了3種不同情況下的圖形（如圖1，B，C是☉O上的兩點(diǎn)，連OB，OC）：①∠BOC=90°;②∠BOC=60°;③任意∠BOC. 3種圖形中點(diǎn)B和點(diǎn)C在保證數(shù)學(xué)關(guān)系不變的前提下可在☉O上自由運(yùn)動(dòng)，既能夠確保弧所在位置的任意性，又便于驗(yàn)證等弧所對(duì)圓周角的性質(zhì).

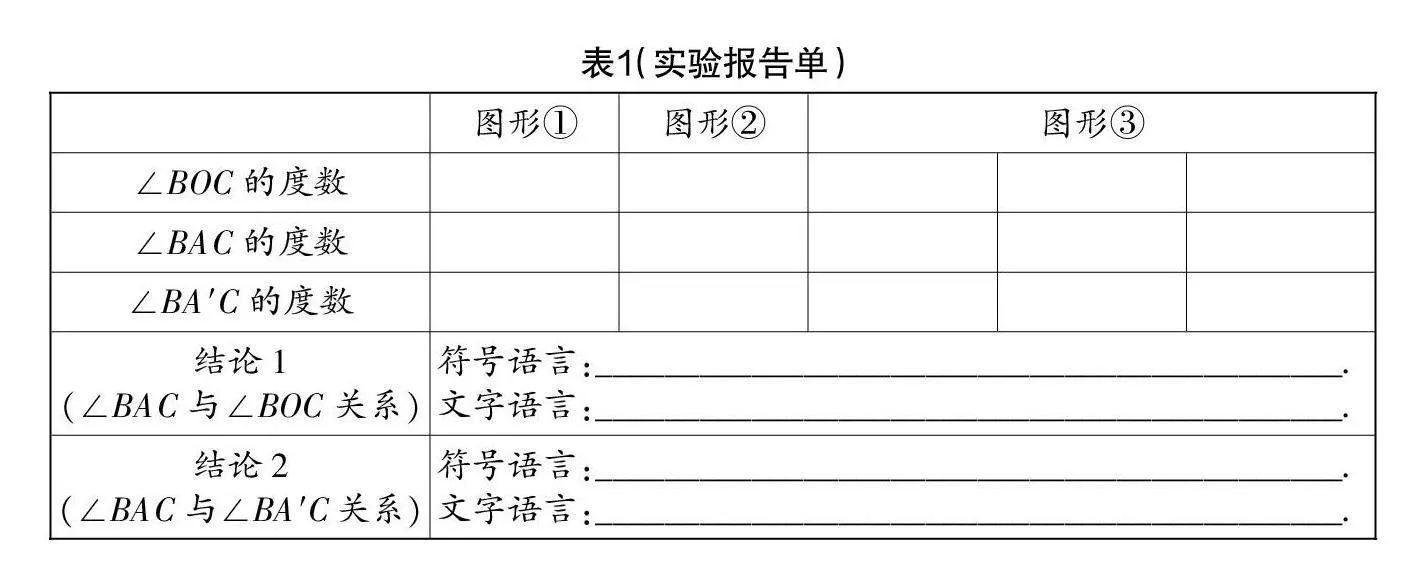
（3）實(shí)驗(yàn)報(bào)告單. 類比物理、化學(xué)實(shí)驗(yàn)報(bào)告單，教師設(shè)計(jì)了本實(shí)驗(yàn)對(duì)應(yīng)的報(bào)告單，具體如表1（記所對(duì)的一個(gè)圓周角為∠BAC，另一個(gè)圓周角為∠BA′C）.

實(shí)驗(yàn)教學(xué)

1. 提出問題

教師介紹圓周角的概念：頂點(diǎn)在圓上，并且兩邊都和圓相交的角叫圓周角. 待學(xué)生理解圓周角的概念并能準(zhǔn)確識(shí)別圓周角后，教師提出問題：圓周角的度數(shù)與它所對(duì)弧上的圓心角度數(shù)有什么關(guān)系？同弧或等弧所對(duì)的圓周角有什么關(guān)系？

2. 實(shí)驗(yàn)探究

教師打開幾何畫板軟件，就本實(shí)驗(yàn)中幾何畫板的操作步驟進(jìn)行演示，使學(xué)生掌握幾何畫板的基本操作，學(xué)會(huì)幾何畫板的角度度量功能. 學(xué)生一邊觀察教師演示，一邊進(jìn)行畫板操作，迅速掌握操作步驟. 接著，教師把提前制作好的3種圖形分享給學(xué)生，同時(shí)巡視指導(dǎo)學(xué)生開展實(shí)驗(yàn). 學(xué)生自主進(jìn)行實(shí)驗(yàn)，必要時(shí)進(jìn)行小組合作，順利完成實(shí)驗(yàn)操作，填寫實(shí)驗(yàn)報(bào)告單（表1）.

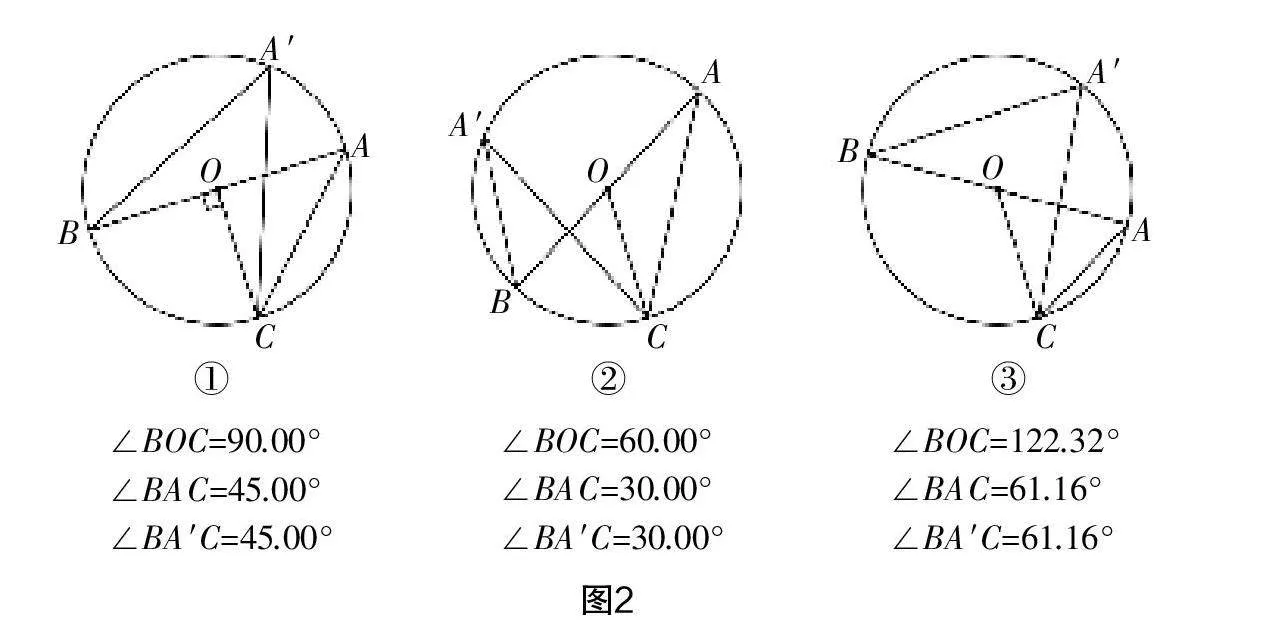
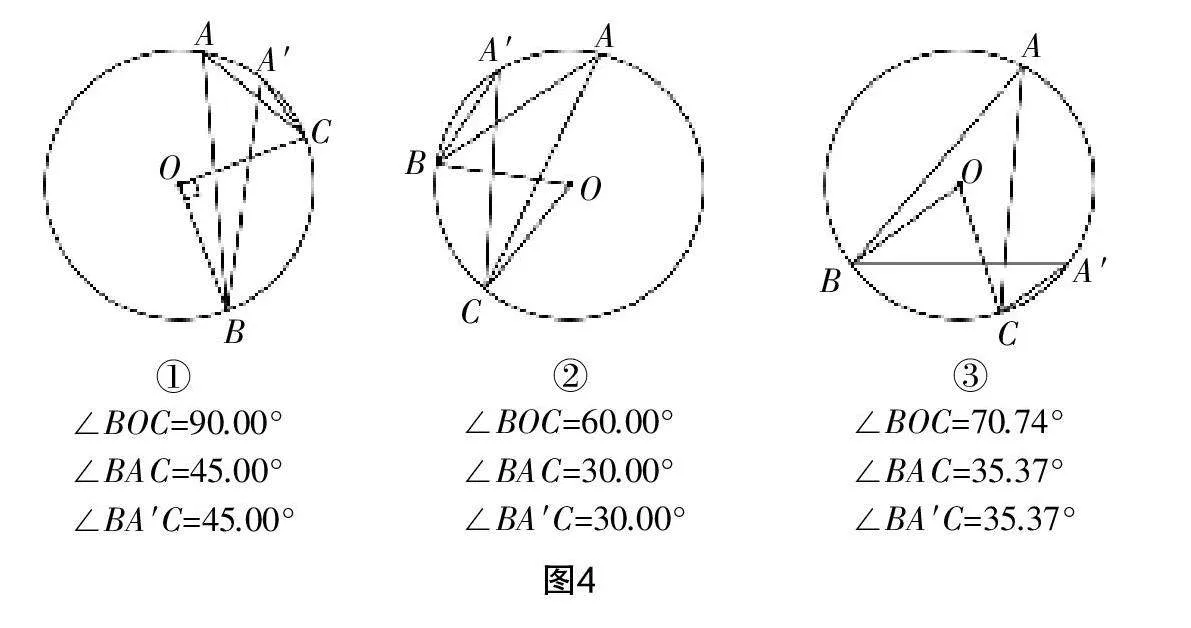
學(xué)生借助幾何畫板中的角度度量功能分別度量出∠BOC，∠BAC和∠BA′C的度數(shù). 教師隨機(jī)呈現(xiàn)3位學(xué)生實(shí)驗(yàn)過程中的操作界面，由于樣本呈現(xiàn)的隨機(jī)性，所以選取的樣本具有代表性，能夠反映全體學(xué)生的實(shí)驗(yàn)情況. 通過操作界面的對(duì)比，發(fā)現(xiàn)3個(gè)圖形都既有特殊形態(tài)又有一般形態(tài)，呈現(xiàn)出來的都既有靜態(tài)數(shù)據(jù)又有動(dòng)態(tài)數(shù)據(jù)，具體如圖2、圖3和圖4.

學(xué)生結(jié)合自己的實(shí)驗(yàn)操作，完成實(shí)驗(yàn)報(bào)告單的填寫，得出如下兩個(gè)結(jié)論：（1）圓周角的度數(shù)等于它所對(duì)弧上的圓心角度數(shù)的一半;（2）同弧或等弧所對(duì)的圓周角相等.

3. 分析證明

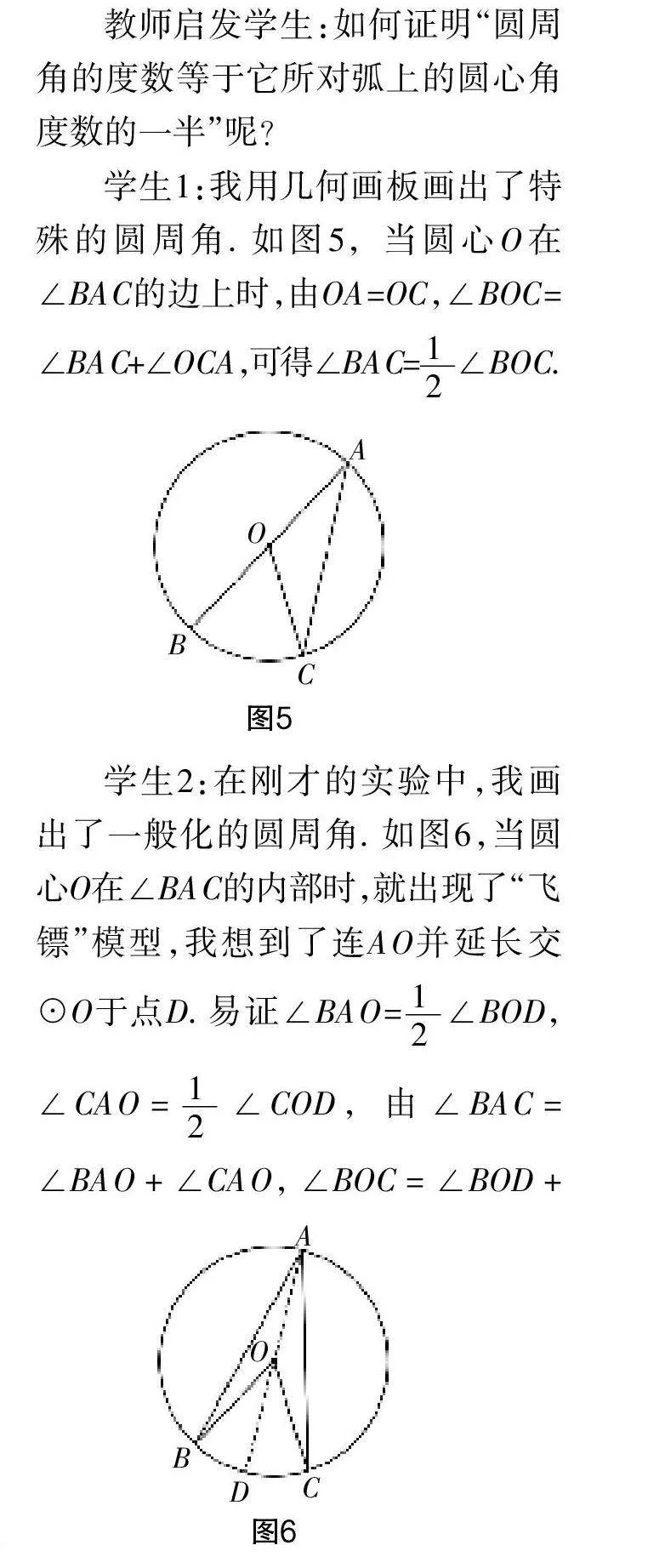
教師啟發(fā)學(xué)生：如何證明“圓周角的度數(shù)等于它所對(duì)弧上的圓心角度數(shù)的一半”呢？

學(xué)生1：我用幾何畫板畫出了特殊的圓周角. 如圖5，當(dāng)圓心O在∠BAC的邊上時(shí)，由OA=OC，∠BOC=∠BAC+∠OCA，可得∠BAC=∠BOC.

學(xué)生2：在剛才的實(shí)驗(yàn)中，我畫出了一般化的圓周角. 如圖6，當(dāng)圓心O在∠BAC的內(nèi)部時(shí)，就出現(xiàn)了“飛鏢”模型，我想到了連AO并延長(zhǎng)交☉O于點(diǎn)D. 易證∠BAO=∠BOD，∠CAO=∠COD，由∠BAC=∠BAO+∠CAO，∠BOC=∠BOD+∠COD，得出∠BAC=∠BOC.

學(xué)生3：在圖6（輔助線已作）的基礎(chǔ)上，我拖動(dòng)點(diǎn)A使圓心O在∠BAC的外部. 如圖7，易證∠BAO=∠BOD，∠CAO=∠COD，因?yàn)椤螧AC=∠BAO-∠CAO，∠BOC=∠BOD-∠COD，所以∠BAC=∠BOC.

學(xué)生4：我拖動(dòng)點(diǎn)A使圓心O在∠BAC的外部. 如圖8，易證∠BAO=∠BOD，∠CAO=∠COD，由∠BAC=∠CAO-∠BAO，∠BOC=∠COD-∠BOD，得出∠BAC=∠BOC.

教師追問：如何證明“同弧或等弧所對(duì)的圓周角相等”呢？

學(xué)生能夠根據(jù)“同弧或等弧所對(duì)的圓心角相等”，得出“同弧或等弧所對(duì)的圓周角相等”.

教師告知學(xué)生先前探究和證明的兩個(gè)結(jié)論就是圓周角定理的內(nèi)容，并把圓周角定理板書在黑板上，然后畫出相應(yīng)圖形，結(jié)合學(xué)生的回答形成該定理符號(hào)語(yǔ)言表述的板書.

4. 檢驗(yàn)收獲

教師設(shè)置開放性問題如下：如圖9，A，B，C，D，E，F(xiàn)是☉O上的點(diǎn)，=，∠BAC=35°，你能求出哪些角的度數(shù)？請(qǐng)說明理由.

學(xué)生積極分享想法，求出∠BOC，∠BFC和∠CED的度數(shù)，并利用圓周角定理說明理由.

最后，教師指導(dǎo)學(xué)生就本實(shí)驗(yàn)進(jìn)行反思與交流，引導(dǎo)學(xué)生描述感受、表達(dá)收獲、總結(jié)發(fā)現(xiàn).

實(shí)驗(yàn)反思

1. 運(yùn)用信息技術(shù)手段，開發(fā)創(chuàng)新實(shí)驗(yàn)素材

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》指出：“利用數(shù)學(xué)專用軟件等教學(xué)工具開展數(shù)學(xué)實(shí)驗(yàn)，將抽象的數(shù)學(xué)知識(shí)直觀化，促進(jìn)學(xué)生對(duì)數(shù)學(xué)概念的理解和數(shù)學(xué)知識(shí)的建構(gòu). ”借助幾何畫板等軟件，開發(fā)創(chuàng)新實(shí)驗(yàn)素材，是開展創(chuàng)新實(shí)驗(yàn)的重要手段. 本實(shí)驗(yàn)中，教師利用幾何畫板軟件制作了3種圖形，為學(xué)生直接開展實(shí)驗(yàn)搭建了平臺(tái)，學(xué)生不參與復(fù)雜素材的開發(fā)過程，只參與利用素材探究問題的實(shí)驗(yàn)過程，這就使得數(shù)學(xué)實(shí)驗(yàn)得以高效開展.

2. 借鑒理化實(shí)驗(yàn)過程，豐富實(shí)驗(yàn)探究?jī)?nèi)涵

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》指出：“設(shè)立跨學(xué)科主題學(xué)習(xí)活動(dòng)，加強(qiáng)學(xué)科間相互關(guān)聯(lián)，帶動(dòng)課程綜合化實(shí)施，強(qiáng)化實(shí)踐性要求. ”理化學(xué)科實(shí)驗(yàn)內(nèi)容較多，而且相對(duì)比較成熟，而數(shù)學(xué)實(shí)驗(yàn)還處在探索階段，有必要借鑒學(xué)科關(guān)聯(lián)度較高的理化實(shí)驗(yàn). 本實(shí)驗(yàn)中，教師為每位學(xué)生配備了實(shí)驗(yàn)器材、實(shí)驗(yàn)素材和實(shí)驗(yàn)報(bào)告單，使數(shù)學(xué)實(shí)驗(yàn)具備了較成熟的硬性條件，這樣的實(shí)驗(yàn)探究是有豐富內(nèi)涵的真探究，達(dá)到了預(yù)期的實(shí)驗(yàn)?zāi)康?

3. 強(qiáng)調(diào)學(xué)生切身體驗(yàn)，發(fā)展數(shù)學(xué)核心素養(yǎng)

數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)的積累是提高學(xué)生數(shù)學(xué)素養(yǎng)的重要標(biāo)志，數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)需要在“做”的過程和思考的過程中積淀，是在數(shù)學(xué)學(xué)習(xí)活動(dòng)過程中逐步積累的. 眼睛能觀察到的數(shù)學(xué)、動(dòng)手能操作到的數(shù)學(xué)和用心能感受到的數(shù)學(xué)，是學(xué)生能切身體驗(yàn)到的數(shù)學(xué)，這樣的數(shù)學(xué)學(xué)習(xí)是最具成效的. 本實(shí)驗(yàn)中，學(xué)生親身參與“做”數(shù)學(xué)實(shí)驗(yàn)，發(fā)現(xiàn)了圓周角定理，在思考中證明了圓周角定理，認(rèn)識(shí)到實(shí)驗(yàn)現(xiàn)象背后的問題本質(zhì)，積累了數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)，發(fā)展了數(shù)學(xué)核心素養(yǎng).