APOS理論與變式教學(xué)理論深度融合的實(shí)踐與研究

［摘 要］ APOS理論與變式教學(xué)理論對(duì)概念教學(xué)均具有指導(dǎo)意義，如何將兩者有機(jī)地融合在一起，進(jìn)一步提升概念教學(xué)的成效呢？研究者以“函數(shù)的概念”教學(xué)為例，將APOS理論的四個(gè)階段作為教學(xué)主線，把變式有機(jī)地融合在各個(gè)階段中，形成相互促進(jìn)的教學(xué)策略.

［關(guān)鍵詞］ APOS理論；變式；概念

概念是數(shù)學(xué)的靈魂，在教學(xué)中占有重要地位. 近年來(lái)，對(duì)概念教學(xué)的研究方興未艾，尤其是各種新興教學(xué)手段的涌現(xiàn)，令不少教師眼花繚亂. 采取怎樣的教學(xué)手段實(shí)施概念教學(xué)可取得最佳的教學(xué)成效呢？事實(shí)證明，將APOS理論與變式教學(xué)理論深度融合，不僅能深刻揭露概念的內(nèi)涵與外延，還能發(fā)展學(xué)生的數(shù)學(xué)思維，提升學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng).

核心概念的界定

1. APOS理論

APOS理論是由美國(guó)數(shù)學(xué)教育學(xué)家杜賓斯基提出的，屬于建構(gòu)主義理論的一個(gè)分支，主要針對(duì)數(shù)學(xué)概念教學(xué)而言. APOS理論主張概念教學(xué)以學(xué)習(xí)者自主探究為主，學(xué)習(xí)者親歷發(fā)現(xiàn)、分析與思考概念的過(guò)程，形成深刻認(rèn)識(shí). APOS理論認(rèn)為，概念學(xué)習(xí)并不是被動(dòng)接受的過(guò)程，而是個(gè)體主觀能動(dòng)地經(jīng)歷活動(dòng)、過(guò)程、對(duì)象與圖式四個(gè)階段. 這四個(gè)階段并非獨(dú)立存在的個(gè)體，而是逐層遞進(jìn)、相伴相依的群體.

第一階段：活動(dòng).

活動(dòng)的關(guān)鍵在于帶領(lǐng)學(xué)生初步認(rèn)識(shí)與了解研究對(duì)象，學(xué)生對(duì)外部不熟悉的信息進(jìn)行加工、轉(zhuǎn)化，形成自己能理解的內(nèi)容. 在此過(guò)程中，最常規(guī)的操作方法就是借助學(xué)生熟悉的生活材料創(chuàng)設(shè)情境，吸引學(xué)生積極主動(dòng)地參與教學(xué)活動(dòng)，教師在必要時(shí)給予適當(dāng)引導(dǎo)，幫助學(xué)生更好地感知概念原型與概念之間的聯(lián)系.

第二階段：過(guò)程.

過(guò)程階段是指學(xué)生對(duì)活動(dòng)過(guò)程的調(diào)整、思考，對(duì)知識(shí)達(dá)到熟練的程度，并在腦海中組建一套操作體系，經(jīng)歸納、總結(jié)、壓縮等處理，抽象出共同特征形成概念. 此為量變到質(zhì)變的過(guò)程. 在該階段中，學(xué)生無(wú)須接受活動(dòng)的刺激，就能憑借自己的大腦實(shí)施活動(dòng). 對(duì)學(xué)優(yōu)生而言，過(guò)程階段可將已有活動(dòng)與其他活動(dòng)相組合，將具體實(shí)操轉(zhuǎn)化為抽象思維，有效促進(jìn)邏輯思維能力的發(fā)展.

第三階段：對(duì)象.

對(duì)象階段在于獲得可以心理操作的對(duì)象，想要獲得這個(gè)對(duì)象，學(xué)生需要壓縮活動(dòng)與過(guò)程階段，將它們作為整體進(jìn)行應(yīng)用. 到對(duì)象階段時(shí)，學(xué)生腦海中就會(huì)對(duì)概念形成一種靜態(tài)的結(jié)構(gòu)關(guān)系，便于學(xué)生從整體的角度理解概念本質(zhì). 在此過(guò)程中，學(xué)生還能對(duì)概念賦予形式化的符號(hào)，并以此作為研究對(duì)象開(kāi)展活動(dòng).

第四階段：圖式.

此為APOS理論的最后環(huán)節(jié)，是新舊知識(shí)整合補(bǔ)充，構(gòu)建新圖式結(jié)構(gòu)的過(guò)程. 新圖式對(duì)某些（類）問(wèn)題納入其中會(huì)呈現(xiàn)出不同的反饋，學(xué)生親歷概念持續(xù)建構(gòu)的整個(gè)流程，形成高階思維與心理表征，此為發(fā)展數(shù)學(xué)學(xué)科核心素養(yǎng)的基礎(chǔ).

2. 變式教學(xué)理論

變式是指改變問(wèn)題的表征形式，變化問(wèn)題的非本質(zhì)屬性（本質(zhì)屬性不改變），學(xué)生從中獲得研究對(duì)象的本質(zhì)與規(guī)律的一種教學(xué)方法. 變式主要包含概念性變式與過(guò)程性變式兩類. 概念性變式所研究的對(duì)象一般是靜態(tài)、獨(dú)立的問(wèn)題；過(guò)程性變式關(guān)注的是數(shù)學(xué)學(xué)習(xí)對(duì)象動(dòng)態(tài)的、層次性遞進(jìn)的過(guò)程. 變式教學(xué)具備開(kāi)闊思維、靈活思維、深化思維等作用，還彰顯教學(xué)活動(dòng)的探究性，是促進(jìn)學(xué)生更好掌握概念的基本方法.

融合的意義

概念本身具有過(guò)程與對(duì)象二重性特征，它不僅是一種靜態(tài)的知識(shí)結(jié)構(gòu)，還是一個(gè)動(dòng)態(tài)的操作過(guò)程. 因此，在實(shí)施概念教學(xué)時(shí)，應(yīng)動(dòng)靜結(jié)合才能取得預(yù)期的效果. APOS理論與變式教學(xué)理論雖然都能增加概念教學(xué)實(shí)效，但在實(shí)際應(yīng)用時(shí)，鮮有教師將這兩個(gè)理論整合在一起實(shí)施教學(xué). 實(shí)踐發(fā)現(xiàn)，將這兩種理論深度融合在一起實(shí)施概念教學(xué)，可有效激發(fā)學(xué)生對(duì)概念的探索欲，揭露概念的內(nèi)涵與外延. 筆者以“函數(shù)的概念”教學(xué)為例，探討這兩種理論融合在一起的具體措施.

例談實(shí)施措施

函數(shù)是幾何與代數(shù)的結(jié)合，與學(xué)生的生活有著密切聯(lián)系. APOS理念與概念的形成過(guò)程具有一致性，將變式教學(xué)理論有機(jī)地融合到APOS理論的應(yīng)用中，可進(jìn)一步增強(qiáng)學(xué)生對(duì)概念的理解.

1. 活動(dòng)階段——初步建構(gòu)概念

活動(dòng)1 一輛高速列車加速到350 km/h后保持勻速運(yùn)行半小時(shí).

問(wèn)題1：這半小時(shí)之內(nèi)，列車行進(jìn)的路程S與運(yùn)行時(shí)間t之間存在什么關(guān)系？是不是函數(shù)關(guān)系？理由是什么？

問(wèn)題2：該列車運(yùn)行一小時(shí)就前進(jìn)了350 km，對(duì)嗎？

問(wèn)題3：請(qǐng)用規(guī)范的數(shù)學(xué)語(yǔ)言來(lái)描述路程S與時(shí)間t之間存在怎樣的對(duì)應(yīng)關(guān)系.

（學(xué)生獨(dú)立思考、合作交流，教師展示典型結(jié)論，并引導(dǎo)學(xué)生點(diǎn)評(píng). ）

設(shè)計(jì)意圖 該活動(dòng)主要突出列車行駛過(guò)程中時(shí)間與路程的關(guān)系，學(xué)生從“變量說(shuō)”的角度出發(fā)，可順利解決第一個(gè)問(wèn)題；第二個(gè)問(wèn)題屬于前一個(gè)問(wèn)題的完善，意在引發(fā)學(xué)生感知數(shù)學(xué)的嚴(yán)謹(jǐn)性；第三個(gè)問(wèn)題著重引發(fā)學(xué)生對(duì)自變量t的變化范圍產(chǎn)生關(guān)注，并用標(biāo)準(zhǔn)化的語(yǔ)言進(jìn)行描述，以訓(xùn)練學(xué)生的表達(dá)能力.

活動(dòng)2 已知某公司確定的工資標(biāo)準(zhǔn)是每人每天350元，工資周付，要求工人每周工作最多6天，最少不低于1天.

問(wèn)題1：工人每周可獲取多少工資？

問(wèn)題2：工人工資w與天數(shù)d之間存在什么關(guān)系？屬于函數(shù)關(guān)系嗎？說(shuō)明理由.

問(wèn)題3：嘗試準(zhǔn)確表達(dá)工資w與天數(shù)d的關(guān)系.

追問(wèn)：以上兩個(gè)活動(dòng)可以表示成一樣的函數(shù)關(guān)系嗎？為什么？（要求學(xué)生獨(dú)立思考，自主回答. ）

設(shè)計(jì)意圖 學(xué)生經(jīng)歷過(guò)活動(dòng)1的探索，對(duì)此類問(wèn)題已經(jīng)具備一定的獨(dú)立思考能力. 活動(dòng)2的設(shè)計(jì)一方面夯實(shí)學(xué)生對(duì)此類問(wèn)題的認(rèn)識(shí)基礎(chǔ)，另一方面強(qiáng)化學(xué)生對(duì)值域、定義域的認(rèn)識(shí).

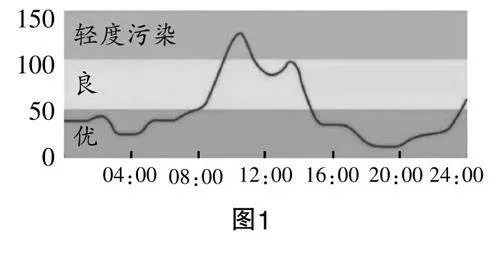
活動(dòng)3 圖1是某市某天的空氣質(zhì)量指數(shù)（簡(jiǎn)稱AQI）變化圖.

問(wèn)題1：觀察圖示，是否能確定這一天內(nèi)任一時(shí)刻t h的AQI的值I？

問(wèn)題2：此處的I為t的函數(shù)嗎？說(shuō)明理由.

追問(wèn)1：中午12時(shí)的AQI的值是多少？該值是唯一的嗎？

追問(wèn)2：數(shù)集A=｛t0≤t≤24｝中的任意值t，可用什么方法探尋與之對(duì)應(yīng)的值I？

（小組合作，幾何畫板演示，揭露對(duì)應(yīng)關(guān)系. ）

設(shè)計(jì)意圖 該活動(dòng)探究的是某一時(shí)刻所對(duì)應(yīng)的AQI的值，在此之前學(xué)生所了解的函數(shù)基本是用解析式呈現(xiàn)的，對(duì)用圖象描述相應(yīng)關(guān)系的接觸較少，尤其在無(wú)法確定值域的情況下，令學(xué)生感到困惑.

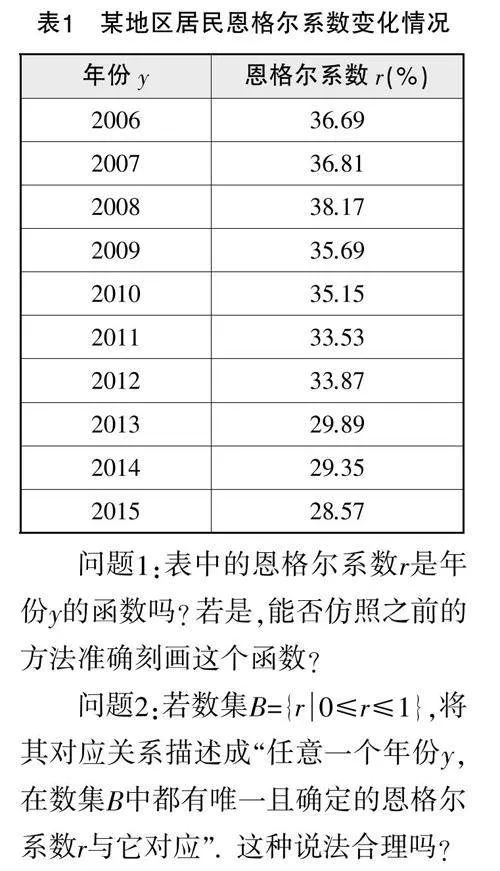
活動(dòng)4 r=×100%為恩格爾系數(shù)，國(guó)際上常以此來(lái)研究某個(gè)地區(qū)人民的生活質(zhì)量. 如表1所示，此為我國(guó)某地區(qū)居民恩格爾系數(shù)變化情況.

問(wèn)題1：表中的恩格爾系數(shù)r是年份y的函數(shù)嗎？若是，能否仿照之前的方法準(zhǔn)確刻畫這個(gè)函數(shù)？

問(wèn)題2：若數(shù)集B=｛r0≤r≤1｝，將其對(duì)應(yīng)關(guān)系描述成“任意一個(gè)年份y，在數(shù)集B中都有唯一且確定的恩格爾系數(shù)r與它對(duì)應(yīng)”. 這種說(shuō)法合理嗎？

設(shè)計(jì)意圖 基于上述三個(gè)活動(dòng)，學(xué)生對(duì)于借助表格理解對(duì)應(yīng)關(guān)系已經(jīng)有了一定基礎(chǔ)，但仍有一些困惑. 教師借此機(jī)會(huì)引發(fā)學(xué)生思考，讓學(xué)生對(duì)值域的合理性有更明確的認(rèn)識(shí).

綜上四個(gè)活動(dòng)，都以學(xué)生的生活背景為原材料設(shè)計(jì)問(wèn)題，引發(fā)學(xué)生對(duì)函數(shù)中的“對(duì)應(yīng)關(guān)系與定義域”產(chǎn)生明確的認(rèn)識(shí). 隨著追問(wèn)的提出與解決，學(xué)生對(duì)函數(shù)的概念形成了初步了解，并學(xué)會(huì)從集合的角度來(lái)描述值域與定義域，凸顯了數(shù)學(xué)學(xué)科的嚴(yán)謹(jǐn)性. 學(xué)生也從中感知到知識(shí)間密不可分的關(guān)系，整個(gè)教學(xué)活動(dòng)為接下來(lái)的教學(xué)奠定了基礎(chǔ).

2. 過(guò)程階段——辨析概念

問(wèn)題1：回顧以上探究活動(dòng)，嘗試總結(jié)它們的共同點(diǎn).

問(wèn)題2：如何表述函數(shù)的概念？

問(wèn)題3：函數(shù)的解析式一定是y=f（x）嗎？

問(wèn)題4：類比初中階段所了解的函數(shù)概念，是否有新的發(fā)現(xiàn)？

設(shè)計(jì)意圖 問(wèn)題1帶領(lǐng)學(xué)生體會(huì)用集合及對(duì)應(yīng)關(guān)系來(lái)刻畫函數(shù)，經(jīng)歷從特殊到一般的過(guò)程，體驗(yàn)創(chuàng)造的愉悅；問(wèn)題2的提出，意在引導(dǎo)學(xué)生用邏輯清晰及規(guī)范化的語(yǔ)言來(lái)表達(dá)相應(yīng)的信息；問(wèn)題3是教學(xué)重點(diǎn)與難點(diǎn)，y=f（x）為抽象的數(shù)學(xué)符號(hào)，學(xué)生需要理解其實(shí)際含義；問(wèn)題4是對(duì)初中“變量說(shuō)”的進(jìn)一步深化，讓學(xué)生理解“對(duì)應(yīng)說(shuō)”，以擴(kuò)大學(xué)生的研究范圍.

此環(huán)節(jié)，教師通過(guò)問(wèn)題驅(qū)動(dòng)與變式引導(dǎo)的方式，促使學(xué)生回顧活動(dòng)階段中的內(nèi)容，以提取準(zhǔn)確有效的信息，讓學(xué)生自主產(chǎn)生用集合表示函數(shù)的意識(shí)，此為對(duì)函數(shù)概念產(chǎn)生初步了解的過(guò)程，為接下來(lái)的歸納總結(jié)奠定基礎(chǔ).

3. 對(duì)象階段——鞏固、應(yīng)用概念

要求學(xué)生分別說(shuō)一說(shuō)正比例函數(shù)y=kx（k≠0）、反比例函數(shù)y=（k≠0）、一次函數(shù)y=kx+b（k≠0）、二次函數(shù)y=ax2+bx+c（a≠0）的定義域、值域以及對(duì)應(yīng)關(guān)系. 在此基礎(chǔ)上，要求學(xué)生談一談圖2所表示的y為x的函數(shù)關(guān)系有哪些.

設(shè)計(jì)意圖 帶領(lǐng)學(xué)生重新認(rèn)識(shí)已經(jīng)接觸過(guò)的簡(jiǎn)單函數(shù)，并通過(guò)圖象回顧函數(shù)的定義，深化學(xué)生對(duì)“定義域、值域與對(duì)應(yīng)關(guān)系”三要素的理解.

關(guān)于區(qū)間概念的教學(xué)，教師可提供一張表格，要求學(xué)生根據(jù)區(qū)間的概念，自主從定義、區(qū)間名稱、符號(hào)與數(shù)軸等方面展開(kāi)分析，體會(huì)集合與區(qū)間的關(guān)系，感知數(shù)學(xué)獨(dú)有的簡(jiǎn)約美. 當(dāng)學(xué)生對(duì)概念有了充分了解后，教師可擇取一些具有代表意義的例題與學(xué)生共同探索.

例1 若函數(shù)f（x）=+.

（1）求該函數(shù)的定義域；

（2）求f（-3）與f

的值；

（3）若a>0，則f（a）與f（a-1）的值分別是多少？

設(shè)計(jì)意圖 學(xué)生接觸得比較多的是函數(shù)的解析式，對(duì)于函數(shù)的定義域（讓解析式有意義的實(shí)數(shù)集合）并沒(méi)有特別強(qiáng)調(diào). 此例意在促使學(xué)生學(xué)會(huì)從隱含條件出發(fā)解決問(wèn)題，理解當(dāng)明確自變量與解析式時(shí)，該如何求得函數(shù)值.

對(duì)象階段的教學(xué)，教師結(jié)合概念與非概念變式，帶領(lǐng)學(xué)生將函數(shù)的概念提煉為具體的思維. 此環(huán)節(jié)，教師首先帶領(lǐng)學(xué)生從熟悉的正比例、反比例、一次函數(shù)與二次函數(shù)出發(fā)，深化學(xué)生對(duì)函數(shù)三要素的理解；其次通過(guò)設(shè)計(jì)例題促使學(xué)生學(xué)會(huì)應(yīng)用建構(gòu)的函數(shù)概念來(lái)解決實(shí)際問(wèn)題，讓概念一一對(duì)應(yīng)的形態(tài)根植于學(xué)生的認(rèn)知結(jié)構(gòu).

4. 圖式階段——拓展、總結(jié)概念

例2 已知函數(shù)f（x）=5x2+2x.

（1）求f（a）+f（-a）的值；

（2）f（x）的值域是什么？

變式題1：已知函數(shù)f（x）=5x2+2x，當(dāng)x>5時(shí)，值域是什么？當(dāng)x∈｛-4，-3，-2，-1，0，1，2，3，4｝時(shí)，值域是什么？

變式題2：已知函數(shù)f（x）=5x2+2x，值域?yàn)椋?2，13］，定義域是什么？若值域?yàn)椋?4，-2，4，8｝，則定義域是什么？

設(shè)計(jì)意圖 將函數(shù)的概念有機(jī)地融入變式題組內(nèi)，促使學(xué)生形成良好的心理圖式，進(jìn)一步深化學(xué)生對(duì)函數(shù)概念的認(rèn)識(shí)，并引導(dǎo)學(xué)生應(yīng)用函數(shù)的概念來(lái)解決實(shí)際問(wèn)題.

師：本節(jié)課的學(xué)習(xí)給你帶來(lái)了什么收獲與感悟？

設(shè)計(jì)意圖 此為課堂小結(jié)部分，引導(dǎo)學(xué)生從概念的本質(zhì)、內(nèi)涵、要素等方面出發(fā)，回顧整個(gè)學(xué)習(xí)過(guò)程，從關(guān)鍵詞的角度進(jìn)一步完善函數(shù)的概念，建構(gòu)完整的知識(shí)網(wǎng)絡(luò).

圖式階段為前三個(gè)階段的融合，涉及的變式題有分解與逆向兩種. 在該階段中，學(xué)生已經(jīng)能將新建構(gòu)的概念納入認(rèn)知體系內(nèi)，隨著對(duì)概念的反復(fù)應(yīng)用，學(xué)生對(duì)概念的理解更加深刻. 該階段相對(duì)靈活，教師需要結(jié)合學(xué)情設(shè)計(jì)一些梯度明顯的小問(wèn)題與變式題來(lái)啟發(fā)學(xué)生的思維，提升學(xué)生的解題能力.

總之，APOS理論與變式教學(xué)理論有機(jī)地融合于概念教學(xué)，不僅讓課堂教學(xué)更加井然有序，還讓學(xué)生的思維環(huán)環(huán)相扣，在循序漸進(jìn)的問(wèn)題中逐漸深入. 因此，這是一種值得探索的教學(xué)方式，對(duì)促進(jìn)學(xué)生全面發(fā)展具有重要價(jià)值與意義.