關于“距離的計算”章節知識內容的教學指導與思考

[摘 要] 教學“距離的計算”章節知識內容時,要注意知識整合,采用活動探究的方式,引導學生經歷知識的探究和應用過程,幫助學生掌握程序性解法. 文章就此開展教學探究,提出相應的教學建議.
[關鍵詞] 距離的計算;教學;活動;應用
“距離的計算”是高中數學的重要章節知識內容,是“空間向量與立體幾何”的重要知識內容的組成. 該部分教學需要教師指導學生掌握空間距離的計算方法,強化學生的空間幾何觀,提升學生的數學素養. 因此,教學中需要整合知識內容,精設教學環節,合理引導學生探究. 下面結合實踐展開敘述.
整合內容,策略探究
向量是數學中特殊的“量”,其具有大小和方向,故具有代數與幾何雙重特性,因此可作為溝通代數與幾何的橋梁,用于解決代數與幾何問題. 本章節教學中,需要將空間向量作為解析三維空間中圖形的位置關系與數量關系的重要工具.
1. 內容整合
教學“距離的計算”章節知識內容時,可將其分為兩部分:一是點到直線的距離,以及兩平行線間的距離;二是點到平面的距離,以及兩平行面間的距離. 學生在學習時已經掌握了空間向量的相關知識,在此基礎上深入探索用空間向量解決距離問題的方法.
如圖1所示,“空間向量的定義及其運算”“用空間向量表示點、直線、平面等元素”“建立空間圖形與空間向量的聯系”是探究學習“距離的計算”的三大基礎知識,需要指導學生重點掌握.
教學中需要明晰知識間的關系,利用知識網來定位本章節的知識內容. 對于其中的關系網,需要關注兩條關系鏈:一是利用“空間向量的定義及其運算”構建“空間向量運算的幾何表示”,從而利用空間向量運算解決空間距離問題;二是利用“空間向量的定義及其運算”構建“空間向量運算的坐標表示”,后續應用該知識解決空間距離問題.
教學中需要明確如下三大任務目標:一是引導學生歸納空間中的四類距離向量表示方法(空間中點到直線的距離、兩平行線間的距離、點到平面的距離、兩平行面間的距離的向量表示);二是引導學生利用空間向量解決立體幾何距離問題,總結程序性解題方法;三是滲透數學思想,培養學生應用意識.
2. 策略探究
對于“距離的計算”知識內容的教學,建議以問題為導向,驅動課堂探究. 教師要關注學生的思維活動,引導學生探究、合作、交流、思考,鼓勵學生質疑、討論、展示,參與課堂的探究活動,經歷知識的生成過程.
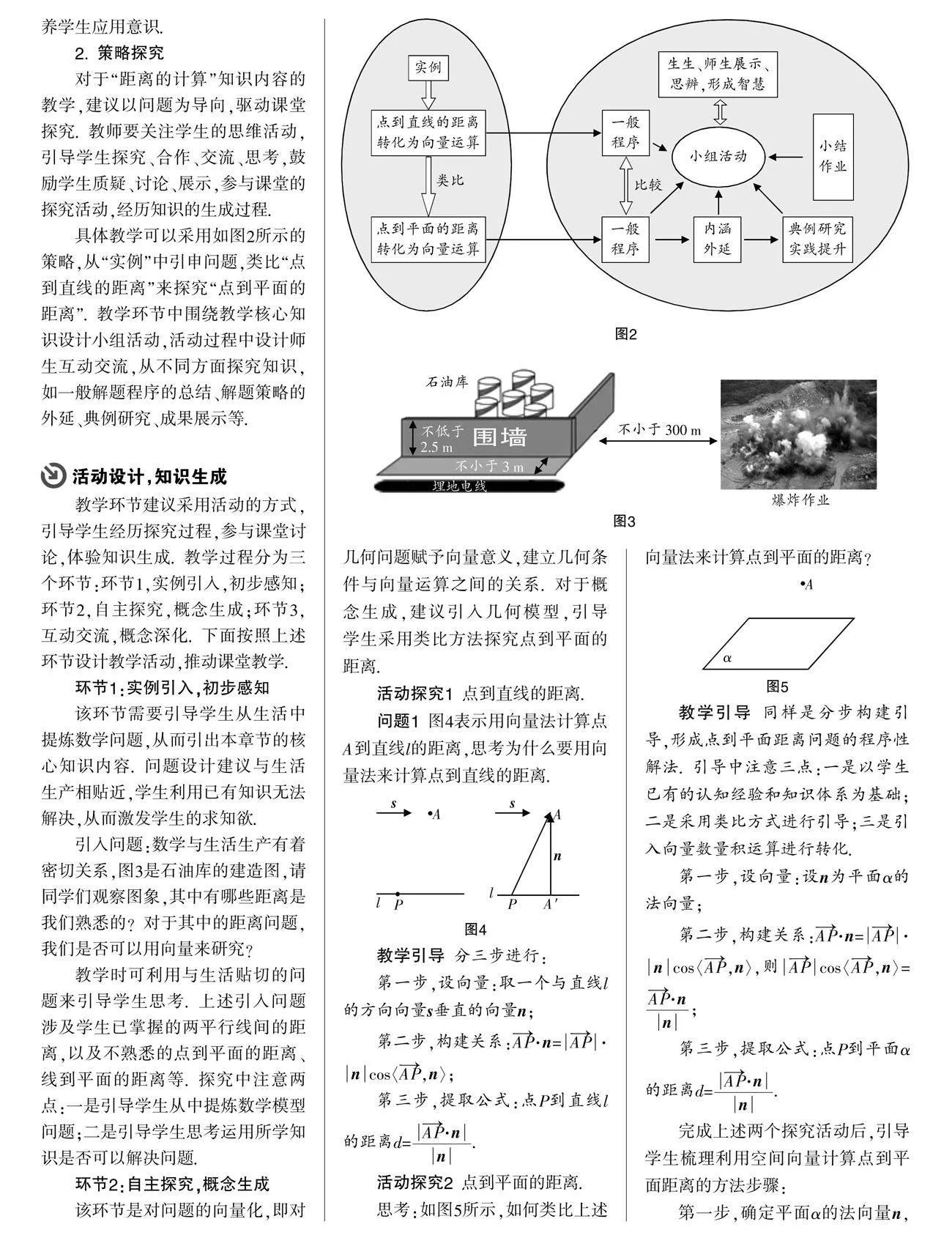
具體教學可以采用如圖2所示的策略,從“實例”中引申問題,類比“點到直線的距離”來探究“點到平面的距離”. 教學環節中圍繞教學核心知識設計小組活動,活動過程中設計師生互動交流,從不同方面探究知識,如一般解題程序的總結、解題策略的外延、典例研究、成果展示等.
活動設計,知識生成
教學環節建議采用活動的方式,引導學生經歷探究過程,參與課堂討論,體驗知識生成. 教學過程分為三個環節:環節1,實例引入,初步感知;環節2,自主探究,概念生成;環節3,互動交流,概念深化. 下面按照上述環節設計教學活動,推動課堂教學.
環節1:實例引入,初步感知
該環節需要引導學生從生活中提煉數學問題,從而引出本章節的核心知識內容. 問題設計建議與生活生產相貼近,學生利用已有知識無法解決,從而激發學生的求知欲.
引入問題:數學與生活生產有著密切關系,圖3是石油庫的建造圖,請同學們觀察圖象,其中有哪些距離是我們熟悉的?對于其中的距離問題,我們是否可以用向量來研究?
教學時可利用與生活貼切的問題來引導學生思考. 上述引入問題涉及學生已掌握的兩平行線間的距離,以及不熟悉的點到平面的距離、線到平面的距離等. 探究中注意兩點:一是引導學生從中提煉數學模型問題;二是引導學生思考運用所學知識是否可以解決問題.
環節2:自主探究,概念生成
該環節是對問題的向量化,即對幾何問題賦予向量意義,建立幾何條件與向量運算之間的關系. 對于概念生成,建議引入幾何模型,引導學生采用類比方法探究點到平面的距離.
活動探究1 點到直線的距離.
問題1 圖4表示用向量法計算點A到直線l的距離,思考為什么要用向量法來計算點到直線的距離.
第三步,提取公式:點P到平面α的距離d=.
完成上述兩個探究活動后,引導學生梳理利用空間向量計算點到平面距離的方法步驟:
第一步,確定平面α的法向量n,選擇參考向量;
第二步,構建向量在法向量n上的投影向量;
第三步,結合向量數量積公式計算投影向量的長度.
環節3:互動交流,概念深化
環節3需要對概念和程序性解法進行深化,教學中引導學生進行互動交流,觀察實例模型,從中體驗向量法的優點.
活動1 互動交流.
請學生分享利用向量法計算點到直線的距離、點到平面的距離的感想,以及使用向量法時需要注意哪些要素.
活動2 實例感悟.
請學生觀察圖6中的圖形,然后從不同視角思考:使用向量法有哪些優勢?
教學引導 教學中進一步挖掘向量法的本質內涵,同時借用不同的實例模型進行向量法的拓展與外延,讓學生思考其他解決點到平面的距離問題的方法,對比感悟向量法的優勢點. 教學中注意給學生留足思考空間,讓學生分組互動討論,分享成果,親身體會.
運用探究,解題指導
“運用探究,解題指導”是“距離的計算”章節知識內容的重要教學環節,該環節教學需要結合實例引導學生分析探究,過程中要注意三點:一是深度分析問題,把握問題特征;二是引導學生思考問題解法;三是解題過程指導,引導學生剖析解法策略.
問題呈現 如圖7所示,已知正方體ABCD-ABCD的棱長為2,E,F分別為上底面ABCD和側面CDDC的中心,則點C到平面AEF的距離為______.
教學引導 教學中需要引導學生靈活運用程序性解法來求解點C到平面AEF的距離,可分三個階段進行引導探究. 第一階段,問題條件分析;第二階段,過程分步構建;第三階段,解后反思總結.
第一階段,問題條件分析.
(1)對于上述問題,可將其歸為哪種類型?
(2)上述問題有什么特點?核心條件有幾個?應采用怎樣的解題方法?
第二階段,過程分步構建.
先根據特征建立空間直角坐標系,然后利用向量法,按照解題程序步驟求解.
第一步,建立空間直角坐標系.
如圖8所示,以點A為原點,AB,AD,AA所在直線為x,y,z軸建立空間直角坐標系,易得A(0,0,0),E(1,1,2),F(1,2,1),C(2,2,0).
教學引導 教學中引導學生思考如何建立空間直角坐標系更為便捷(從點坐標設定、幾何特性等視角進行引導). 完成空間直角坐標系的建立后,讓學生結合線段長自行求解點的空間坐標.
第二步,求解平面的法向量.
設平面AEF的法向量為n=(x,y,z),則n
·=x+y+2z=0,
n
·=x+2y+z=0.令y=-1,可得n=(3,-1,-1).
教學引導 該步需要引導學生關注兩點:一是利用向量數量積構建方程求解平面的法向量;二是理解平面的法向量并不唯一,可以按要求隨意設定.
第三步,利用距離公式求解.
結合點到平面的距離的向量公式可知,點C到平面AEF的距離為==.
教學引導 該步是本章節核心知識的體現,需要引導學生靈活運用. 教學中要讓學生關注兩點:一是公式中每一個要素所代表的含義與幾何量;二是求出結果后,慎重思考是否滿足題意.
第三階段,解后反思總結.
問題求解后,引導學生反思過程與方法. 可從三個方面引導學生反思:①對于上述問題,還有其他解法嗎?②對于上述向量法,第二步運用了向量的哪些幾何性質?③若用向量法求解直線到平面的距離,應如何構建過程?
教學中引導學生深入思考,反思過程與方法,強化解法,拓展應用,掌握該類問題的解法策略. 必要時可以設置拓展性問題,引導學生思考更加深入.
總之,對于“距離的計算”章節知識內容的教學,需要慎重處理三大模塊:整合知識內容,確定探究策略;合理設計探究活動,引發知識自然生成;總結問題的程序性解法,綜合運用,強化解法. 整個教學環節,充分引導學生參與課堂討論,讓學生在活動中感悟知識、內化知識. 同時注意合理滲透數學思想方法,發展學生的數學學科核心素養.

