“圓”潤生活

命題者在命制中考試題時，通常會把圓的知識點與生產生活中的一些場景結合起來，這樣既能考查同學們對圓的知識點的掌握情況，又能考查同學們應用知識解決實際問題的能力。解決這類問題的關鍵是準確地把實際問題轉化為數學問題。

一、圓周角定理的應用

例1 如圖1，某博覽會上有一圓形展示區，在其圓形邊緣的點P處安裝了一臺監視器，它的監控角度是55°。為了監控整個展示區，最少需要在圓形邊緣上共安裝這樣的監視器 臺。

【解析】本題考查了圓周角定理“在同圓或等圓中，同弧或等弧所對的圓周角相等，都等于這條弧所對的圓心角的一半”。一臺監視器的監控角度是55°，也就是告訴我們，圓周角是55°，那么圓周角所對的弧所對的圓心角是110°。要想監控整個圓形展示區，安裝的監視器對應的圓心角至少為360°。因為360°÷110°=[3311]， 所以最少需要在圓形邊緣上共安裝這樣的監視器4臺。

二、垂徑定理的應用

例2 筒車是我國古代發明的一種水利灌溉工具，明朝科學家徐光啟在《農政全書》中用圖畫描繪了筒車的工作原理，如圖2。筒車盛水桶的運行軌道是以軸心O為圓心的圓，如圖3，已知圓心O在水面上方，且⊙O被水面截得的弦AB長為6米，⊙O半徑長為4米。若點C為運行軌道的最低點，則點C到弦AB所在直線的距離是（ ）。

A.1米 B.（4-[7]）米

C.2米 D.（4+[7]）米

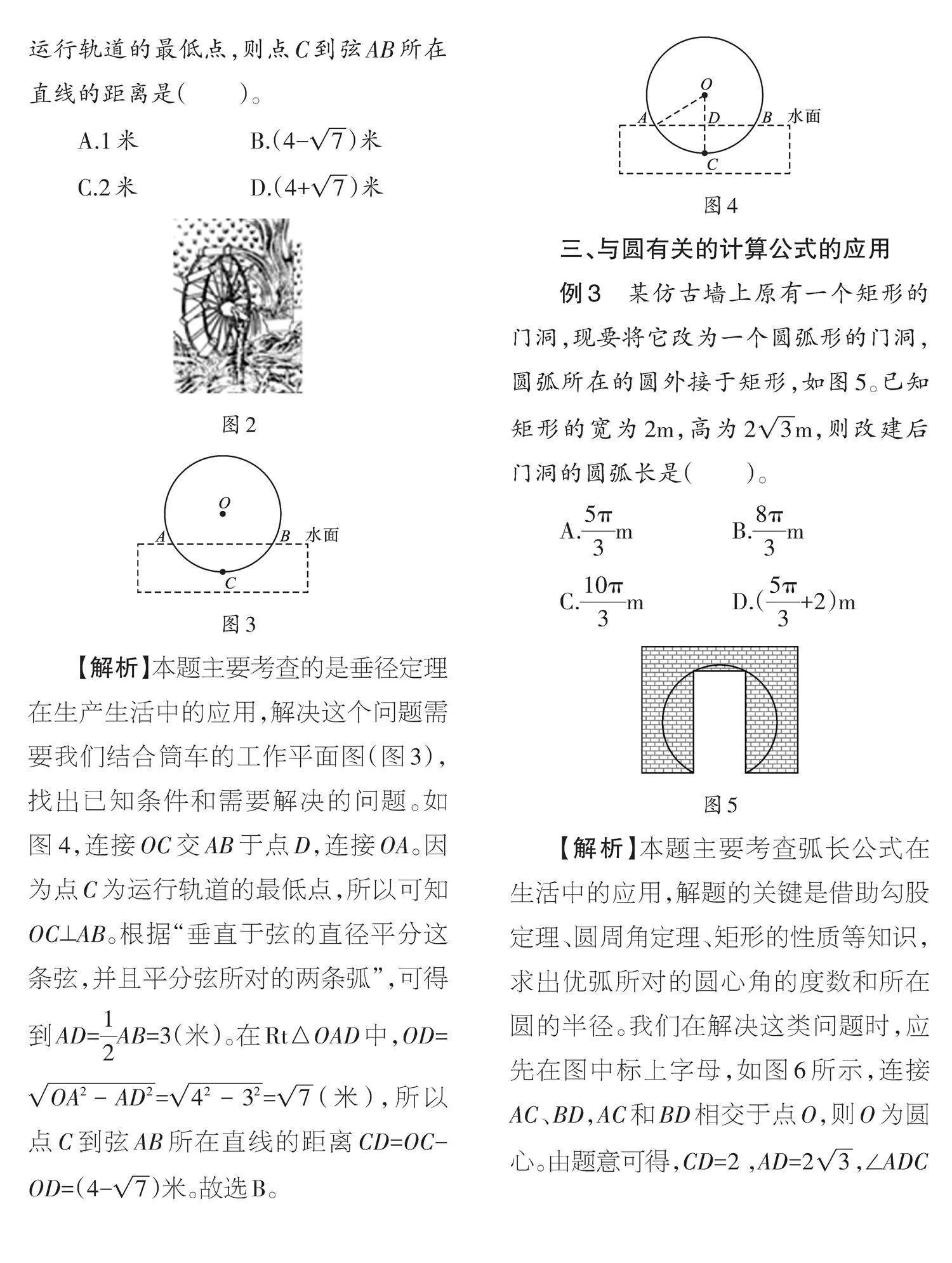
【解析】本題主要考查的是垂徑定理在生產生活中的應用，解決這個問題需要我們結合筒車的工作平面圖（圖3），找出已知條件和需要解決的問題。如圖4，連接OC交AB于點D，連接OA。因為點C為運行軌道的最低點，所以可知OC⊥AB。根據“垂直于弦的直徑平分這條弦，并且平分弦所對的兩條弧”，可得到AD=[12]AB=3（米）。在Rt△OAD中，OD=[OA2-AD2]=[42-32]=[7]（米），所以點C到弦AB所在直線的距離CD=OC-OD=（4-[7]）米。故選B。

三、與圓有關的計算公式的應用

例3 某仿古墻上原有一個矩形的門洞，現要將它改為一個圓弧形的門洞，圓弧所在的圓外接于矩形，如圖5。已知矩形的寬為2m，高為[23]m，則改建后門洞的圓弧長是（ ）。

A.[5π3]m B.[8π3]m

C.[10π3]m D.（[5π3]+2）m

【解析】本題主要考查弧長公式在生活中的應用，解題的關鍵是借助勾股定理、圓周角定理、矩形的性質等知識，求出優弧所對的圓心角的度數和所在圓的半徑。我們在解決這類問題時，應先在圖中標上字母，如圖6所示，連接AC、BD，AC和BD相交于點O，則O為圓心。由題意可得，CD=2 ，AD=[23]，∠ADC

=90°，所以tan∠DCA=[ADCD]=[232]=[3]，AC=[CD2+AD2]=4，進而可求得∠ACD=60°，OA=OC=2。所以可求得優弧ADB所對的圓心角為300°。所以改建后門洞的圓弧長為[300π×2180]=[10π3]（m）。故選C。

四、與圓有關的位置關系的應用

例4 （多選）發動機的曲柄連桿將直線運動轉化為圓周運動，圖7是其示意圖。圖7中，點A在直線l上往復運動，推動點B做圓周運動形成⊙O，AB與BO表示曲柄連桿的兩直桿，點C、D是直線l與⊙O的交點。當點A運動到點E時，點B到達點C；當點A運動到點F時，點B到達點D。若AB=12，OB=5，則下列結論正確的是（ ）。

A.FC=2

B.EF=12

C.當AB與⊙O相切時，EA=4

D.當OB⊥CD時，EA=AF

【解析】本題主要考查的是圓的切線的性質在生產生活中的應用，解決這個問題的關鍵是對“發動機的曲柄連桿將直線運動轉化為圓周運動”的理解。由題意可得AB=CE=12，AB+BO=OE=17，FD=AB=12，OC=OB=OD=5，從而可判斷選項A正確，選項B不正確；當AB與⊙O相切時，∠ABO=90°，由勾股定理可求得AO=13，所以EA=EO-AO=17-13=4，則選項C正確；當OB⊥CD時，由勾股定理可求得AO=[119]，所以AE=EO-AO=17-[119]，AF=AO-OF=[119]-2-5=[119]-7，所以AE≠AF，故選項D不正確。故應選擇AC。

（作者單位：江蘇省泰州市姜堰區實驗初級中學）