利用導數法解雙變量含參函數的“任意性”問題


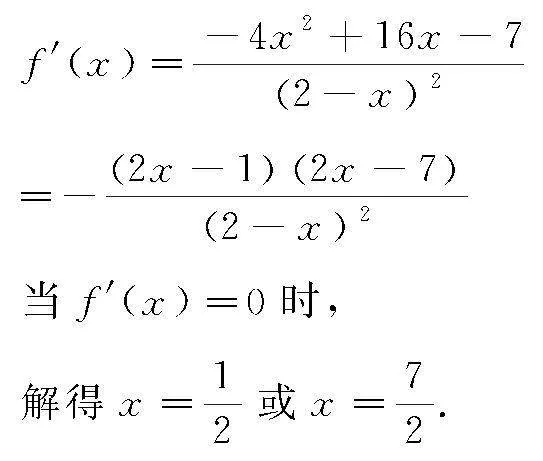

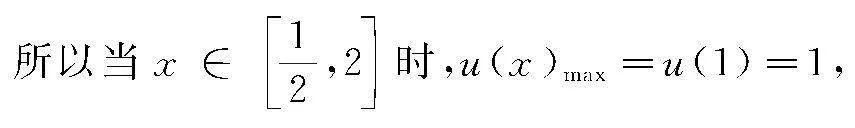


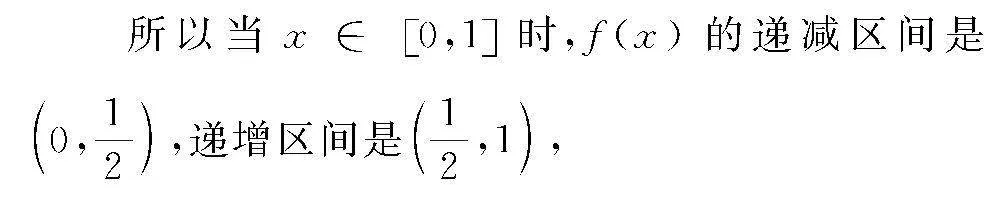
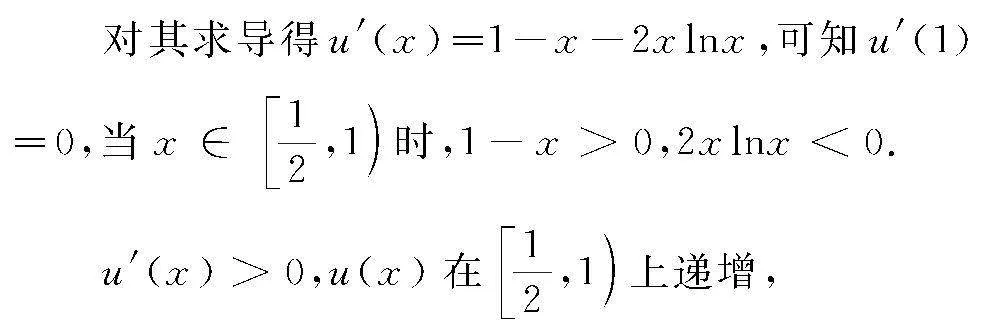
【摘要】導數法是解函數問題最基本的方法之一,在求函數的單調區間、極值、最值等問題上有著重要應用.雙變量含參函數的“任意性”問題是高中數學的難點問題,考查學生對轉化思想與函數思想的綜合運用,其解答過程通常會涉及求函數的單調區間、極值、最值等.本文對利用導數法解雙變量含參函數的“任意性”問題進行解題分析,以期幫助學生在解答這類問題時更加熟練.
【關鍵詞】導數法;高中數學;解題技巧
1 “任意=存在”型問題
解 (1)根據題意有
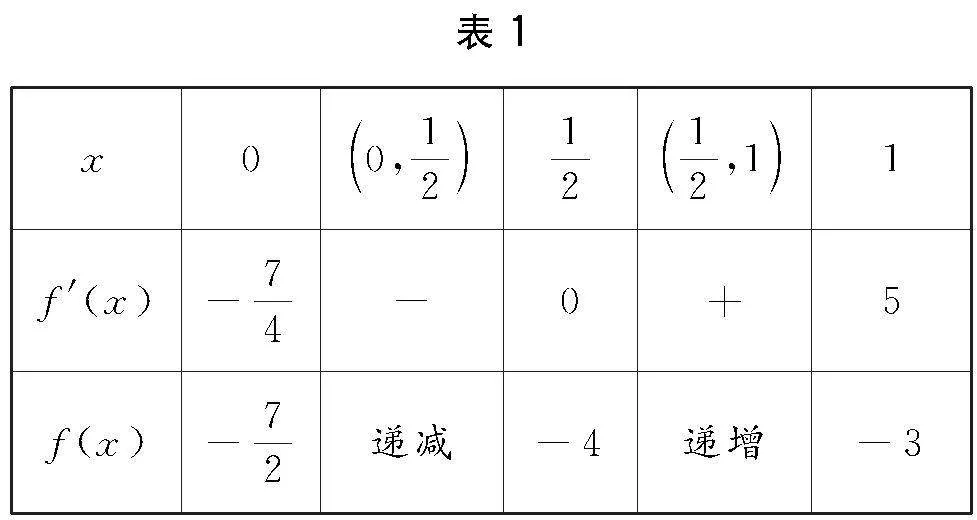
當x變化時,f′(x),f(x)的變化情況如表1.
f(x)min=-4,f(x)max=-3,
故f(x)的值域為-4,-3.
(2)設函數g(x)的值域為A,函數f(x)的值域為B.
因為a≥1,
所以當x∈0,1時,g′(x)=3(x2-a2)≤0.
所以當x∈0,1時,g(x)為單調減函數,
則g(x)的值域A=1-2a-3a2,-2a.
又由(1)知B=-4,-3,
點評 等價轉化思想指的是在數學問題中,通過變形、化簡或者轉化等方法,將原問題轉化為一個與之等價的形式,從而更容易求解或者理解.本題的等價轉化的基本思想就是:函數f(x)的值域為函數g(x)值域的子集.
2 “任意≥(≤)任意”型問題
即a≥x-x2lnx,
設u(x)=x-x2lnx,
當x∈1,2時,1-x<0,2xlnx>0,
u′(x)<0,u(x)在1,2上遞減.
所以a的取值范圍是1,+∞.
點評 對于“任意≥(≤)任意”型問題,其轉化的思考過程如下:
3 結語
利用導數解決雙變量函數的“任意性”問題,轉化是解題的關鍵.思考過程一般是將等式或不等式成立問題轉化為函數的最值問題,利用導數求出函數的最值,再根據題目要求對所求的最值進行大小比較,從而求得參數的取值范圍.這一過程有時也會用到分離參數法,先將參數與函數進行分離,再用導數法求最值,需隨機應變.
參考文獻:
[1]朱禮強.如何運用導數法解答函數問題[J].語數外學習(高中版上旬),2023(01):59-60.
[2]吳春霞.摭談巧用導數法解不等式恒成立問題[J].中學數學教學參考,2022(03):49-51.
[3]王玉瑩.導數法處理不等式恒成立問題的幾種簡化思維[J].高中數理化,2023(15):67-68.

