三角形場景創設,誘導公式妙應用

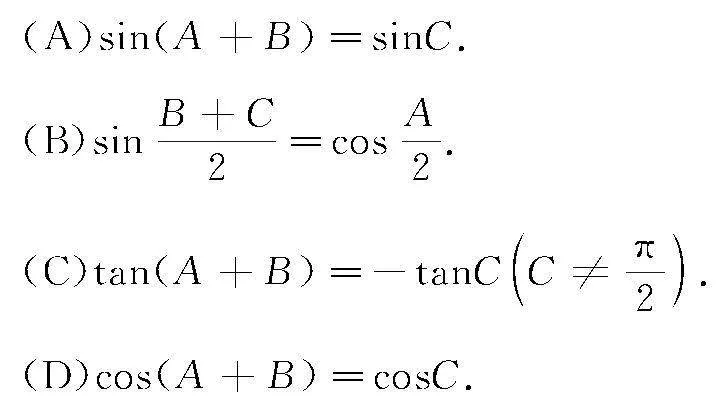
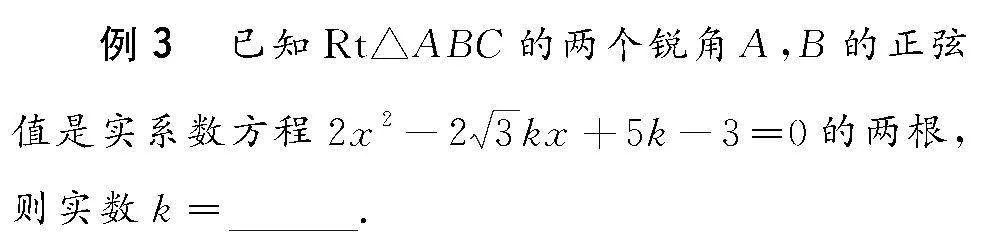

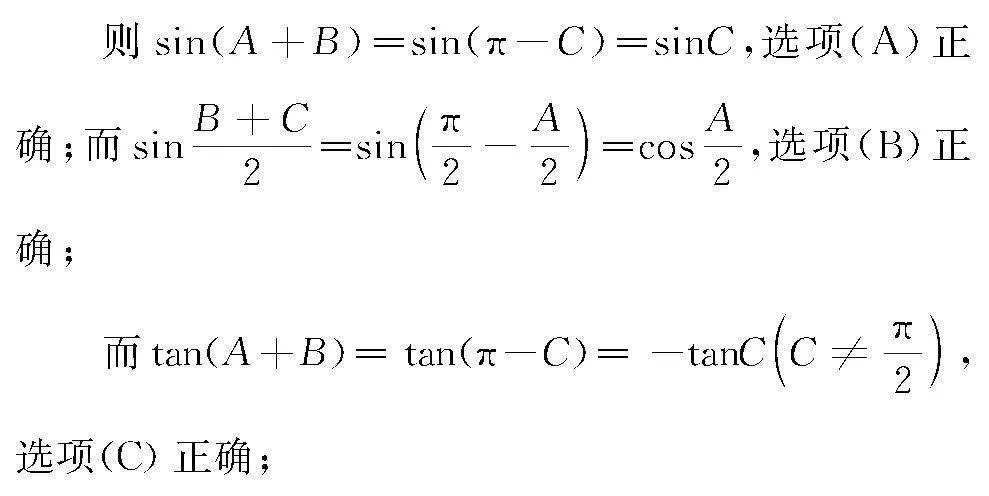
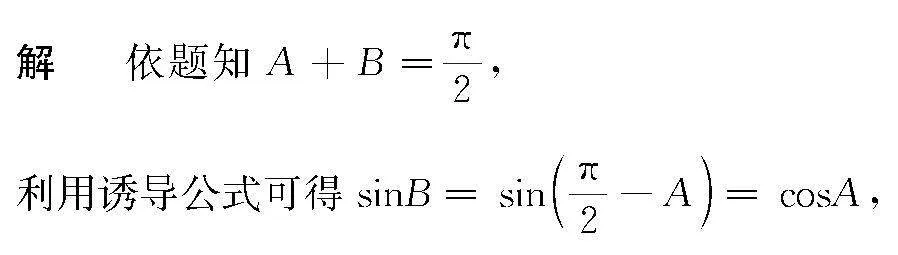

【摘要】誘導公式是三角函數中的一類基本公式,對于三角關系式的化簡、求值以及證明等都有特殊的應用.而以三角形為場景的三角函數問題,對于誘導公式的應用更加靈活多變,巧妙融入三角形的內角和公式以及相關的性質,在多種情況下都有重要作用,可引領并指導數學教學與應用.
【關鍵詞】高中數學;三角函數;誘導公式
誘導公式巧妙揭示了終邊具有某些對稱關系的兩個角的三角函數之間的關系,可以有效地將終邊對稱的圖形關系直觀地“翻譯”成三角函數之間的代數關系,對于三角函數中的化簡、求值、證明等相關問題的應用有實效.同時,誘導公式也巧妙地將函數與方程、不等式、幾何問題等聯系起來,成為三角函數知識考查中的一個基本點.利用誘導公式處理與解決一些與三角形相關的問題,備受各方關注.
1 命題的判斷
在三角形中,借助三角形的基本性質,結合誘導公式的應用,可以用來判斷一些涉及三角函數式的變換與應用問題.此類場景中,往往基于三角形背景來判斷一些三角關系式是否成立.
例1 (多選題)已知A,B,C為△ABC的三個內角,下列結論正確的是( )
分析 根據題設條件,利用三角形的內角和定理構建關系式A+B+C=π,代入各選項中,利用對應的誘導公式加以分析與應用,進而對比各選項中結論的真假.
解 在△ABC中,由三角形的內角和定理有A+B+C=π,
而cos(A+B)=cos(π-C)=-cosC,選項(D)錯誤;
故選擇答案:(A)(B)(C).
點評 在具體判斷三角函數關系式是否成立時,基于三角形的內角和定理,合理代換處理,充分利用誘導公式加以變形與轉化,有效減少角的個數,方便三角關系式的變形或化簡,為三角關系式是否成立的判斷提供條件.
2 等式的證明
在三角形中,有關三角形中相關角的三角函數式的證明與應用問題,離不開三角形的基本性質與誘導公式的應用.此類場景中,往往基于三角形背景證明一些內角之間的代數關系或內角的三角函數值之間的關系式成立等.
例2 已知A,B,C為△ABC的三個內角,且滿足sinC=sinB(1+2cosA),試證明:A=2B.
分析 根據題設條件,利用三角形的內角和定理,并結合誘導公式的應用對題設三角關系式進行變形,結合三角恒等變換公式的應用,得到sinB=sin(A-B),進而分兩種情況加以分類討論.
證明 由三角形的內角和定理有A+B+C=π,
則有sinC=sinπ-(A+B)=sin(A+B),
依題可得sinC=sinB(1+2cosA)=sin(A+B),
所以sinB+2sinBcosA=sinAcosB+cosAsinB,
整理有sinB=sinAcosB-cosAsinB,
可得sinB=sin(A-B),
則有B=A-B或B+(A-B)=π,
可得A=2B或A=π(舍去),
所以A=2B成立.
3 參數的求值
在三角形中,涉及與之相關的含參函數與方程、不等式等問題,經常借助三角形的基本性質、同角三角函數基本關系式以及誘導公式等的綜合應用來分析求解.此類場景中,往往基于三角形背景設置方程的根與應用等.
分析 根據題設條件,利用直角三角形的結構特征構建兩銳角的關系式,并結合誘導公式建立三角關系式,同時利用方程的根的條件以及韋達定理構建關系式,利用平方和的關系轉化為涉及含參數的二次方程,利用方程的求解以及分類討論驗證確定參數的值.
則有sin2A+sin2B=sin2A+cos2A=1,
所以(sinA+sinB)2=sin2A+sin2B+2sinAsinB=1+5k-3=3k2,
整理有3k2-5k+2=0,
點評 在解決涉及三角形中的函數與方程問題時,要綜合考慮三角形的基本性質,以及函數與方程的基本知識.如該問題中二次方程有根的判別式條件,以及對應的三角函數值的取值在范圍0,1內,等等,都是題目的隱含條件,在實際解題過程中要加以充分考慮與分析應用.
4 結語
利用誘導公式解決三角形場景下的綜合問題,關鍵是合理把握三角形的基本性質,正確應用誘導公式的相應規律,同時要注意三角形中各內角均為(0,π)上的角,以及三角形的三個內角和為π這些條件的限制,將其綜合起來加以分析與研究.

