求解一類時(shí)間分?jǐn)?shù)階擴(kuò)散方程的深度學(xué)習(xí)方法

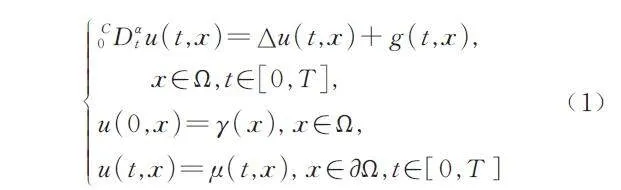
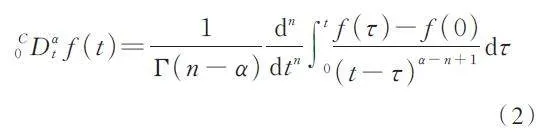
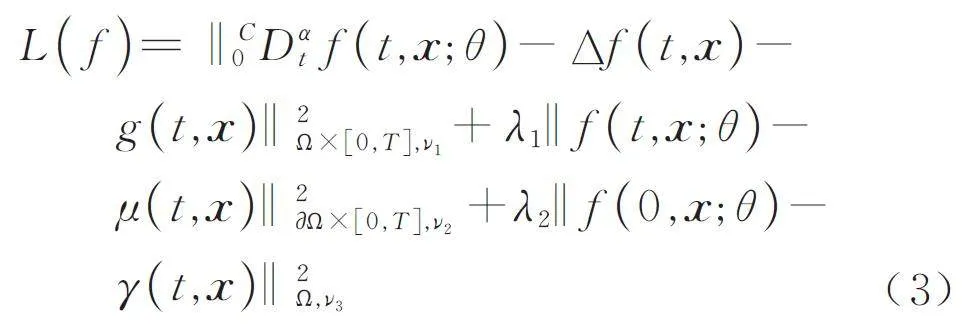
摘 要： 偏微分方程可以用深度學(xué)習(xí)方法求解，其求解思路是構(gòu)建損失函數(shù)、采集樣本點(diǎn)，然后在采集到的時(shí)空樣本點(diǎn)上利用隨機(jī)梯度下降法訓(xùn)練神經(jīng)網(wǎng)絡(luò)，直接去逼近方程，從而把方程求解問題轉(zhuǎn)化為極小化損失函數(shù)的問題. 特別地，對(duì)時(shí)間分?jǐn)?shù)階擴(kuò)散方程而言，損失函數(shù)刻畫了神經(jīng)網(wǎng)絡(luò)與方程的分?jǐn)?shù)階算子、初值條件、邊界條件等的逼近程度. 常見的損失函數(shù)有均方誤差損失函數(shù)及交叉熵誤差函數(shù). 理論上，使損失函數(shù)減小到零的神經(jīng)網(wǎng)絡(luò)就是方程的解.本文證明，用深度學(xué)習(xí)方法求解時(shí)間分?jǐn)?shù)階擴(kuò)散方程時(shí)均方誤差損失函數(shù)可以減小到零，且相應(yīng)的神經(jīng)網(wǎng)絡(luò)在解區(qū)域上一致收斂到方程的真解，因而此時(shí)的神經(jīng)網(wǎng)絡(luò)就是方程的解. 數(shù)值算例驗(yàn)證了理論分析.

關(guān)鍵詞： 神經(jīng)網(wǎng)絡(luò)； 時(shí)間分?jǐn)?shù)階擴(kuò)散方程； 數(shù)值分析

中圖分類號(hào)： O241. 82 文獻(xiàn)標(biāo)志碼： A DOI： 10. 19907/j. 0490-6756. 2024. 041003

1 引言

反常擴(kuò)散過程可以用時(shí)間分?jǐn)?shù)階擴(kuò)散方程來刻畫. 相比整數(shù)階方程，分?jǐn)?shù)階方程可以描述具有時(shí)間記憶及遺傳性過程的演化，在半導(dǎo)體、信號(hào)處理與電化學(xué)、核磁共振、粘彈性力學(xué)、湍流等諸多領(lǐng)域有著廣泛的應(yīng)用［1-11］. 含時(shí)間分?jǐn)?shù)階導(dǎo)數(shù)的擴(kuò)散方程稱為時(shí)間分?jǐn)?shù)階擴(kuò)散方程，一般形式為

C0 Dαtu （ t，x ）= Δu （ t，x ）+ g （ t，x ），

其中x = （ x1，x2，…，xd ），d 為空間維度. 當(dāng)α ∈ （ 0，1 ） 時(shí)，方程稱為時(shí)間分?jǐn)?shù)階慢擴(kuò)散方程；當(dāng)α ∈ （ 1，2 ） 時(shí)，方程稱為時(shí)間分?jǐn)?shù)階超擴(kuò)散方程；當(dāng)α = 1 時(shí)，方程退化為經(jīng)典擴(kuò)散方程. 近年來，時(shí)間分?jǐn)?shù)階擴(kuò)散方程的數(shù)值解法廣受關(guān)注，主流的數(shù)值方法包括有限差分法，有限元法及譜方法，等［2］.但是，由于分?jǐn)?shù)階導(dǎo)數(shù)的非局部性，方程的數(shù)值計(jì)算需要大量運(yùn)算及存儲(chǔ).

深度學(xué)習(xí)方法也可以求解微分方程. 由萬能逼近定理，在非常一般的假設(shè)下，只要隱藏層中隱藏單元的數(shù)量足夠多，標(biāo)準(zhǔn)前饋神經(jīng)網(wǎng)絡(luò)就可以近似任何連續(xù)或不連續(xù)函數(shù). 與數(shù)值方法不同，深度學(xué)習(xí)方法不需要剖分網(wǎng)格，而是通過構(gòu)建損失函數(shù)來刻畫神經(jīng)網(wǎng)絡(luò)解與微分方程的微分算子和初邊值條件等的逼近程度，并在時(shí)間和空間域中樣本點(diǎn)上利用隨機(jī)梯度下降法訓(xùn)練神經(jīng)網(wǎng)絡(luò)，通過極小化損失函數(shù)來直接逼近方程. 該方法適用于解那些計(jì)算量較大的方程. 理論上，用神經(jīng)網(wǎng)絡(luò)求解微分方程時(shí)所構(gòu)建的損失函數(shù)越接近于零代表該神經(jīng)網(wǎng)絡(luò)越接近于方程的真解，使損失函數(shù)等于零的神經(jīng)網(wǎng)絡(luò)解就可以被視為方程的真解.

與數(shù)值方法相比，雖然深度學(xué)習(xí)方法求解微分方程高效便捷，但當(dāng)前卻缺少完善的理論支撐，可靠性有待論證. 因此，研究深度學(xué)習(xí)方法的計(jì)算理論具有重要的理論和應(yīng)用價(jià)值. 在本文中，我們證明：用深度學(xué)習(xí)方法求解時(shí)間分?jǐn)?shù)階擴(kuò)散方程時(shí)所構(gòu)建的均方誤差形式的損失函數(shù)可以減小至零，且相應(yīng)的神經(jīng)網(wǎng)絡(luò)解一致收斂于方程的真解，即神經(jīng)網(wǎng)絡(luò)解就是方程的真解.

后文的結(jié)構(gòu)如下. 第2 節(jié)介紹深度學(xué)習(xí)方法求解分?jǐn)?shù)階擴(kuò)散方程的思路. 第3 節(jié)證明，若構(gòu)建一個(gè)滿足一定條件的神經(jīng)網(wǎng)絡(luò)函數(shù)集那么在集合中一定存在一個(gè)神經(jīng)網(wǎng)絡(luò)函數(shù)，使得損失函數(shù)減小到零且一致收斂于方程的真解. 第4 節(jié)用算例驗(yàn)證了深度學(xué)習(xí)方法求解時(shí)間分?jǐn)?shù)階擴(kuò)散方程的效能. 第5 節(jié)總結(jié)研究所得結(jié)果.

2 深度學(xué)習(xí)方法

考慮如下形式的d 維時(shí)間分?jǐn)?shù)階擴(kuò)散方程：

其中x = （ x1，x2，…，xd ），d 為空間維度，Ω 為對(duì)應(yīng)的d 維空間區(qū)域，g，γ，μ 分別為Ω × [ 0，T ]，Ω，?Ω ×[ 0，T ] 上給定的連續(xù)函數(shù)，滿足μ （ 0，x ）|x ∈ ?Ω =r （ x ），Δ 為L(zhǎng)aplace 算子， C0 Dαtu （ t，x ） 為左Caputo分?jǐn)?shù)階導(dǎo)數(shù)，定義如下：

定義2. 1（左Caputo 分?jǐn)?shù)階導(dǎo)數(shù)） 如果α ∈ R是正數(shù)且n - 1 ≤ α ≤ n，n ∈ N+，f （ t ） 是定義在[ 0，T ] 上的連續(xù)函數(shù)，定義α 階左Caputo 分?jǐn)?shù)階導(dǎo)數(shù)為

其中t ∈ [ 0，T ]，n =[ α ]+ 1，Γ（ ? ）是Gamma 函數(shù).

利用深度學(xué)習(xí)方法求解方程（1）的具體思路如下. 構(gòu)建損失函數(shù)，將尋找偏微分方程數(shù)值解的問題轉(zhuǎn)化為極小化損失函數(shù)的優(yōu)化問題，其中的損失函數(shù)用于衡量神經(jīng)網(wǎng)絡(luò)解對(duì)方程的分?jǐn)?shù)階微分算子、初值條件、邊界條件等的逼近程度. 然后，通過在時(shí)間和空間區(qū)域上采集樣本點(diǎn)，將采集到的樣本點(diǎn)代入損失函數(shù)，利用隨機(jī)梯度下降法訓(xùn)練神經(jīng)網(wǎng)絡(luò)，使損失函數(shù)下降為零，直接逼近偏微分方程. 理論上，使損失函數(shù)減小到零的那組神經(jīng)網(wǎng)絡(luò)就是我們要尋找的神經(jīng)網(wǎng)絡(luò)解.

損失函數(shù)一般可用均方誤差的形式來定義，即

其中f （t，x；θ） 為神經(jīng)網(wǎng)絡(luò)函數(shù)，θ 為神經(jīng)網(wǎng)絡(luò)的參數(shù)，‖f （ y）‖2Y，ν = ∫Y|f （ y ）|2 ν （ y ） dy，ν （ y ） 是Y 上y的正概率密度，λ1，λ2 為懲罰項(xiàng). L （ f ） 是需要極小化的損失函數(shù)，它衡量了神經(jīng)網(wǎng)絡(luò)解和方程的真解之間的接近程度，L （ f ） 越接近于0 代表神經(jīng)網(wǎng)絡(luò)解f （t，x；θ） 越接近方程的真實(shí)解. 如果L （ f ） = 0，那么神經(jīng)網(wǎng)絡(luò)函數(shù)f （t，x；θ） 就可以被視為方程的解. 這樣，求解方程的問題就轉(zhuǎn)化為如何極小化損失函數(shù)L （ f ） 的優(yōu)化問題，而極小化損失函數(shù)的這組神經(jīng)網(wǎng)絡(luò)就是方程的一個(gè)神經(jīng)網(wǎng)絡(luò)解.

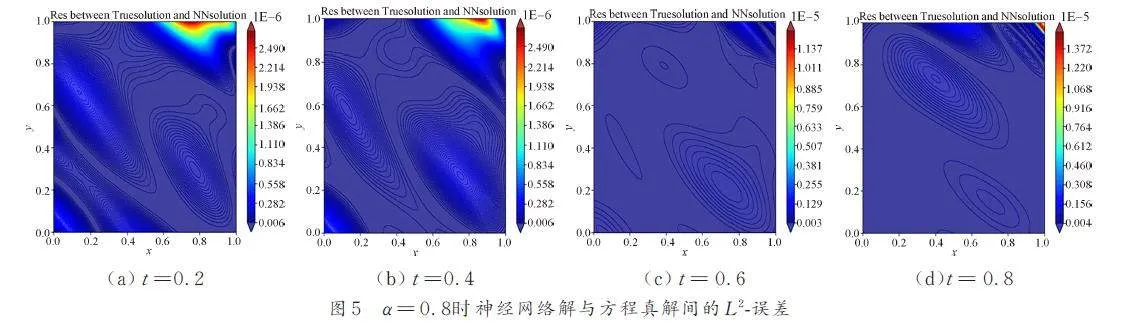
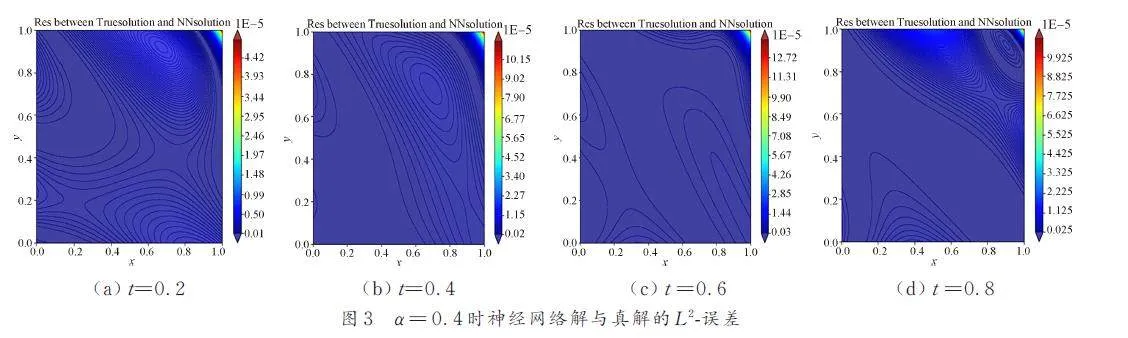
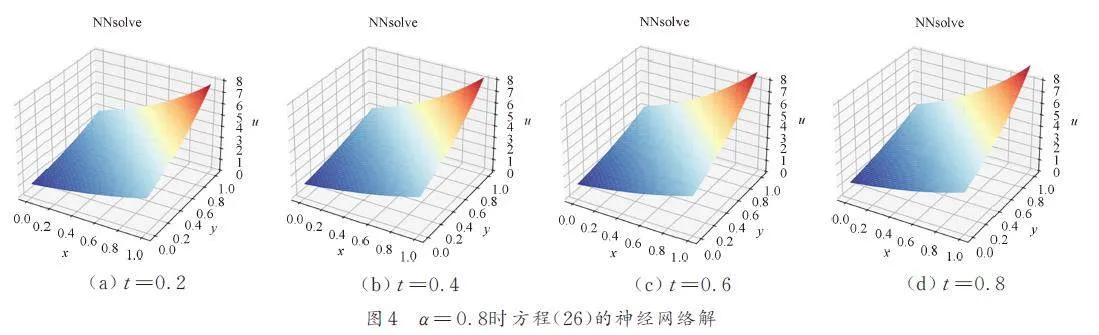
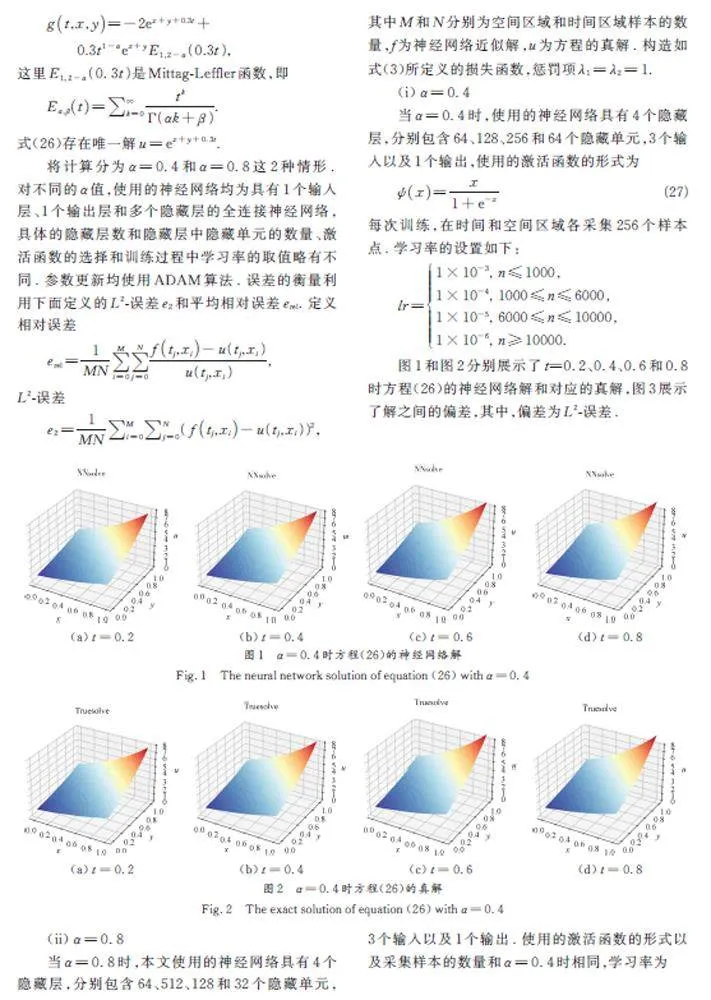
圖4 展示了t = 0. 2， 0. 4，0. 6和0. 8 時(shí)方程（26）的神經(jīng)網(wǎng)絡(luò)解，對(duì)應(yīng)的真解如圖2 所示. 圖5展示了解之間的偏差，這里的偏差為L(zhǎng)2-誤差.

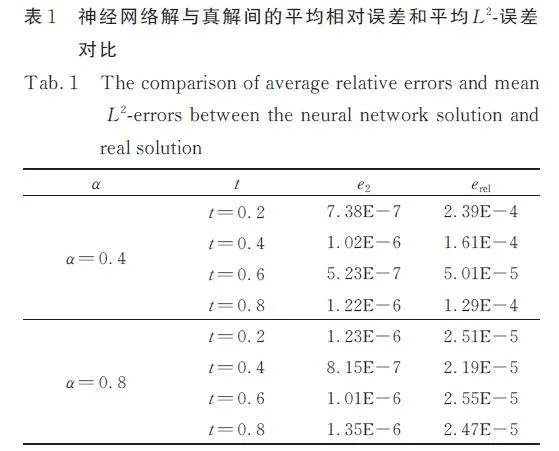
表1 為2 種不同分?jǐn)?shù)階取值下用深度學(xué)習(xí)求解方程（26）得到的方程的真解和神經(jīng)網(wǎng)絡(luò)間的誤差，誤差在整個(gè)時(shí)間區(qū)域上的動(dòng)態(tài)變化如圖6 所示，其中的紅色線為平均相對(duì)誤差erel，藍(lán)色線為平均L2-誤差e2.

綜上，數(shù)值計(jì)算的結(jié)果表明，神經(jīng)網(wǎng)絡(luò)解與真解間的誤差非常小，與本文的理論分析一致，說明深度學(xué)習(xí)方法確實(shí)可以有效求解時(shí)間分?jǐn)?shù)階擴(kuò)散方程.

5 結(jié)論

本文研究了用深度學(xué)習(xí)方法求解分?jǐn)?shù)階偏微分方程的數(shù)學(xué)理論，證明當(dāng)隱藏層中隱藏單元的數(shù)量足夠多時(shí)，配備了有界非常數(shù)激活函數(shù)的神經(jīng)網(wǎng)絡(luò)即便僅有1 個(gè)隱藏層，其均方誤差損失函數(shù)也可以減小到0，并且使損失函數(shù)減小到0 的神經(jīng)網(wǎng)絡(luò)解在解區(qū)域上一致收斂到方程的真解. 數(shù)值算例驗(yàn)證了理論分析.

參考文獻(xiàn)：

［1］ Oldham K B， Spanier J. The fractional calculus［ M］.London： Academic Press， 1974.

［2］ Podlubny I. Fractional differential equations ［M］.San Diego： Academic Press， 1999.

［3］ Hornik K. Approximation capabilities of multilayerfeedforward networks ［J］. Neural Networks， 1991，4： 251.

［4］ Li X， Xu C. Existence and uniqueness of the weaksolution of the space-time fractional diffusion equationand a spectral method approximation ［J］. CommunComput Phys， 2010， 8： 1016.

［5］ Luchko Y. Initial-boundary-value problems for theone-dimensional time-fractional diffusion equation［ J］.Fract Cal Appl Anal， 2012， 15： 141.

［6］ Stynes M， Riordan E， Gracia， et al. Error analysisof a finite difference method on graded meshes for atime-fractional diffusion equation ［J］. SIAM J NumerAnal， 2017， 55： 1057.

［7］ Gorenflo R， Luchko Y， Yamamoto M. Timefractionaldiffusion equation in the fractional Sobolevspaces［ J］. Fract Cal Appl Anal， 2015， 18： 799.

［8］ Sakamoto K， Yamamoto M. Initial value/boundaryvalue problems for fractional diffusion-wave equationsand applications to some inverse problems ［J］.J Math Anal Appl， 2011， 382： 426.

［9］ Boccardo L， Dallaglio A. Nonlinear parabolic equationswith measure data ［J］. J Funct Anal， 1997，147： 237.

［10］ Sirignano J， Spiliopoulos K. DGM： A deep learningalgorithm for solving partial differential equations［ J］.J Comput Phys， 2018， 375： 1339.

［11］ Chen W， Sun H G. Numerical algorithms for fractionaldifferential equations： Current situation andproblems ［J］. Computer-Aided Engineering， 2010，19： 1.［陳文， 孫洪廣. 分?jǐn)?shù)階微分方程的數(shù)值算法： 現(xiàn)狀和問題［J］. 計(jì)算機(jī)輔助工程， 2010，19： 1.］

（責(zé)任編輯： 周興旺）

基金項(xiàng)目： 國(guó)家自然科學(xué)基金（11971337）