考慮中心距安裝誤差下的齒面磨損特性分析

摘"要：以重合度為1～2之間的定軸漸開線直齒輪為研究對象，基于Archard磨損模型數值仿真齒面磨損的分布規律，研究齒輪中心距安裝誤差對齒輪嚙合過程的影響，揭示中心距安裝誤差對齒面磨損的影響機理。結果表明：在0.1%的中心距誤差下，中心距的增大會使齒輪的重合度下降，嚙合區域變小，嚙入點的位置遠離齒根，從而減小齒面磨損。

關鍵詞：齒面磨損；特性分析；Archard磨損模型；中心距；安裝誤差

中圖分類號：TH117.1""文獻標志碼：A""文章編號：1671-5276（2024）02-0015-05

Analysis of Tooth Face Wear Characteristics under Center Distances Installation Error

SUN Bin， WANG Youren， GAO Jiahao

（College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

Abstract：Taking fixed-axle involute spur gears with coincidence degree between 1～2 as the research objects， the distribution law of tooth surface wear was simulated numerically based on Archard wear model， the influence of gear center distance on gear meshing process was studied， and the influence mechanism of center distance on tooth surface wear was revealed. The results show that with 0.1% of the center distance error， the increase of the center distance will reduce the gear overlap， make the meshing area smaller and keep the rod position far away from the root， thus reducing the wear on the tooth surface.

Keywords：wear of tooth surface; characteristic analysis; Archard wear model; gear center distance; installation error

0"引言

作為機械傳動方式中重要的基礎元件之一，齒輪具有傳動效率高、傳動比準確、工作可靠等優點，被廣泛應用于航空航天、汽車、船舶、工程機械等諸多領域。對于齒輪機構來說，過度的齒面磨損會使齒輪齒廓發生變化，不但齒輪傳動比的精確度和傳動效率會受到影響，而且還可能會造成強烈的沖擊使齒輪斷裂、機構損壞等。因此，有必要研究齒輪磨損的動態過程，從而盡可能小地減少損失。潘冬等［1］利用Archard磨損模型，考慮了齒輪負載及轉速的影響，對齒輪磨損問題進行了數值仿真。石萬凱等［2］研究了齒面表面粗糙度對齒面磨損的影響。張俊等［3］建立了準靜態工況下的齒面磨損模型，并分析了負載和嚙合偏差對齒面磨損的影響。朱麗莎等［4］考慮了齒間動態載荷分配對齒面磨損的影響。張建閣等［5］研究了一種潤滑油齒輪磨損分析模型。王曉筍等［6］研究了齒間動態嚙合力下齒輪的動態磨損特性。周江建等［7］研究了齒輪磨損對其振動信號特征的影響。由此可見，大多數學者對于齒面磨損問題的研究均以“負載”、“轉速”為影響變量探究齒輪的磨損規律，對于齒輪副中心距對齒面磨損的影響卻少有提及。事實上，齒輪以不同中心距安裝時，會使齒輪副的接觸情況產生變化，從而對齒面磨損深度產生影響。

本文基于Archard磨損模型，利用數值分析的方法，研究了漸開線齒輪齒面磨損規律，分析了齒輪中心距對齒輪嚙合過程的影響，揭示了中心距對齒面磨損的影響機理。

1"齒輪嚙合過程

以重合度為1～2之間的定軸漸開線直齒輪為研究對象，設其模數為m，分度圓壓力角為α，主、從動輪的齒數分別為z1、z2，嚙合過程如圖1所示。圖中O1、O2分別為主、從動輪的基圓圓心；rb1、rb2分別為主、從動輪的基圓半徑；ra1、ra2分別為主、從動輪的齒頂圓半徑；pb為基圓齒距；設N1N2為兩齒輪基圓的公切線，N1、N2為切點，則N1N2為理論嚙合線；設B1為從動輪齒頂圓與N1N2的交點，B2為主動輪齒頂圓與N1N2的交點，則B1B2為實際嚙合線，其中B1為嚙入點，B2為嚙出點，B1C1、C2B2為雙齒嚙合區，C1C2為單齒嚙合區；設O1O2與N1N2的交點為P，則P為節點；線段O1O2的長度即為齒輪副的中心距A。

根據齒輪嚙合原理，齒輪副標準中心距A的計算公式為

A=（z1+z2）m2（1）

實際中心距與標準中心距之間的關系為

A′cosα′=Acosα（2）

式中：A′為實際中心距；α′為節點壓力角。

2""齒輪副磨損模型

2.1"齒面接觸應力

采用集中質量法建立主、從動齒輪動力學方程，設me為等效質量；x為嚙合線上兩齒輪相對位移；e（t）為齒輪的綜合誤差；T為負載轉矩；θ1和θ2分別為主、從動齒輪的扭轉角位移；J1和 J2分別為主、從動齒輪轉動慣量；Mm表示時變嚙合剛度；M-m表示時變嚙合剛度的平均值。則典型的一對齒輪副扭轉振動模型可以表示為［8］

mex··+cmx·+Mmf（x）=Trb2－mee··（t）

x=rb1θ1-rb2θ2-e（t）

me=J1J2J1r2b1+J2r2b2

cm=2ξM-mme（3）

式中：ξ為輪齒嚙合阻尼比；f（x）是與齒側間隙有關的非線性函數。

用Δn表示齒側間隙，則f（x）可以表示為

f（x）=x0x+Δn"xgt;0

－2Δn＜x≤0

x≤－2Δn（4）

輪齒間的動態嚙合力Fn可以表示為

Fn=cmx·+Mmf（x）（5）

對于重合度為1～2之間的齒輪，由于齒輪不斷地處于單齒嚙合區和雙齒嚙合區的交替運動中，其單位齒寬載荷也隨嚙合點位置的不同而不同，因此需要進行載荷分配。定義Δ為由磨損造成的兩齒輪間的幾何側隙，當嚙合點的位置在圖1中的B1C1段時

|Δ|=|hw1（y）+hw2（y）－［hw1（y+pb）+hw2（y+pb）］| （6）

當嚙合點的位置在圖1中的C2B2段時

|Δ|=|hw1（y）+hw2（y）－［hw1（y－pb）+hw2（y－pb）］| （7）

式中：hw1和hw2分別為主、從動輪的磨損量；y為嚙合點到節點的距離；pb為基圓齒距。

設齒輪齒寬為B，齒面單位法向載荷為W，則有：

當Δ＜0時

W=M1（Fn+|Δ|M2）（M1+M2）Bcosα′（8）

當Δgt;0時

W=M1（Fn－|Δ|M2）（M1+M2）Bcosα′（9）

式中M1和M2分別為參與嚙合的兩對齒輪的時變嚙合剛度。

設齒輪副等效彈性模量為Ez，接觸點等效曲率半徑為Rz，赫茲接觸半寬為b，平均接觸應力為σ，它們的計算公式如下：

1Ez=1－δ21E1+1－δ22E2（10）

1Rz=1R1+1R2（11）

b=4WEzπRz（12）

σ=W2b（13）

式中：δ1、δ2分別為主、從動輪材料的泊松比；E1、E2分別為主、從動輪材料的彈性模量；R1=rb1tanαk、R2=rb2tanαk分別為主、從動輪的曲率半徑；αk為嚙合點處的壓力角。

2.2"滑動距離

齒輪回轉任意角度時，定義主、從動輪齒面對應嚙合點之間的相對距離稱為滑動距離。在某一嚙合位置，設主動輪切向速度為v1、滑動距離為L1，從動輪切向速度為v2、滑動距離為L2，它們的計算方式為：

v1=ω1R1（14）

v2=ω2R2（15）

L1=2b1－v2/v1（16）

L2=2b1－v1/v2（17）

式中ω1、ω2分別為主動輪和從動輪的角速度。

2.3"磨損系數

磨損系數的計算對于磨損模型的準確度有著重要的影響。許多學者在研究磨損規律時，一般取經驗值作為磨損系數的值。JANAKIRAMAN V等［9］ 對嚙合過程中的載荷、速度、潤滑特性等因素對磨損系數的影響進行了實驗，利用回歸分析的方法得到了靜態磨損系數的計算公式

k0=3.981×1029EzF1.219LG－7.377S1.589（18）

式中：FL、G、S分別為與載荷、潤滑油壓力黏度系數和復合粗糙度有關的系數，它們的計算方式為：

FL=WEzRzG=y0EzS=RaRz（19）

式中：y0為潤滑油壓力黏度系數；Ra為齒面粗糙度方均根值。

考慮油膜厚度的影響，PRIEST M等［10］提出了一種近似的動態磨損系數模型：

k=k02k0（4－λ）/70"λ＜0.50.5≤λ≤4λgt;4（20）

式中λ為膜厚比系數，其計算公式為

λ=hminRa21+Ra22（21）

式中：Ra1、Ra2分別為主、從動輪的表面粗糙度；hmin為輪齒間最小油膜厚度［11］，計算公式為

hmin=1.6y0.60（vfvu）0.7E0.03zR0.43zW－0.13（22）

式中：vu=（v1+v2）/2為卷吸速度；vf為潤滑油的動力黏度。

根據式（21）—式（22）得到膜厚比系數的范圍，然后由式（18）—式（19）計算出靜態磨損系數，將其代入式（20）中，即可得到較為合理的動態磨損系數。

2.4"齒面磨損模型

目前應用最廣泛的磨損計算公式是Archard磨損模型［12］，其表達式為

WL=KFH（23）

式中：W為磨損體積；L為滑動距離；K為無量綱磨損系數；F為法向接觸力；H為材料硬度。

由于齒輪運轉過程中接觸點是不斷變化的，在實際的計算過程中往往需要將式（23）進行離散化，經過N次磨損循環后，嚙合點的線磨損量hw，N為

hw，N=hw，N－1+kN－1σN－1LN－1（24）

式中：kN－1為N－1次磨損循環時的動態磨損系數；σN－1為N－1次磨損循環時的平均接觸應力；LN－1為N－1次磨損循環時的滑動距離。

輪齒經過N次磨損循環后，曲率半徑將發生改變，其曲率半徑將變為

RN=RN－1－hw，N-1（25）

由式（24）可知，齒面磨損與齒面接觸條件息息相關。根據式（2）可知，中心距的改變會導致節點壓力角發生變化，從而對齒輪嚙合過程產生影響，導致齒面接觸條件發生改變，最終影響齒面磨損量。

3"數值分析與討論

3.1"算例參數

以一對定軸漸開線直齒輪為例進行數值計算，齒輪副幾何參數如表1所示。

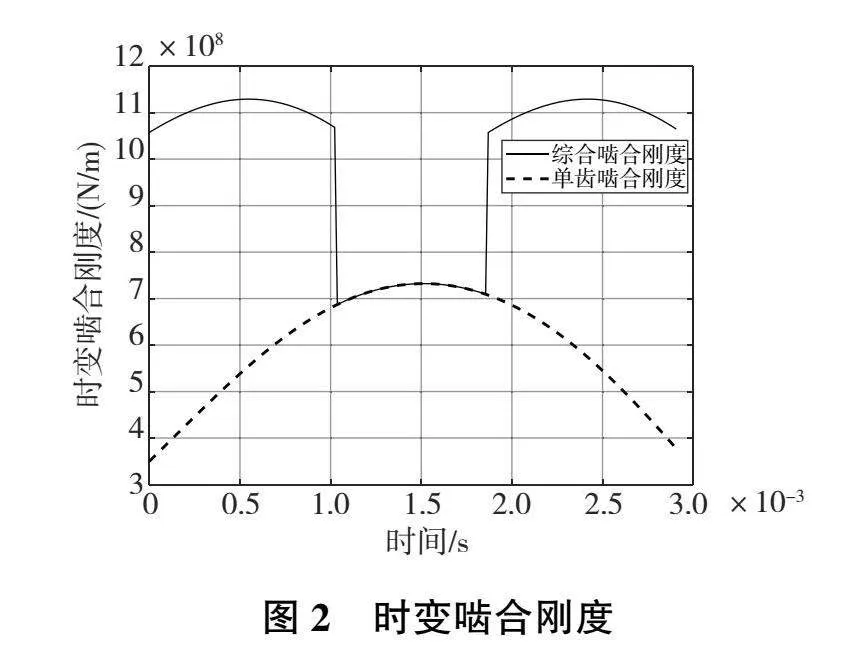
由前文所述，為得到齒輪的磨損量，需要計算輪齒間動態嚙合力并進行載荷分配，因此首先要根據文獻［13］計算考慮非均勻磨損的齒輪時變嚙合剛度，結果如圖2所示。

3.2"中心距誤差對齒面磨損的影響

1）中心距誤差對齒面接觸的影響

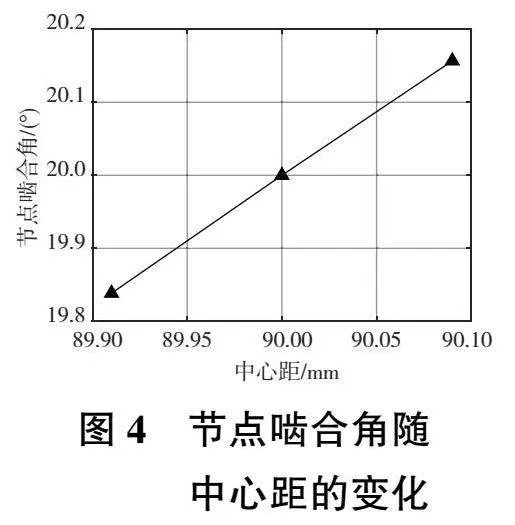
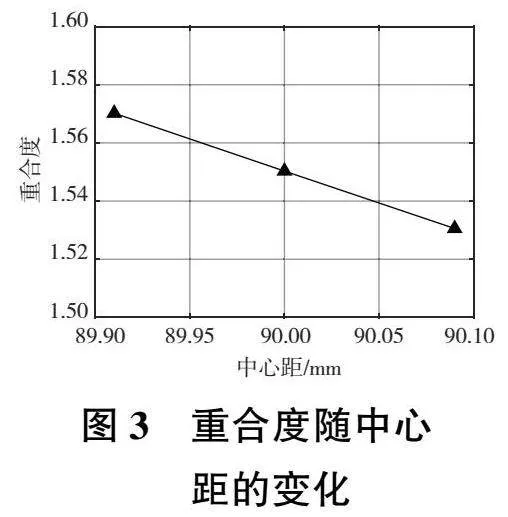
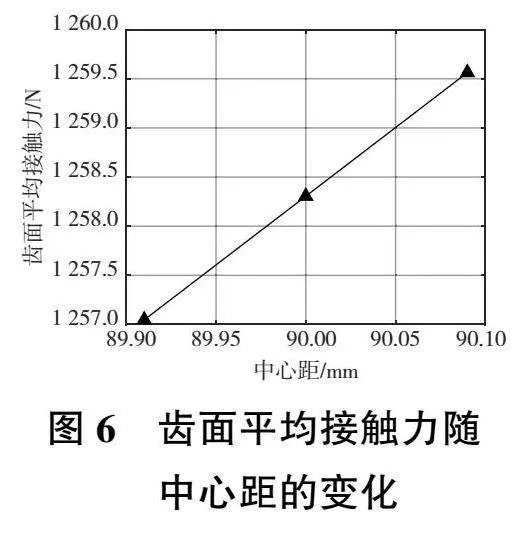
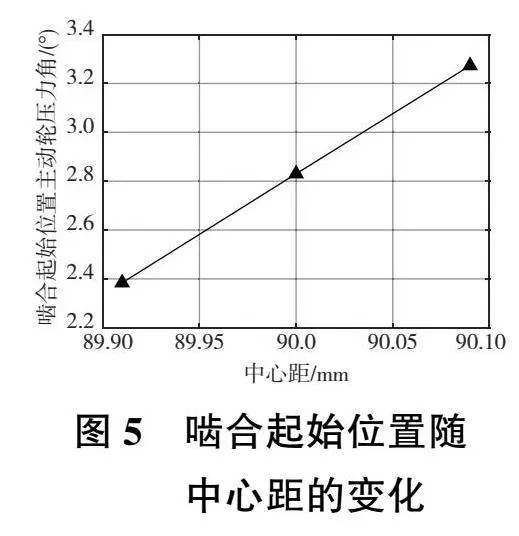
圖3—圖6展示了中心距對齒面接觸的影響。根據齒輪的嚙合原理，中心距誤差雖然不會對齒輪的傳動比產生影響，但是對齒輪的重合度、節點位置、嚙入點位置和齒面平均接觸力均會產生影響。由圖3、圖5可以看出，齒輪對的中心距越小，齒輪對的重合度就越大，且嚙入點越靠近主動輪齒根位置。從圖4中可以看出，當齒輪對為非標準中心距安裝時，節點嚙合角將不再與分度圓壓力角相等。齒輪對的中心距越小，則節點處的嚙合角越小。從圖6中可以看出，隨著中心距的增大，齒面平均接觸力也跟著增大。這是由于隨著齒輪副中心距變大，齒輪節點處的嚙合角增大，從而齒輪所受的圓周力沿齒面法向的分量增加，最終導致了齒面平均接觸力的增大。

2）中心距誤差對齒面磨損的影響

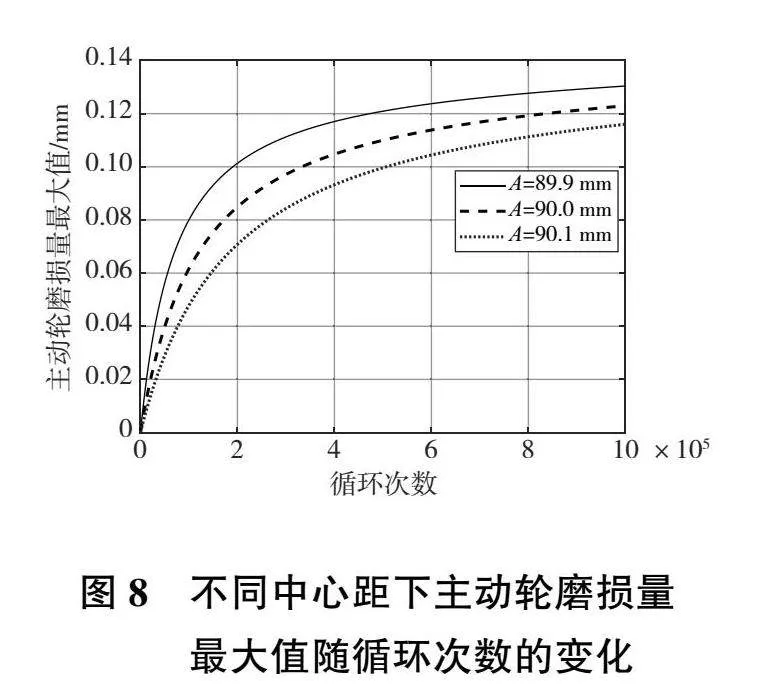
對于表1中的齒輪，分別將中心距增大0.1%和減小0.1%，進行1×106次磨損循環，以主動輪為例，研究不同的中心距對齒面磨損的影響。

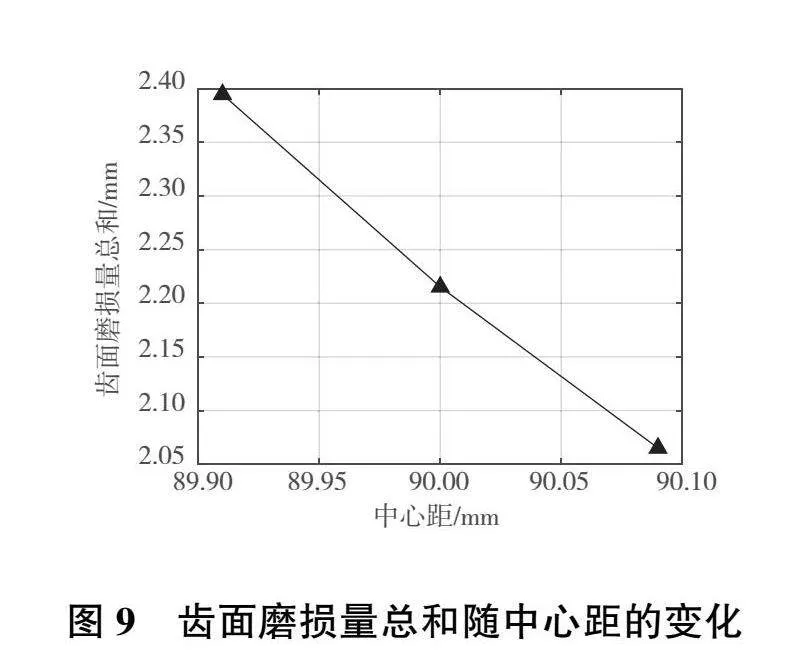
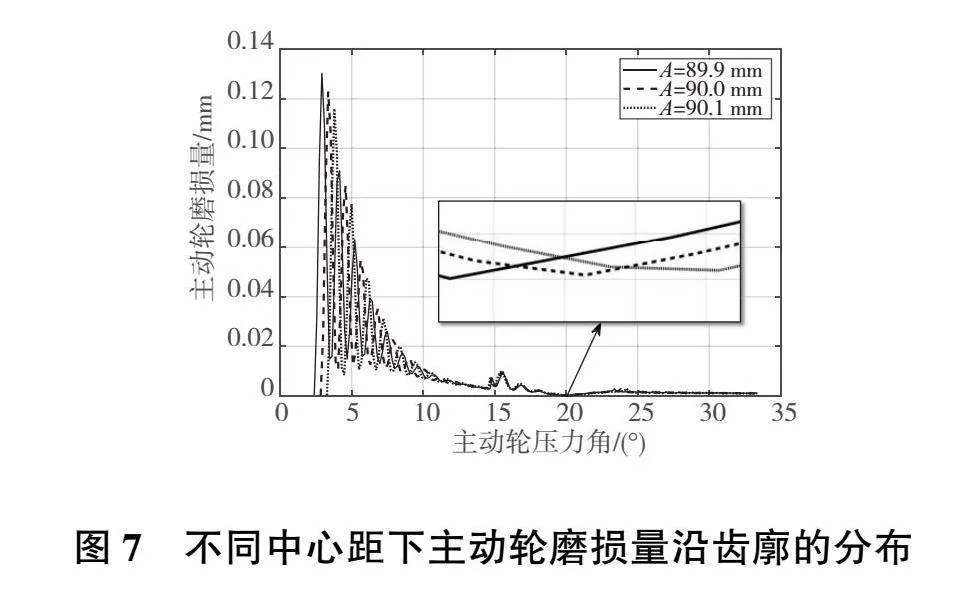
圖7—圖9展示了中心距對齒面磨損量的影響。根據前文的分析，隨著齒輪副中心距增大，齒輪重合度減小，嚙入點位置逐漸遠離齒根。因此，從圖7中可以看出，隨著齒輪副中心距增大，主動輪磨損的區域逐漸減小，開始磨損的位置漸漸遠離齒根。由于齒輪副為非標準中心距安裝時，節點嚙合角不再等于分度圓壓力角，因此主動輪磨損量的最小位置不再是分度圓處，而是在分度圓附近：若實際中心距小于標準中心距，則主動輪磨損量最小位置在分度圓附近靠近主動輪齒根的一邊；若實際中心距大于標準中心距，則主動輪磨損量最小位置在分度圓附近靠近主動輪齒頂的一邊。

從圖8和圖9中可以看出，隨著齒輪副中心距增大，主動輪磨損量的最大值和主動輪齒面磨損量總和均有所減小。根據前文分析，齒輪副中心距增大會導致齒面平均接觸力有所增大，但在中心距誤差只有0.1%的情況下，其增量并不大。由于主動輪磨損量的最大值出現在齒根附近，越靠近齒根主動輪的磨損量越大，而中心距的增大會使嚙入點遠離齒根并減小齒輪磨損區域。因此，隨著齒輪副中心距增大，主動輪磨損量的最大值和主動輪齒面磨損量總和均有所減小。

4"結語

本文以定軸漸開線直齒輪為研究對象，通過數值分析研究漸開線直齒輪的磨損分布規律，分析了中心距誤差對齒輪嚙合過程的影響，揭示了中心距誤差對齒面磨損的影響機理。結果表明：在0.1%的中心距誤差下，中心距的增大會使齒輪的重合度下降，嚙合區域變小；嚙入點的位置遠離齒根，從而減小齒面磨損。

參考文獻：

［1］ 潘冬，趙陽，李娜，等. 齒輪磨損壽命預測方法［J］. 哈爾濱工業大學學報，2012，44（9）：29-33，39.

［2］ 石萬凱，王旭，韓振華，等. 漸開線微齒輪磨損仿真分析［J］. 機械傳動，2016，40（4）：10-14.

［3］ 張俊，卞世元，魯慶，等. 準靜態工況下漸開線直齒輪齒面磨損建模與分析［J］. 機械工程學報，2017，53（5）：136-145.

［4］ 朱麗莎，向磊，鄒常青. 齒間動態載荷分配下的齒輪磨損分析［J］. 西安交通大學學報，2018，52（5）：75-80.

［5］ 張建閣，劉少軍，方特. 混合潤滑下齒面磨損預測研究及試驗驗證［J］. 華南理工大學學報（自然科學版），2018，46（2）：22-30.

［6］ 王曉筍，巫世晶，陳杰，等. 考慮動載荷與動態磨損系數的直齒輪傳動系統動態磨損特性［J］. 中南大學學報（自然科學版），2014，45（2）：408-413.

［7］ 周江建，劉宇晨. 煙草車間傳送設備齒輪磨損智能預警方法研究［J］. 機械制造與自動化，2022，51（3）：244-247.

［8］ HE Z，HU Y M，ZHENG X Y，et al. A calculation method for tooth wear depth based on the finite element method that considers the dynamic mesh force［J］. Machines，2022，10（2）：69.

［9］ JANAKIRAMAN V，LI S，KAHRAMAN A. An investigation of the impacts of contact parameters on wear coefficient［J］. Journal of Tribology，2014，136（3）：031602.

［10］ PRIEST M，TAYLOR C M. Automobile engine tribology—approaching the surface［J］. Wear，2000，241（2）：193-203.

［11］ DOWSON D，HIGGINSON G R. Elasto-hydrodynamic lubrication［M］. SI ed. Oxford England：Pergamon Press，1977.

［12］ ARCHARD J F. Contact and rubbing of flat surfaces［J］. Journal of Applied Physics，1953，24（8）：981-988.

［13］ 何澤銀，唐偉迤，林騰蛟，等. 增速齒輪副非均勻磨損時變嚙合剛度研究［J］. 機械傳動，2019，43（12）：1-6.

收稿日期：20221013