基于隨機振動的線束裝配拉力計算方法

摘"要：為了提高飛機線束在機上裝配的可靠性，確保用電設備之間正常的互聯作用，設計一種檢驗線束裝配牢固的拉力計算方法。通過3個正交方向上的隨機振動試驗獲取線束的響應加速度特征，結合線束在振動過程中的受力模型提出一種基于加速度方均根值的拉力計算方法，并利用搭建的線束拉脫力試驗平臺，驗證了該方法的可行性。

關鍵詞：線束裝配；拉力計算；卡箍；隨機振動；加速度方均根

中圖分類號：V24""文獻標志碼：A""文章編號：1671-5276（2024）02-0144-04

Calculation Method of Wire Harness Assembly Tension Based on Random Vibration

PEI Longtao， YAN Jing， LU Shanshan， ZHANG Yixin

（College of Mechanical and Electrical Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Abstract：In order to improve the reliability of aircraft harness assembly and ensure the normal interconnection between electrical equipment， a force calculation method for inspection harness assembly inspection is designed. The response acceleration characteristics of wire harness are obtained through random vibration tests in three orthogonal directions， and in combination with the force model of wire harness in the vibration process， a force calculation method based on the root mean square value of acceleration is proposed， and its feasibility is verified by the constructed wire harness pull off force test platform.

Keywords：cable harness assembly；pulling force calculation；clamp；random vibration；root mean square of acceleration

0"引言

隨著飛機電氣化程度的增強，用電設備之間各項功能的實現與互聯都要通過機上敷設的線束來實現。在經歷過由飛機線束故障引發的航空災害后，美國聯邦航空安全局于2007年首次將電氣線路互聯系統（electrical wiring interconnection system，EWIS）作為一個單獨的部分進行解釋說明。此后民航局在2011年CCAR-25-R4［1］部修訂版中引入了此概念的相關標準和要求，用于對飛機線路互聯系統的解釋和規定。線束作為EWIS的主要組成部分，在機上安裝的可靠性對日常的功能實現有著重要的作用［2］。線束的安裝和固定主要是通過帶墊金屬卡箍上的螺栓連接固定在飛機結構上［3］。目前對于此類帶墊金屬卡箍的研究主要集中在分類和選型上。鄭敏等［4］介紹了常見航空卡箍的分類及使用情況，分析了固定類卡箍的選用原則。王丹等［5］針對航空帶墊金屬卡箍的選用問題，提出了基于構型和材料兩方面的選用建議。

關于此類航空卡箍的分類和選型研究已逐漸成熟，但在線束與卡箍裝配方面的研究較少，特別是對于線束在卡箍內裝配可靠性問題目前沒有一個較好的解決方法。美國國防部MIL-HDBK-522A［6］、MIL-W-50881G［7］以及SAE-AIR6808［8］標準文件中對線束與金屬帶墊卡箍的裝配檢驗要求中提出，線束在卡箍中的裝配可靠性需要通過在線束端施加軸向拉力的方式來檢驗，如線束在一定軸向力下不會從卡箍中滑出，則線束在卡箍內固定合適。線束在卡箍內軸向移動的原因來源于振動。該文件中并沒有給出此軸向力的計算表達式，對于實際線束的檢驗指導仍存在困難。為此，本研究在隨機振動試驗的基礎上，提出了檢驗線束在卡箍內裝配可靠性的方法，給出了軸向力的計算表達式，可為機上線束的裝配檢驗提供參考。

1"線束與卡箍裝配的隨機振動試驗

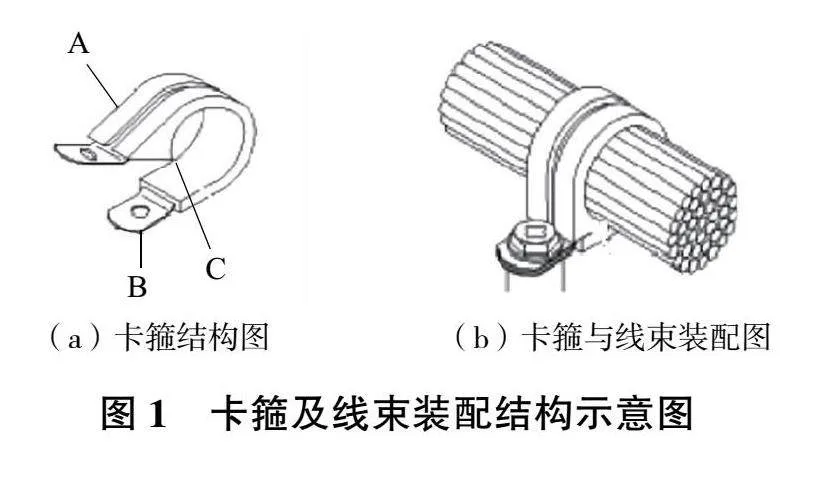
線束裝配所用卡箍結構主要由兩部分組成：橡膠襯墊（A）和金屬箍帶（B），襯墊上的楔形塊（C）使得卡箍內緣呈現圓形，可以提高線束與卡箍的接觸面積，同時防止異物進入卡箍內，如圖1（a）所示。將一定直徑的線束放置在卡箍內，通過螺栓連接使帶有螺栓孔的箍帶耳片貼合，從而實現線束的安裝固定，如圖1（b）所示。

1.1"振動試驗的條件設置

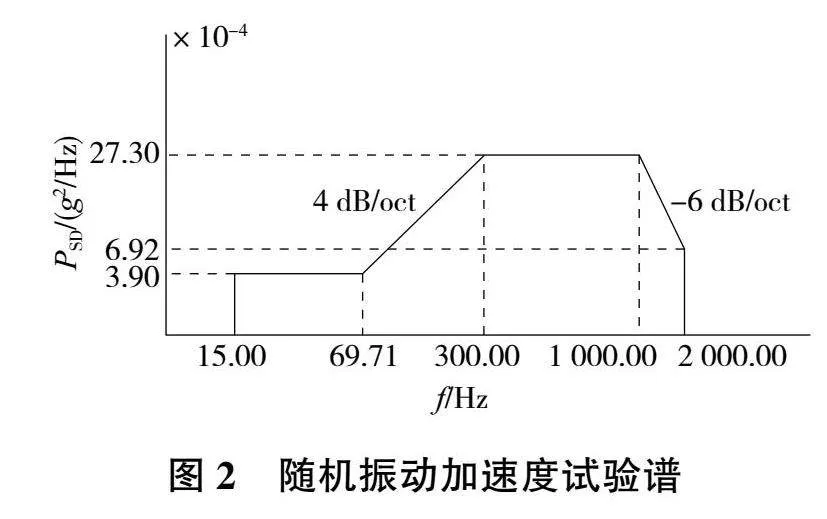
圖2為試驗參考譜，頻帶范圍為15～2 000Hz，加速度方均根值為1.91g。在給定參考譜下，通過三軸向振動臺分別對線束與卡箍的裝配體進行x、y和z 3個方向上的單獨激勵，激勵時長0.5h。圖3為試驗過程圖。

1.2"隨機振動試驗數據的檢驗

隨機信號分為穩態隨機信號和非穩態隨機信號。對穩態隨機信號，統計特性不隨時間發生變化，可以用有限時間長度的樣本來描述整個隨機振動過程；非穩態隨機信號的統計量隨時間發生變化，不能用統計量來量化描述隨機行為。所以在分析振動數據的統計特性前，需要對振動測試中的數據進行檢驗［9］。

1）正態性檢驗

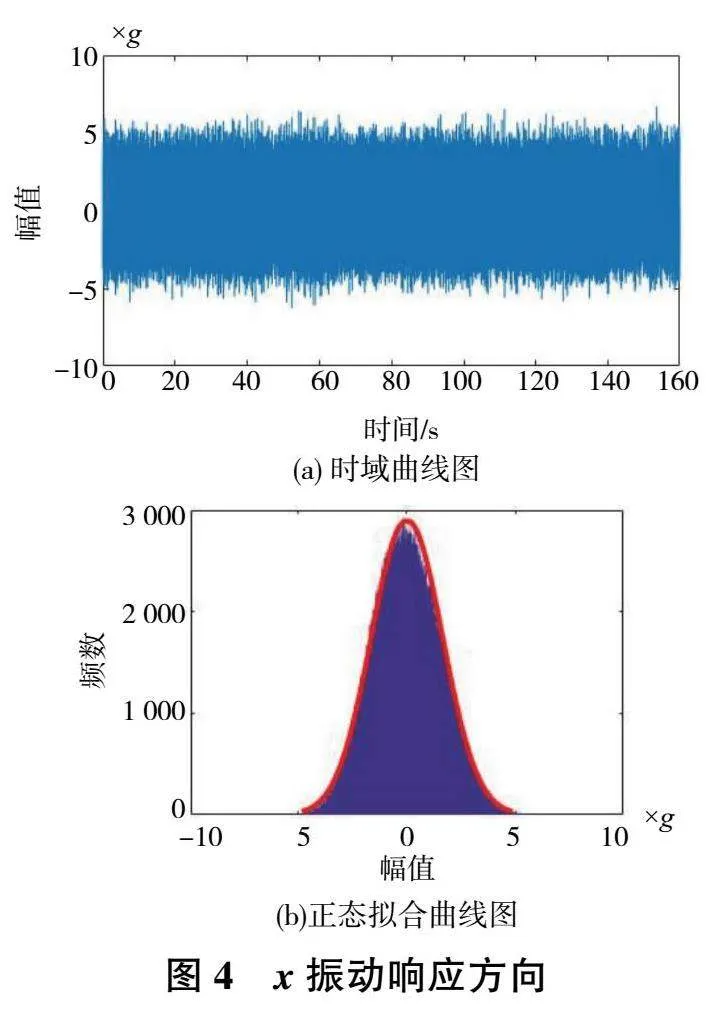
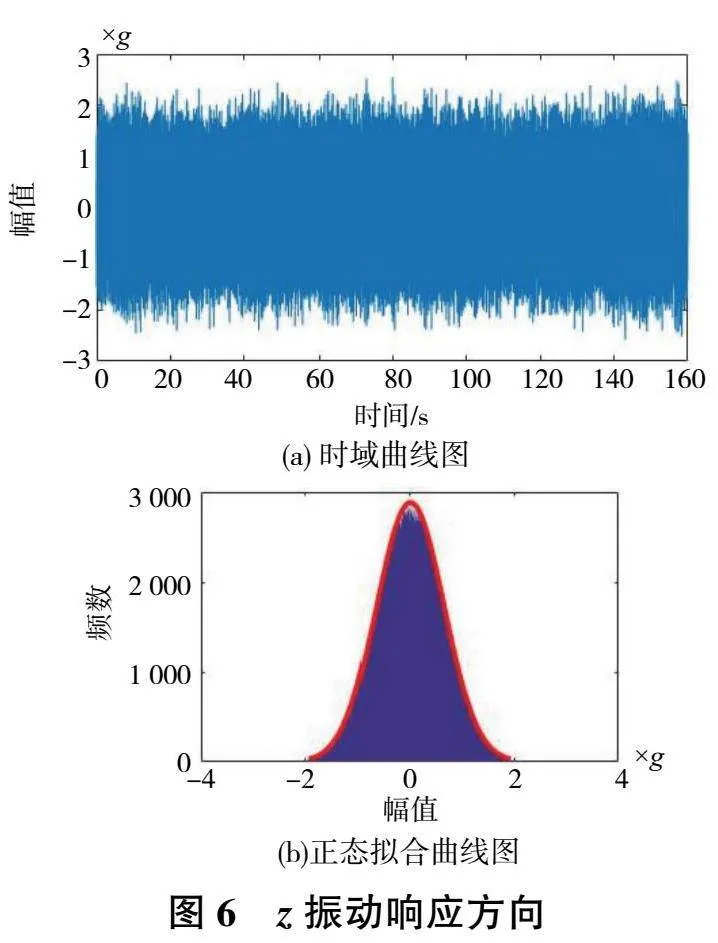
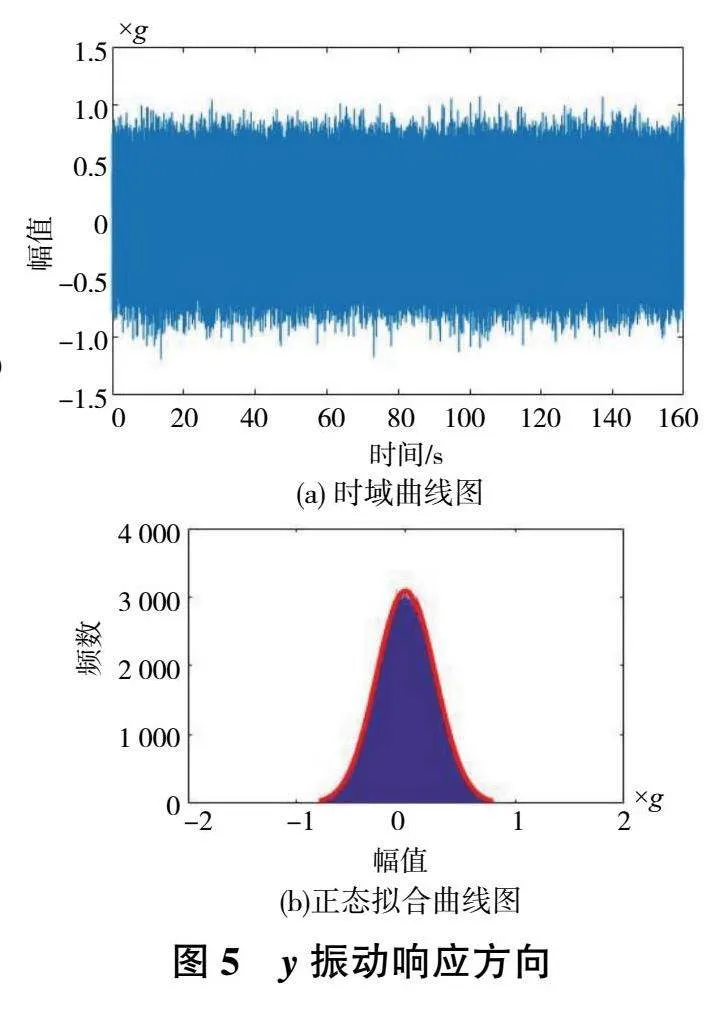
選取振動數據中的一段作為該隨機振動下的樣本，利用直方圖法進行正態分布檢驗，圖4、圖5和圖6分別為x方向、y方向和z方向線束加速度時域曲線圖和正態分布擬合圖。從正態擬合曲線圖中可以看出線束加速度數據服從正態分布。

2）穩態性檢驗

隨機振動的穩態性檢驗方法有目視檢查法、方均根值檢驗法等。

目視檢查法是通過目視的方法觀察振動信號波形的時間歷程，若信號波形波動很小，振動波形的峰谷變化比較均勻，就可近似認為該信號是平穩的。方均根值檢驗法是將振動信號不同時間樣本的方均根值輸至一方均根表，判斷不同時間樣本方均根值隨時間的變化情況，若變化很小，可認為該信號平穩。

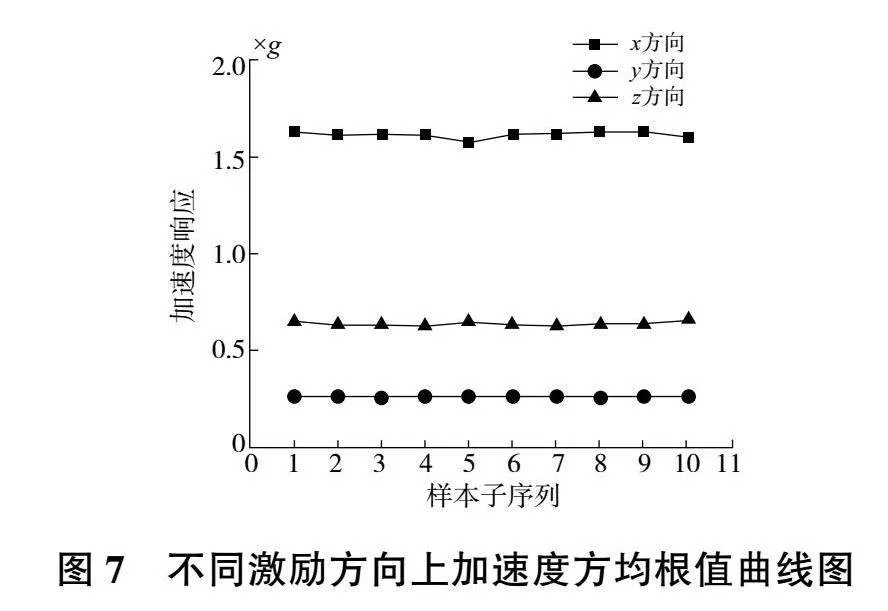
這里選用方均根值檢驗法來檢測隨機信號的穩態性，將3個方向上的樣本時域振動數據分為10段，各段在時間上保持連續，分別對10段數據計算加速度方均根值并作圖，如圖7所示。

根據圖7中各方向上的加速度方均根值變化曲線，可以看出加速度方均根數據變化比較平穩，因此可認為該隨機信號屬于穩態隨機振動信號。

2"振動數據分析

2.1"時域分析

對于一個穩態隨機振動信號，其時域統計特征量可分別由均值、方差、方均值來描述。分別計算3個方向上加速度響應數據的時域統計量，計算結果如表1所示。

由表1中可以看出線束加速度響應屬于均值為0的穩態隨機振動，振動數據的方差值等于方均值。其中x方向方均根值最大， y方向上的方均根值最小。x激勵方向與線束軸向方向相同，線束最容易在卡箍內失效滑動的振動來自于線束軸向方向。

2.2"頻域分析

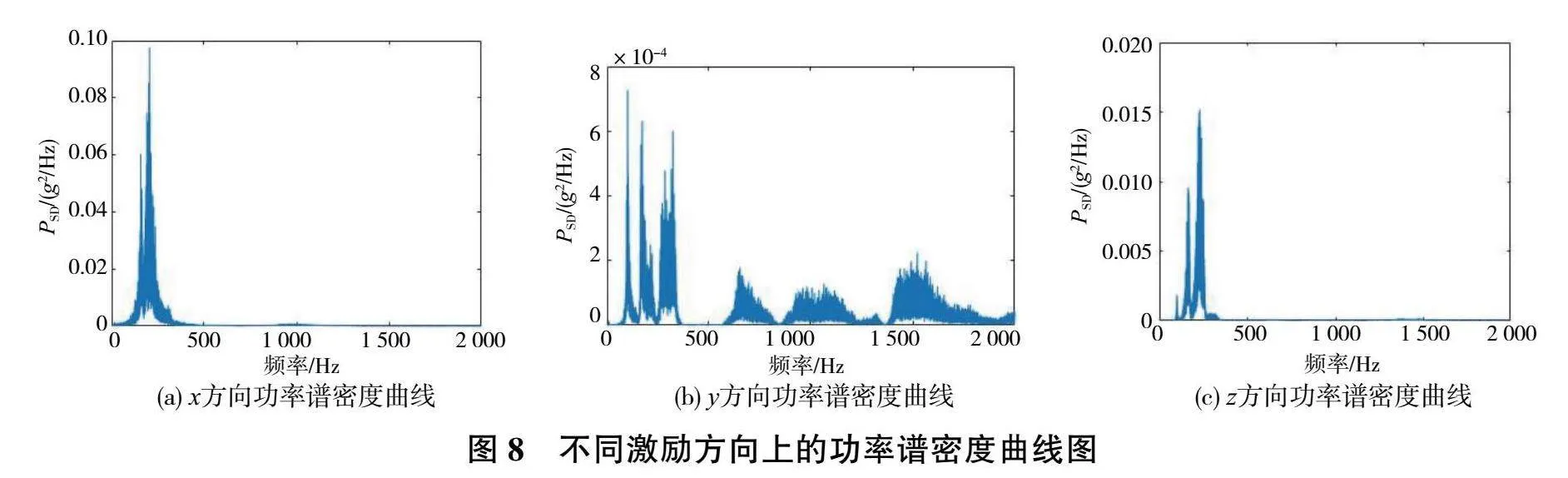
隨機振動的頻域分析是功率譜密度函數，功率譜密度函數是自相關函數的傅里葉變化，分別對3個方向上的時域數據進行頻域轉換，得到各自的功率譜密度曲線圖，如圖8所示。

從圖8中可以看出，功率譜密度在0～500Hz范圍內的低頻部分分布比例高，高頻部分比例低，線束振動能量主要集中分布在低頻部分。

3"軸向拉力表達式的確定

3.1"前提假設

為了減小問題分析的復雜程度，現對其模型做出如下假設：

1）線束沿卡箍軸向振動過程中不考慮線束松弛度，即不考慮線束下垂量帶來的影響；

2）線束內各導線具有相同的運動規律，各導線之間不存在相對運動；

3）與同一線束段裝配固定的兩個相鄰卡箍內產生的摩擦力相同。

3.2"數學計算模型

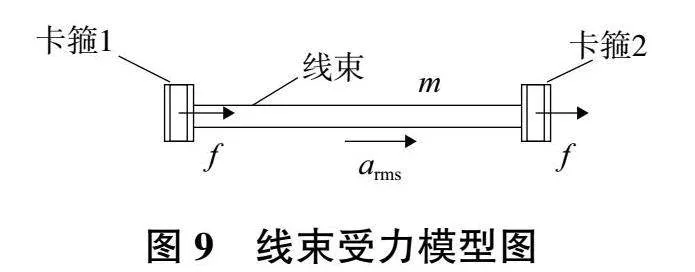
由時域加速度方均根振動數據可知，線束在卡箍軸線方向上的響應加速度方均根值最大，實際振動過程中引起的線束慣性力也最大，所以實際工作狀態下線束最易沿著卡箍軸向方向發生滑動松脫，引發卡箍固定失效。圖9為線束軸向振動受力模型圖，卡箍1和卡箍2分別作為線束的固定點安裝在飛機結構上。

線束在軸向方向的響應加速度方均根值為1.615 8g，要稍小于激勵加速度方均根值1.91g，這種現象的產生主要是由于卡箍上的橡膠襯墊造成的。根據橡膠材料的減震特性，振動能量由卡箍傳遞到線束的過程中，一部分能量通過橡膠襯墊的減震性消耗掉了，所以線束上的加速度響應值要小于振動激勵值。

通常情況下，振動試驗的參考譜是已知的，即激勵的加速度方均根值是已知的。如果忽略掉襯墊的減震效果，將激勵的加速度方均根值作為線束軸向響應的方均根值，即可以在非振動測試條件下獲取線束響應的時域統計量，減少試驗的次數，節約時間成本；同時加速度方均根值可以用來表示振動量級的大小，因此可以將隨機振動下的方均根值作為線束振動慣性力下的等效加速度來計算線束在振動過程中產生的慣性力。由圖9可知線束慣性力大小 ：

Farms=marms（1）

要使線束在振動過程中不會產生軸向滑動，相鄰卡箍內產生的摩擦力f：

2f=marms（2）

固定一段線束上的單個卡箍內所要產生的最小摩擦力fmin：

fmin=marms/2（3）

該摩擦力在數值上等于靜載荷條件下使線束從卡箍中滑動的軸向拉脫力。因此可以將該拉脫力的一半，即中等程度大小的拉脫力作為檢驗線束在卡箍內裝配可靠性的軸向拉力，計算式如下：

F=fmin/2=marms/4（4）

式中：arms為振動激勵的加速度方均根值；m為兩個相鄰卡箍之間的線束質量。

3.3"試驗驗證

線束隨機振動試驗譜加速度方均根值為1.91g，線束重量3N，代入式（4）中得軸向拉力：

F=marms4=1.43 N（5）

使用指針式推拉測力計的峰值模式測量線束剛好從卡箍內拉脫時的拉力值，測力計量程為100N，最小分度值為0.5N。試驗過程中將測力計拉力端與用單個卡箍固定的線束一端相連，沿卡箍軸線方向水平緩慢拉動線束直到線束在卡箍內產生滑動，記錄此時測力計的數值，如圖10所示。為減小試驗誤差，重復操作5次，得到表2所示數據。

試驗5次的平均值：

3.0+3.0+3.2+3.1+3.05=3.06 N（6）

根據線束拉脫力等于最大靜摩擦力的原理，單個卡箍實際接觸面內產生的最大靜摩擦力：

fs=3.06 N（7）

理論計算情況下，線束在單個卡箍內產生的最大摩擦力：

ft=2F=2×1.43=2.86 N（8）

兩者的相對誤差：

ft-fsfs×100%=6.54%（9）

理論與實際計算誤差在10%以內，可認為通過模型建立的拉力理論計算表達式是正確的。之后通過線束軸向拉力試驗驗證，在拉力F作用下線束在卡箍內不會產生軸向移動，即線束在卡箍內固定牢靠，證明了該方法的可行性。

4"結語

線束在機上裝配質量的可靠性對于飛機的安全適航有著非常重要的作用，本文基于對線束在隨機振動載荷下的響應數據分析，結合國外標準中拉力的檢驗方法，提出了一種用于計算線束裝配條件下的中等力計算檢驗方法，為實際生產實踐中線束在卡箍內的裝配可靠性提供一種檢驗方法。

參考文獻：

［1］ CCAR-25-R4中國民用航空規章第25部運輸類飛機適航標準 ［S］.

［2］ 池梁，閆靜，高科，等. 基于層次模型的線束裝配定位方法研究［J］. 機械制造與自動化，2019，48（3）：25-28，36.

［3］ 閆靜，顧嘉煒. 基于系統分離規則的線束通道研究［J］. 航空計算技術，2021，51（6）：112-116.

［4］ 鄭敏，王宗武，張艷，等. 航空卡箍選用裝配研究［J］. 航空標準化與質量，2015（2）：23-26，42.

［5］ 王丹，金鑫. 民用航空帶墊金屬卡箍的選用研究［J］. 中國科技信息，2016（12）：69-70.

［6］ SAE International， MIL-HDBK-522A， Guidelines for inspection of aircraft electrical wiring interconnect systems［S］.

［7］ SAE International，MIL-W-50881G，Wiring aerospace vehicle ［S］.

［8］ SAE International， SAE-AIR6808， Aerospace vehicle wiring， lessons Learned［S］.

［9］ 喬新愚，肖建紅，鄭術力. 隨機振動的描述方法及穩態檢驗［J］. 電子質量，2006（6）：33-35.

收稿日期：20221011