R20機器人仿真分析與試驗





摘"要:以串聯關節機器人為研究對象,根據機器人結構參數建立D-H法的機器人運動學模型,推導機器人運動學方程。使用ADAMS軟件對機器人進行動力學仿真分析,計算各關節驅動力矩隨時間變化的數據,將動力學計算的各關節最大動載荷作為機器人結構設計和有限元計算的力學條件,對機器人鑄件進行有限元仿真分析,搭建實驗平臺,對機器人位置重復性、姿態重復性、重復定位精度、位置穩定時間和位置超調量進行測試,對實驗數據進行整理和分析。仿真計算和實驗結果表明:該機器人設計合理,滿足設計指標要求。
關鍵詞:機器人;運動學;有限元;ADAMS
中圖分類號:TP242""文獻標志碼:A""文章編號:1671-5276(2024)02-0188-05
R20 Robot Simulation Analysis and Test
CHEN Pengwei1, GAO Fei2, WU Kai1
(1. School of Mechanical Engineering,Shaanxi Polytechnic Institute,Xianyang 712099,China;
2. College of Mechanical and Vehicle Engineering,Taiyuan University of Technology,Taiyuan 030024,China)
Abstract:Taking the serial joint robot as the research object, the robot kinematics model of D-H method is established according to the robot structural parameters to derive the robot kinematics equation. The dynamic simulation analysis of the robot is carried out using ADAMS software, the data of the driving torque of each joint changes with time is calculated, and the maximum dynamic load of each joint calculated by dynamics is taken as the mechanical condition of the robot structural design and finite element calculation to conduct finite element simulation analysis on robot casting. With the establishment of experimental platform, the robot's position repeatability, posture repeatability, repetitive positioning accuracy, position stability time and position overshoot are tested, an their experimental data are sorted out and analyzed. The simulation calculation and experimental results verify that the robot design is reasonable and meets the index requirements as designed.
Keywords:robot; kinematics; finite element; ADAMS
0"引言
工業機器人在工業制造、醫療、航空航天等領域得到越來越廣泛的應用[1]。六自由度串聯多關節工業機器人是一個復雜的多剛體系統[2]。眾多學者對機器人開展了大量的研究,如機器人構型設計分析[3]、機器人運動學分析[4]、機器人動力學建模和仿真[5-6]、機械臂運動精度關鍵技術的研究[7]、機器人運動及路徑規劃[8-9]、機器人標定方法及算法[10-11]等。
本文以負載能力20kg的六自由度串聯關節工業機器人R20為研究對象,在仿真計算數據和實驗數據基礎上對R20機器人性能及機器人設計分析方法的合理性進行試驗驗證。
1"機器人結構參數及運動學分析
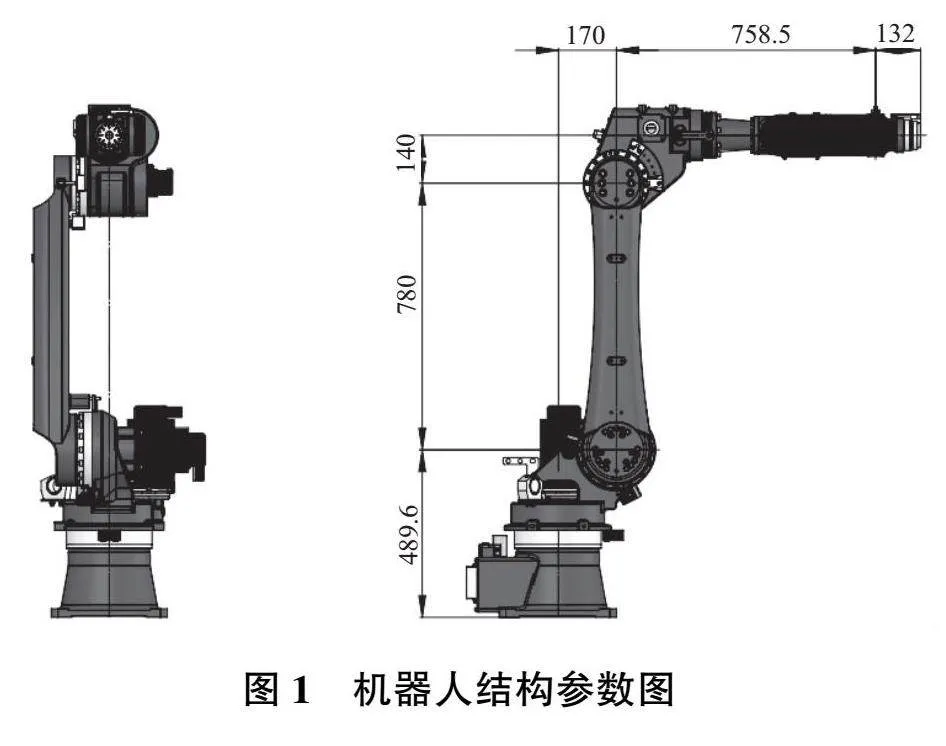
機器人機構構型為六自由度串聯關節機器人,機器人結構模型和參數如圖1所示。
采用Denavit-Hartenberg方法建立連桿坐標系,機器人笛卡兒坐標系如圖2所示,機器人的D-H參數、各軸最大轉動速度如表1所示。
建立D-H模型并進行運動學推導,求解機器人末端坐標系到基坐標系的齊次變換矩陣隨各關節軸的變化關系。
i-1"iT=ci-sicosαisisinαiaici
sicicosαi-cisinαiaisi
0sinαicosαidi
0001(1)
機器人各連桿之間D-H參數坐標系變換矩陣:
01T=c10s1a1c1
s10-c1a1s1
0100
0001"12T=c2-s20a2c2
s2c20a2s2
0010
0001
23T=c30s3a3c3
s30-c3a3s3
0100
0001"34T=c40s40
s40-c40
010d4
0001
45T=c50-s50
s50c50
0-100
0001"56T=c6-s600
s6c600
0010
0001
(2)
從末端坐標系依次向前做齊次變換得末端坐標系到基坐標系的變換關系:
06T=01T12T23T34T45T56T(3)
將其簡要表達為
06T=nxoxaxpx
nyoyaypy
nzozazpz
0001(4)
式中:ci表示cosθi;si表示sinθi;nxoxax
nyoyay
nzozaz為姿態矩陣;pxpypz 為位置向量。
2"機器人動力學計算
以串聯關節機器人為研究對象,由拉格朗日法知,機器人的動力學方程的矩陣形式為
D(θ)θ··+C(θ,θ·)θ·+G(θ)=M(5)
式中:D(θ)為機器人系統的慣性矩陣;C(θ,θ·)為機器人系統的向心力和科里奧利力項;G(θ)為機器人系統的重力矩陣;M為機器人系統的外力矩陣。
使用多體動力學軟件ADAMS進行仿真計算,機器人末端負載20kg,關節的最大轉動速度如表1所示,機器人虛擬樣機模型及實物樣機如圖3所示。
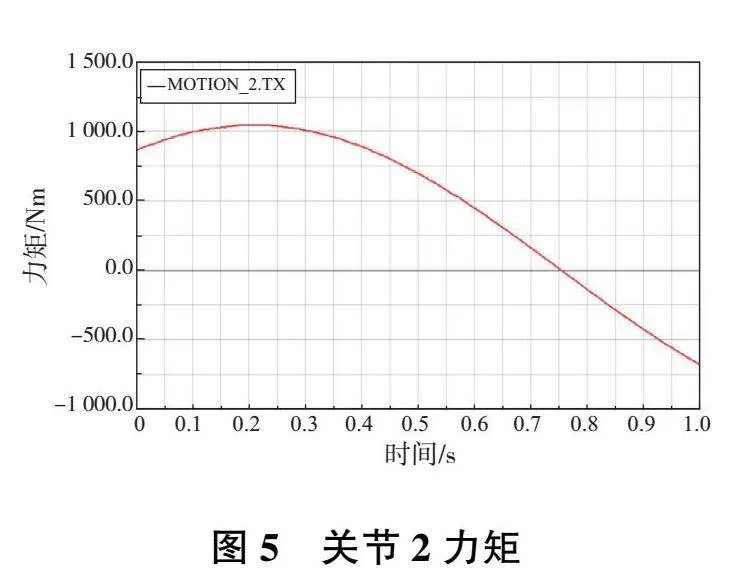
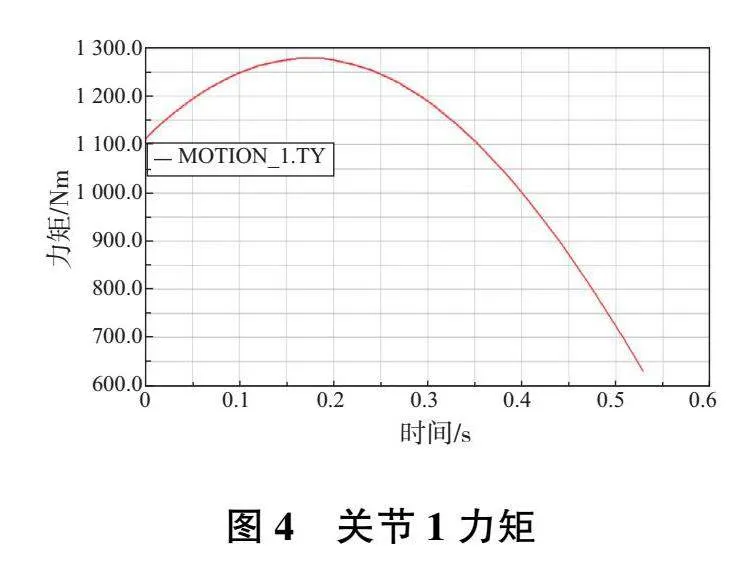
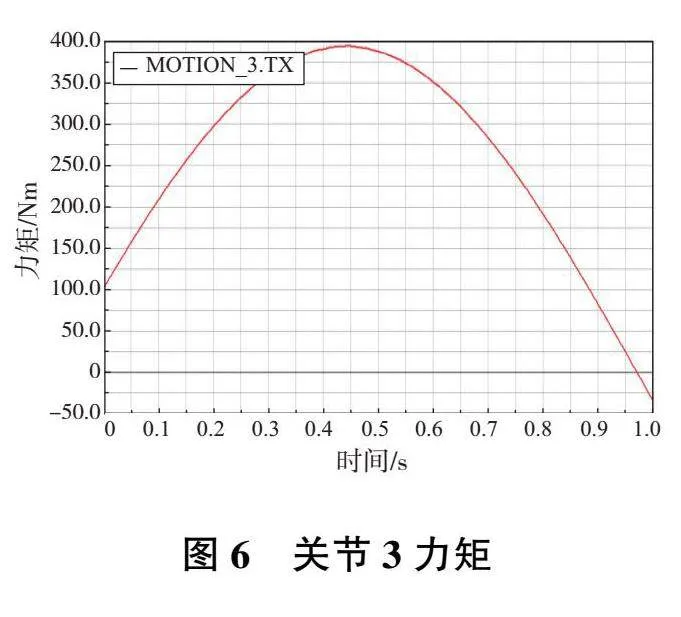
機器人前3個關節動力計算結果數據曲線如圖4—圖6所示。
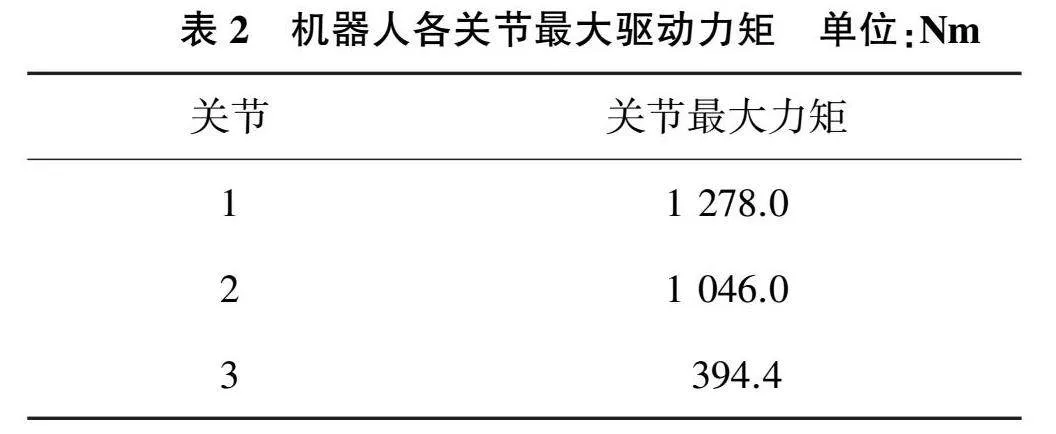
在圖4—圖6數據曲線中提取機器人各關節最大驅動力矩值如表2所示。
3"機器人結構件有限元分析
機器人作業過程中,機器人鑄件的結構力學性能對機器人運動穩定性和運動精度有著較大的影響,因此對機器人主要鑄件進行結構力學分析十分必要。
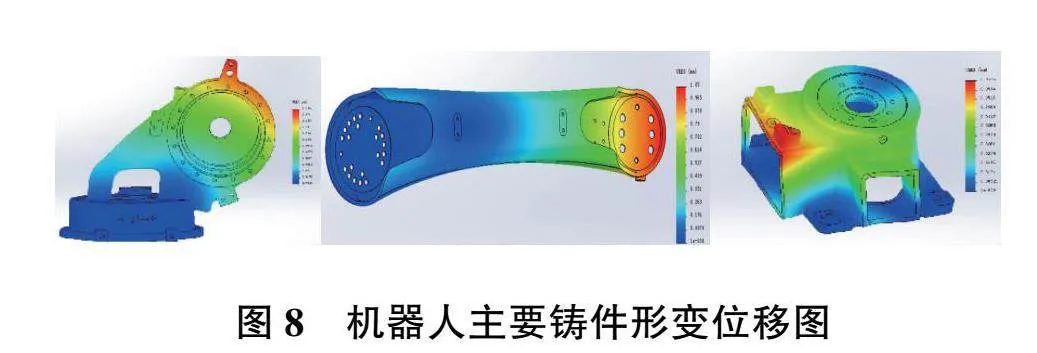
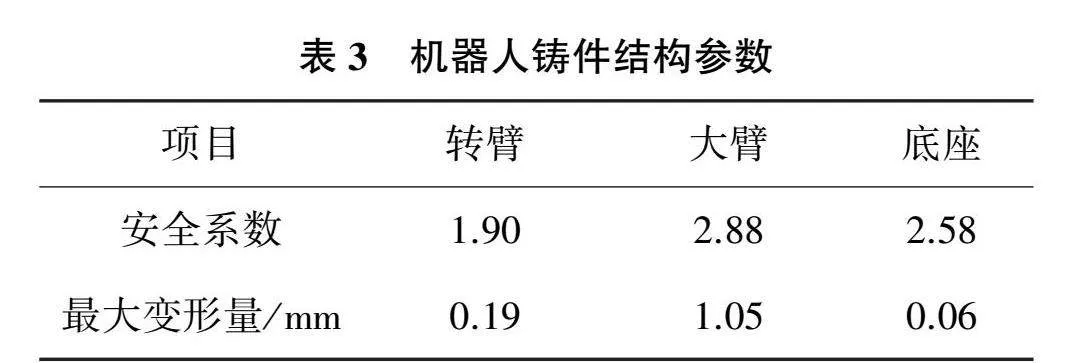
以動力學計算取得的機器人各關節力矩數據作為各鑄件的負載依據,如圖7—圖8及表3所示。根據FEA算法對機器人主要鑄件進行有限元計算。
機器人鑄件結構力學計算結果顯示,機器人大臂變形量為1.05mm,在鑄件中變形量最大,機器人鑄件最小安全系數1.90,滿足設計要求。
4"實驗與分析
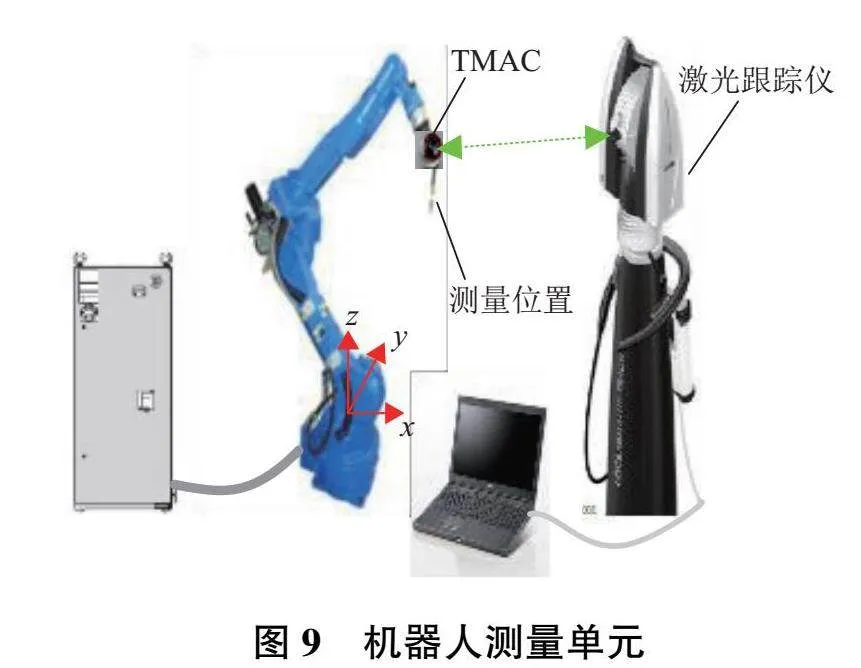
依據《GB/T 12642—2013工業機器人性能規范及其試驗方法》,對機器人位置重復性、姿態重復性、重復定位精度,位置穩定時間和位置超調量進行實驗,測量單元如圖9所示,機器人實驗平臺如圖10所示。機器人末端安裝TMAC,使用Leica AT960-MR激光跟蹤儀實時測量機器人末端運行軌跡。
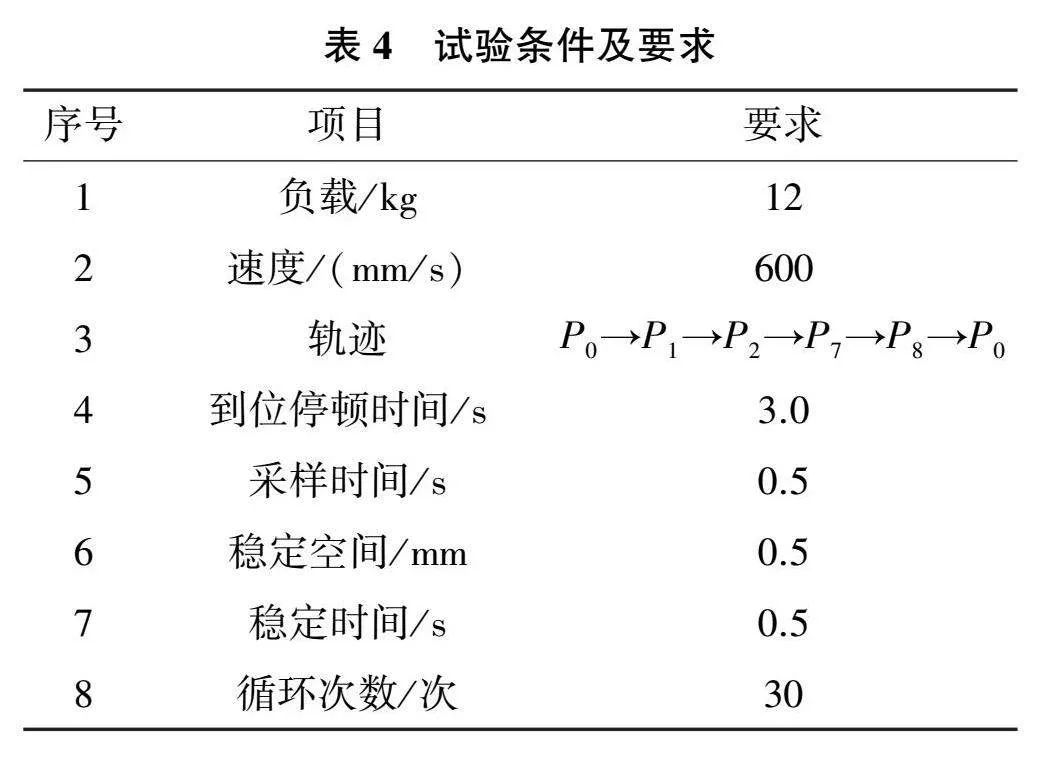
1)試驗條件:試驗條件如表4所示。
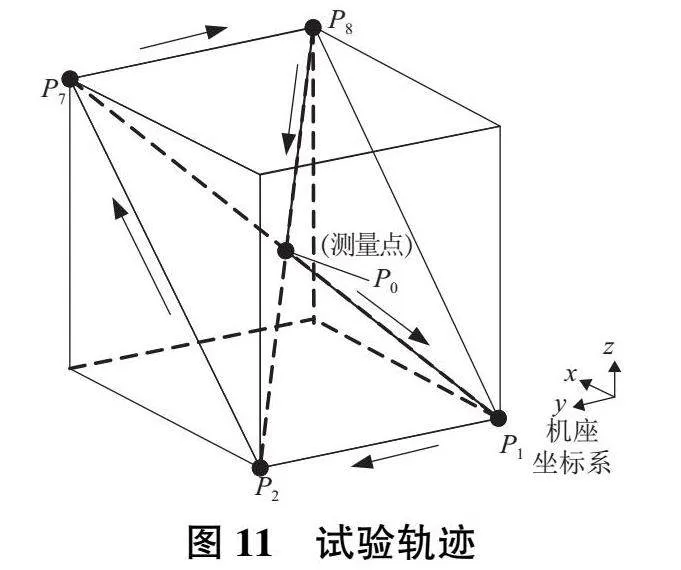
2)試驗軌跡:試驗軌跡采用矩形軌跡,如圖11所示。
4.1"位置重復性、姿態重復性和重復定位精度
1)位置重復性
到位停留時間為3s時,矩形軌跡P1、P2、P7、P8、P0 5點的位置重復性如表5所示。
2)姿態重復性
到位停留時間為3s時,矩形軌跡P1、P2、P7、P8、P0 5點繞x、y、z 3個方向的姿態重復性如表6所示。
3)重復定位精度
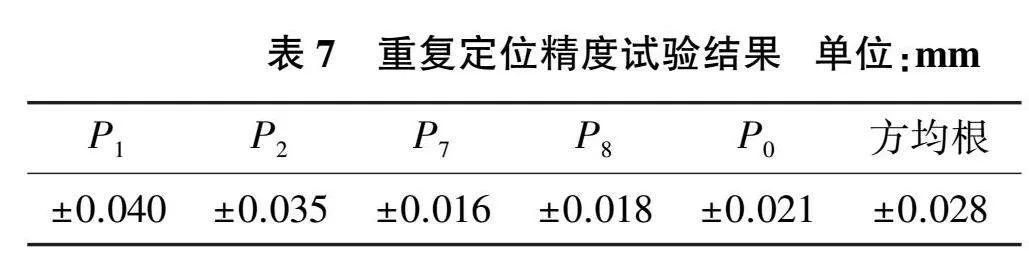
到位停留時間為3s時,矩形軌跡P1、P2、P7、P8、P0 5點的重復定位精度如表7所示。
4.2"位置穩定時間和位置超調量
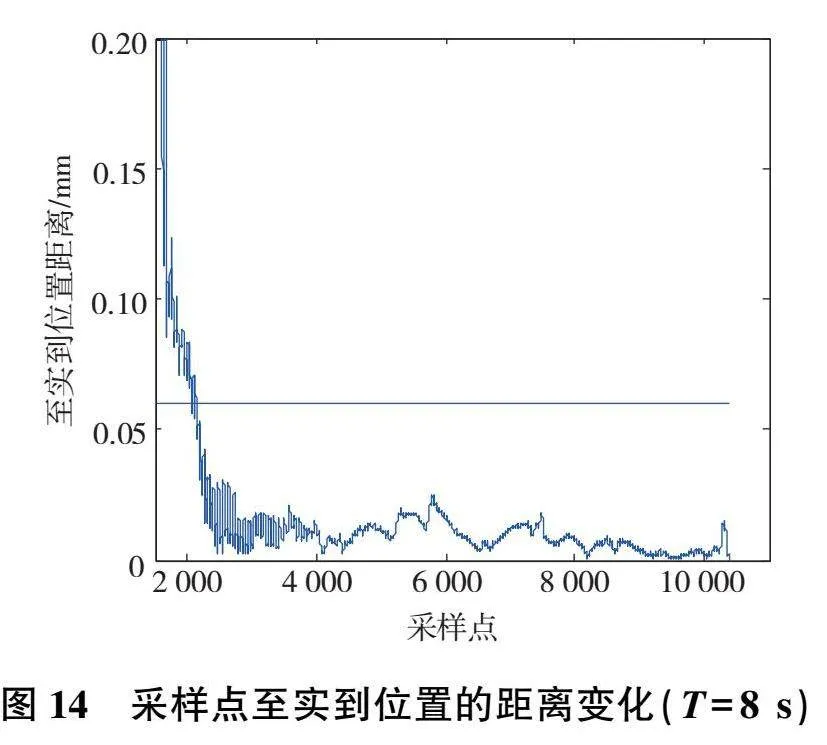
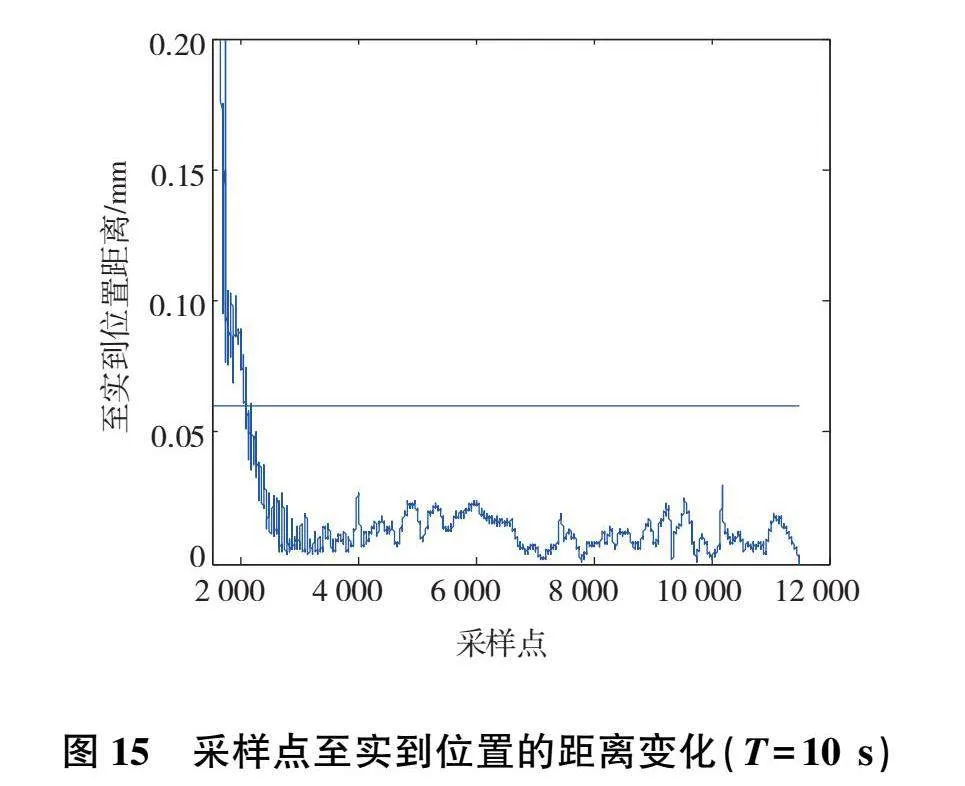
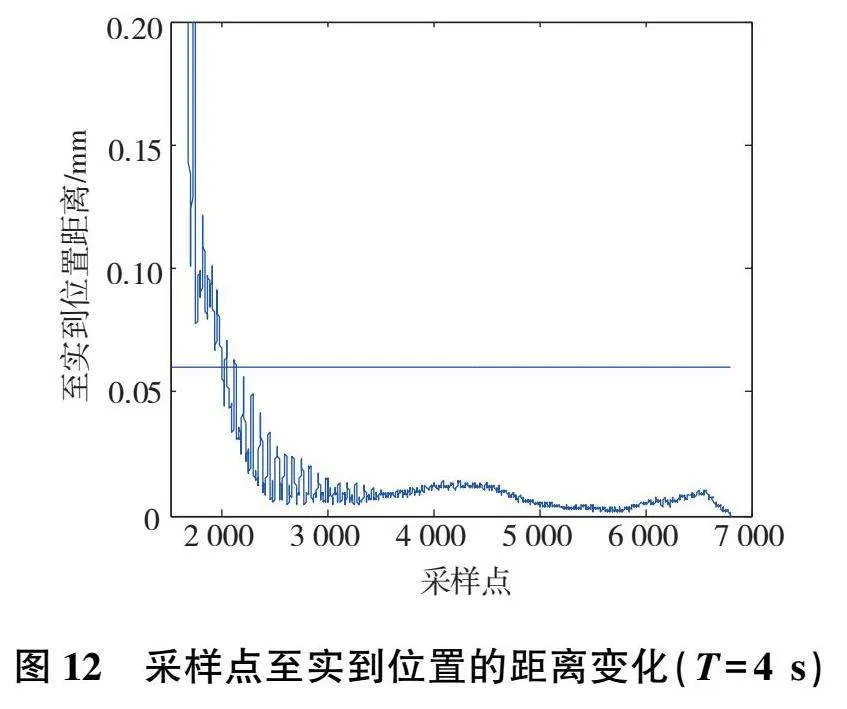
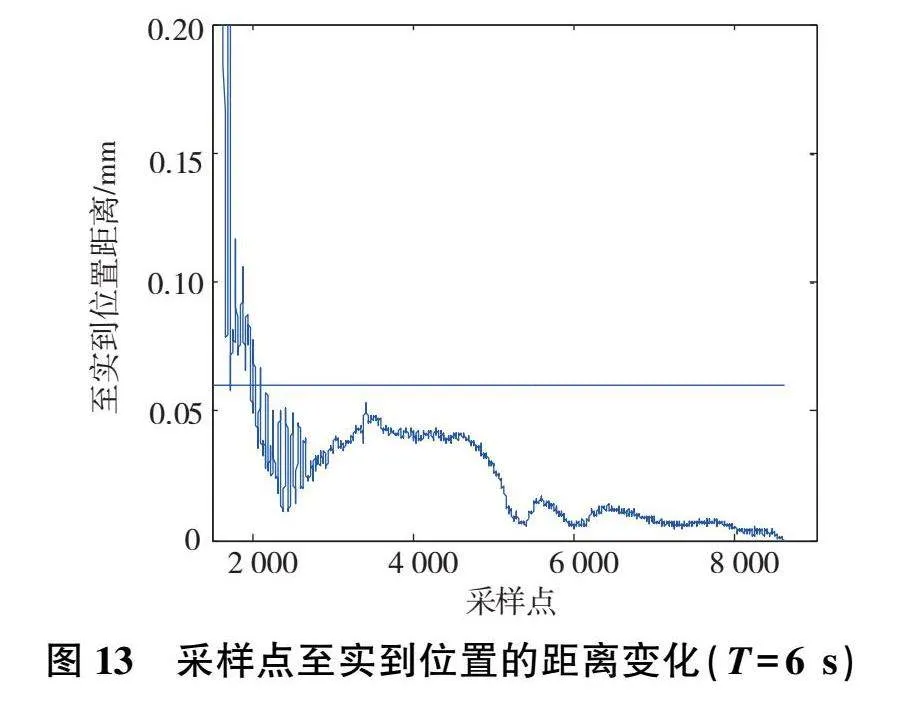
多次測量到達P0點時采樣點至實到位置的距離變化如圖12—圖15所示。
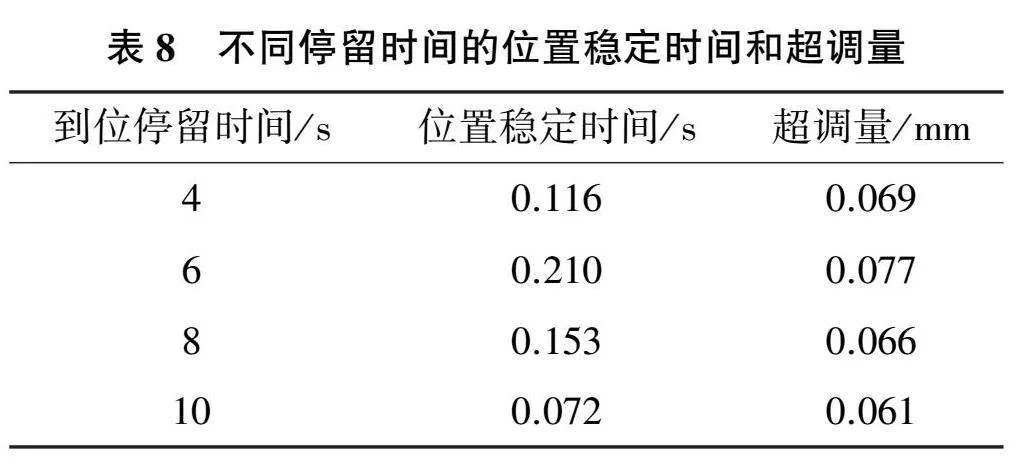
機器人到位停留時間的位置穩定時間和超調量計算結果如表8所示。機器人位置穩定時間較短,機器人到位無超調現象。
5"結語
本文以20kg負載能力的六自由度串聯關節工業機器人為研究對象,根據串聯關節機器人結構參數和機構特點,采用Denavit-Hartenberg方法建立連桿坐標系,進行機器人運動學分析;使用多體動力學軟件ADAMS計算了機器人關節的驅動力矩,各計算關節加減速力矩軌跡,其曲線連續且比較平穩,表明了各關節動力學設計和運動學規劃的合理性。以計算所得的最大動力矩作為結構有限元設計的力學輸入條件,對機器人主要鑄件進行結構設計和有限元分析,有限元分析結果表明了機器人鑄件結構力學設計的合理性。
搭建機器人實驗平臺,由實驗結果驗證了該機器人具有良好的性能。機器人設計合理,仿真分析和實驗方法可以為同類機器人的研究提供支撐。
參考文獻:
[1] 潘敬鋒,訾斌,王正雨,等. 基于試驗與仿真聯合分析的噴涂機器人軌跡精度可靠性研究[J]. 機械工程學報,2020,56(19):210-220.
[2] 新松機器人自動化股份有限公司.柔性多關節機器人[EB/OL]. (2015-11-06)[2022-11-15]. http://www.siasun.com/ product/industrial robot/product 201511 06093319.htm1.
[3] 田勇,王洪光,潘新安,等. 協作機器人的構型分析研究[J]. 智能系統學報,2019,14(2):217-223.
[4] 朱慶浩,臧強,岳華,等. 6R工業機器人的運動學分析與仿真[J]. 中國科技論文,2020,15(8):953-958.
[5] 郭忠峰,李文龍,郭輝,等. 軸承環鍛壓操作機器人運動學分析與動力學仿真[J]. 制造技術與機床,2020(8):13-16.
[6] 沈國棟. 考慮關節柔性的六自由度串聯工業機器人動力學建模與末端抖動抑制[D]. 濟南:山東大學,2020.
[7] 王琨. 提高串聯機械臂運動精度的關鍵技術研究[D]. 合肥:中國科學技術大學,2013.
[8] MOE S,GRAVDAHL J T,PETTERSEN K Y. Set-based control for autonomous spray painting[J]. IEEE Transactions on Automation Science and Engineering,2018,15(4):1785-1796.
[9] 關英姿,劉文旭,焉寧,等. 空間多機器人協同運動規劃研究[J]. 機械工程學報,2019,55(12):37-43.
[10] 周星,黃石峰,朱志紅. 六關節工業機器人TCP標定模型研究與算法改進[J]. 機械工程學報,2019,55(11):186-196.
[11] 韓奉林,江曉磊,嚴宏志. 基于可測距平板工具的機器人TCP標定方法[J]. 計算機工程與應用,2016,52(18):18-23.
收稿日期:20230117

