基于模型的渦扇發動機性能衰減評估

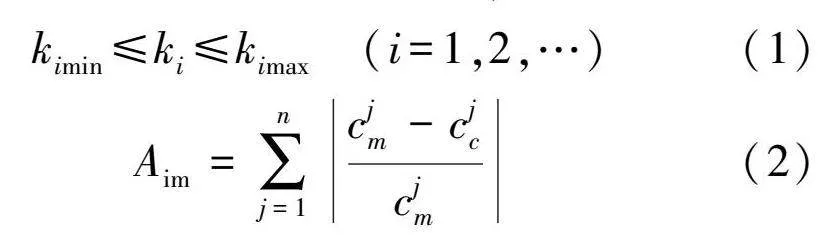
摘"要：為了獲得渦扇發動機壽命期內各部件性能衰減程度與衰減趨勢，基于發動機性能計算模型與部件特性衰減因子，采用序列二次優化算法對1臺300 h持久試車的發動機各階段部件性能衰減情況進行尋優計算。計算結果表明：模型計算結果與試驗測量結果誤差最大為4.33 %，絕大部分參數誤差在±2.0 %范圍；高壓部件持久試車前期衰減，后期低壓部件衰減較快，300 h試車后壓氣機與低壓渦輪衰減最嚴重。

關鍵詞：渦扇發動機；性能衰減；衰減因子；序列二次優化算法；持久試車

中圖分類號：V231""文獻標志碼：A""文章編號：1671-5276（2024）02-0224-05

Model-based Performance Degradation Evaluation for Turbofan Engine

ZHAO Weichen， WANG Chen， LI Zhaohong， YANG Huaifeng， WANG Jun

（AECC Shenyang Engine Research Institute，Shenyang 110066，China）

Abstract：In order to obtain the performance degradation and degradation trend of each component in turbofan engine life cycle， sequential quadratic optimization algorithm based on engine performance calculation model and component degra-dation factors was used to optimize the performance degradation in each stage of a 300 hour long-term test engine. The calculation results show that the maximum error between the model calculation results and the experimental measurement results is 4.33%， and the error of most parameters is within ± 2.0%. In the earlier stage of long-term test， the high-pressure turbine and compressor decay， the low-pressure turbine and fan components decay faster in the later stage and the compressor and low-pressure turbine decay most seriously after 300 hours test.

Keywords：turbofan engine；performance degradation；degradation factors；sequential quadratic optimization algorithm；long-term test

0"引言

航空發動機工作包線廣、工作環境因素復雜，在使用過程中存在流路部件磨損、燒蝕、積垢等情況。這些因素會造成航空發動機壽命期內推力降低、耗油率升高等性能損失。對于軍用航空與民用航空領域，航空發動機壽命期內性能衰減與保持情況均是一項關鍵指標。研究航空發動機性能衰減情況對使用安全性與壽命期內維修經濟性有重要意義，但發動機各部件工作環境差異較大，在壽命期內衰減程度與衰減速率并不相同。

近年來國內外眾多學者與工程技術人員致力于發動機性能衰減與退化研究，分為基于數據驅動與基于發動機模型驅動兩種。WANG P等［1］、唐王［2］與黃亮［3］先后采用數據驅動方法利用熱力測量參數計算發動機剩余壽命。王鐘毓［4］采用數據驅動方法計算發動機裝機性能趨勢。ZIYA M S等［5］基于發動機模型，研究用流路部件衰減表征發動機性能衰減的方法。D?RING F等［6］基于壓氣機長試試驗數據提出一種考慮衰減的壓氣機特性修正方法，并指出可應用于整機性能衰減評估。林學森等［7］基于渦軸發動機性能模型，通過設定部件特性退化因子計算發動機性能參數，以修正后模型為數據源，開展ELM模型訓練和測試，用于性能退化診斷，平均診斷精度達97.5%。黃開明等［8］采用非線性氣路分析法計算渦軸發動機長試過程壓氣機與渦輪4個特性修正參數衰減情況。ARETAKIS N等［9］基于商用渦扇發動機模型與試驗數據，采用PNN方法訓練含8個修正參數的健康評估模型。ROUMELIOTIS I等［10］進一步基于該方法利用4個參數對某燃氣輪機兩年內性能變化進行評估。徐田鎮［11］基于發動機性能模型，利用三維線性插值法（馬赫數、燃油流量、高度）以5個參數表征部件退化程度，在亞音速與超音速兩類工況部件退化參數計算誤差小于3%，性能參數誤差小于2%。錢俊寧［12］與李永進［13］基于性能模型，利用卡爾曼濾波器分別使用四五個部件性能退化參數實時計算發動機性能。楊思幸［14］采用自適應擬合法改進卡爾曼濾波器，對4個部件共計8個參數的退化情況進行計算驗證，指出采用多部件多退化參數評估性能的準確性高于單部件單參數評估。夏天乾等［15］設計一種基于動態逆的健康參數估計方法，搭配神經網絡建立渦軸發動機自適應模型，相比線性卡爾曼濾波器具有實時性更高的優點，減少耗時26%。

已公開的發動機持久試車試驗數據極其缺乏，國內對性能衰減研究注重于性能預測與故障診斷模型或工具開發，適用性及準確性尚需驗證。隨著我國軍用與民用航空發動機與燃氣輪機產品逐漸成熟，產品大量使用凸顯出性能衰減研究的急迫性。本文利用某小涵道比渦扇發動機300h持久試車試驗數據，基于發動機模型與部件衰減因子開展發動機性能衰減研究，可為發動機壽命期內維修周期設計和流路部件衰減機理研究提供支撐。

1"發動機控制規律與參數說明

本文研究的發動機類型為某小涵道比渦輪風扇發動機，發動機的主調節參數包括高壓物理轉速、低壓物理轉速與低壓渦輪后排氣總溫，中間及以上狀態中的1個參數受限，其他2個參數隨動，可通過控制計劃調整發動機性能。發動機可調幾何控制參數包括風扇、壓氣機進口可變彎度整流葉片角度α1、α2和噴管喉道面積A8。通過部件特性測量試驗檢測壓縮部件設計角度與非設計角度部件性能，折算葉片角度調節與壓縮部件換算流量、壓比、壓縮效率變化的映射關系，在其他非試驗測量中用轉速插值計算部件工作特性。

利用發動機地面臺架試車數據修正模型中流路總壓損失、引氣流量系數等參數，使性能計算模型所計算的發動機性能參數與典型截面氣動熱力參數滿足工程研究精度要求。

2"基于發動機模型的衰減評估方法

隨著發動機使用時間的增加，各部件存在性能衰減情況，綜合表現效果是發動機整機推力降低、耗油率升高。基于發動機性能計算模型，引入部件特性衰減因子衡量部件特性變化情況。以發動機環境參數為模型輸入參數，以發動機臺架試驗性能參數與截面氣動熱力測量參數為目標值，根據多臺份持久試車發動機分解后部件試驗特性測量結果設定衰減因子范圍，在衰減因子調節范圍內通過發動機性能模型計算獲得一組解與目標測量相比，滿足精度要求，故認為該工況下部件特性衰減因子可以表征當前發動機部件性能衰減情況。該問題是一個性能尋優問題，優化方程如下：

kimin≤ki≤kimax"（i=1，2，…）（1）

Aim=∑nj=1cjm－cjccjm（2）

式中：ki表示部件特性衰減因子；i表示衰減因子數目；kimin與kimax表示衰減因子取值邊界；cjm表示試驗測量參數，包括發動機性能參數與截面氣動熱力參數；j表示測量參數數目；cjc表示性能模型對應計算結果。優化流程如圖1所示。

發動機部件性能影響因素包括非旋轉部件特性因素和旋轉部件特性因素，非旋轉部件特性因素表現為總壓損失、燃燒效率等，旋轉部件特性因素表現為流量、效率等［16］。本文開展的研究未設置流路總壓損失與燃燒室燃燒效率衰減因子，設置了4個旋轉部件中共8個衰減因子，分別用k1—k8表示，具體對應關系見表1。

3"序列二次優化算法驗證

部件性能衰減因子尋優方法采用序列二次優化算法，序列二次優化算法是通過求解一系列二次規劃子問題得到目標函數最優解的方法。該方法在求解含有約束的非線性優化問題時具有收斂性強的特點。

為了驗證優化算法對求解發動機衰減問題的適用性，首先利用發動機性能模型，以環境參數與部件衰減因子為給定輸入，計算獲得發動機性能與氣動參數。以該組參數為目標函數，在預設衰減因子范圍內進行求解，校核修正因子偏差范圍。模型梯度使用有限差分法計算，相對步長選取10-4。

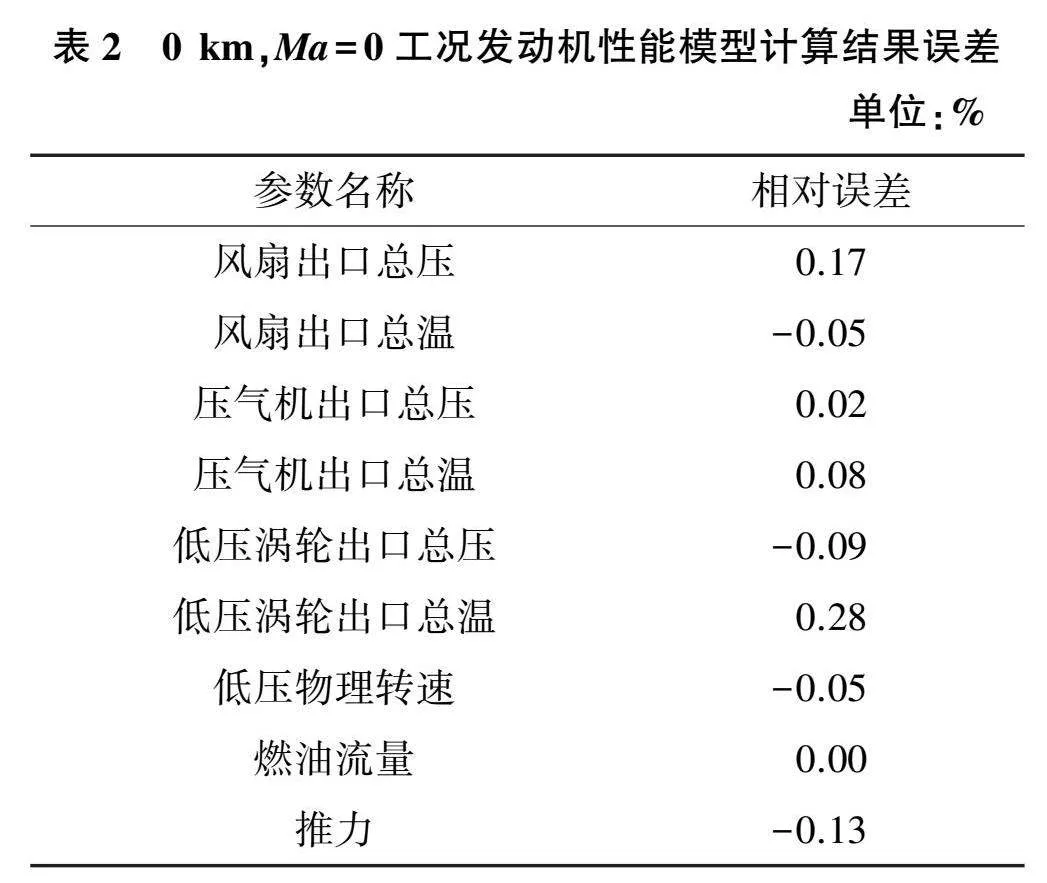
表2是0km、Ma=0工況給定衰減因子后模型計算結果與尋優后模型結果對比，目標函數選用發動機3個性能參數（低壓物理轉速、燃油流量、推力）和6個截面氣動熱力參數（風扇、壓氣機、低壓渦輪出口總溫、總壓），輸入參數為標準大氣環境溫度、壓力和高壓換算轉速。誤差最大的參數為低壓渦輪出口溫度，相對誤差為0.28%。表3是序列二次優化算法尋優結果，部件特性衰減因子中流量衰減因子與給定值誤差較大，達到1.1%。考慮到目標函數中無流量參數，根據性能計算模型中流量平衡關系，壓氣機部件流量特性修正誤差會保持至軸向下游高壓渦輪、低壓渦輪部件流量修正因子。

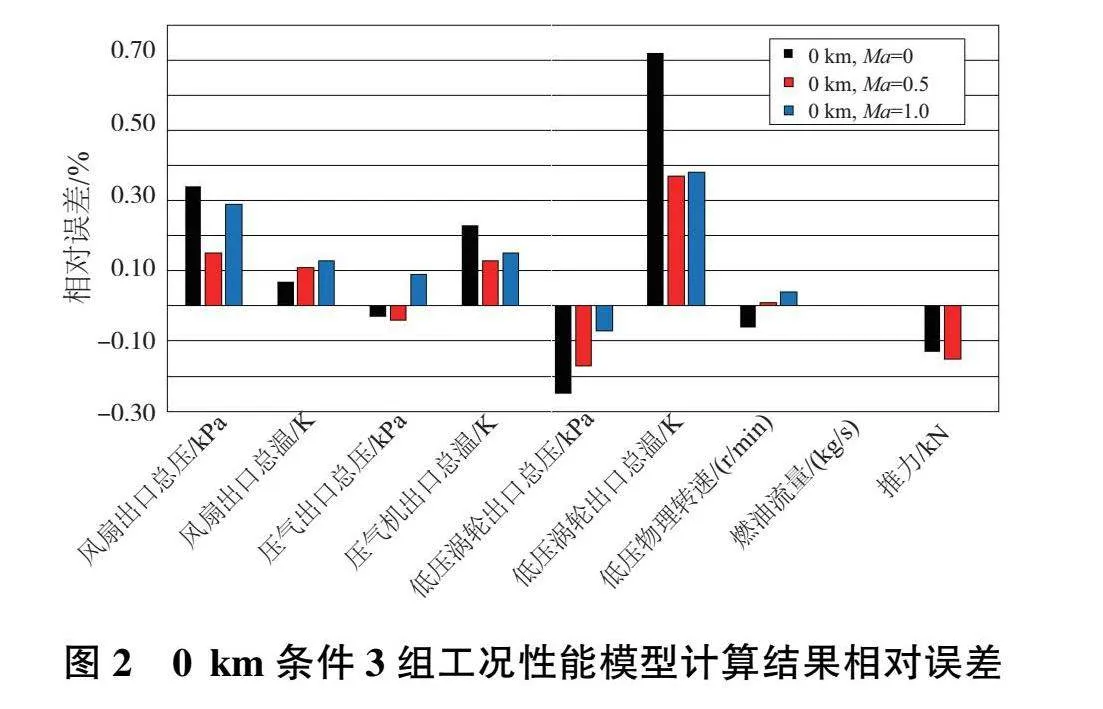
進一步選取同一組部件衰減因子的3個工況點參數作為給定輸入，利用性能模型計算相同結果參數。以3個工況下計算結果參數作為目標函數，求解部件衰減因子并校核偏差。選取高度0km，馬赫數0、0.5、1的3個工況，模型計算結果誤差如圖2所示。尋優目標點增加為3個后，相同收斂標準下計算誤差增加但均不超過1.0%，3組結果誤差最大項均為低壓渦輪出口總溫，0km、Ma=0工況相對誤差為0.72%。

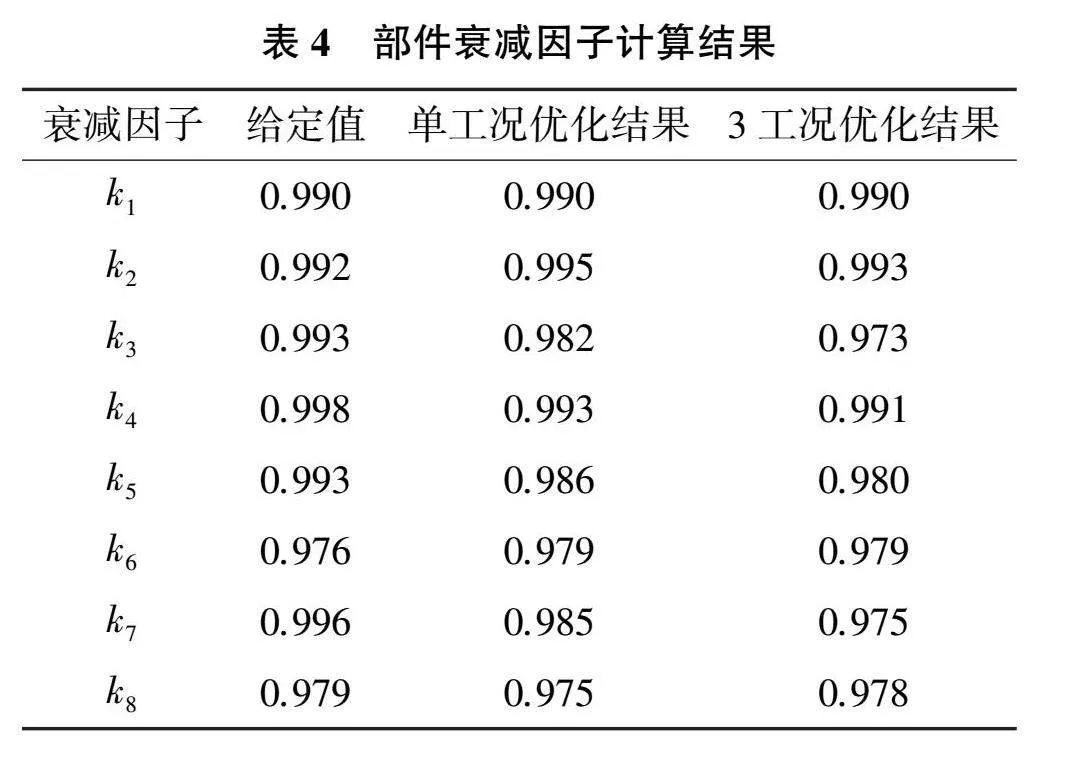
從表4衰減因子尋優結果觀察到：考慮3個工況后部件流量系數衰減因子與給定值的誤差進一步增大，并出現與單工況尋優相同的誤差保持效果。3工況尋優的壓氣機流量衰減因子為0.973，與給定值相差2.0%，在目標函數中無流量約束情況下流量修正因子誤差較大。序列二次優化算法作為一種局部尋優算法，在以多工況點參數作為目標函數時會引入更多局部次優解，增大尋優誤差。以該方法進行多工況尋優時，應分工況優化并合理給定初值與尋優范圍。

4"發動機300h性能衰減計算

基于發動機性能計算模型與對應發動機持久試車數據開展發動機300h性能衰減計算。試驗數據選取發動機持久試車過程中每100h的性能錄取結果，每個時間階段選取暖機后2個狀態點：中間狀態與高壓相對換算轉速為0.97狀態。兩狀態轉速相近，認為部件特性衰減程度相當。

目標函數選用發動機2個性能參數（低壓物理轉速、推力）和風扇、壓氣機、低壓渦輪出口截面7個氣動熱力參數。輸入環境與控制參數為環境靜壓、發動機進口總溫與總壓、風扇和壓氣機進口整流葉片角度、噴管面積、高壓物理轉速。整流葉片角度、噴管面積可調幾何參數用于計算與控制計劃給定值的偏差量，角度偏差量以特性修正方式考慮進模型，噴管面積偏差通過調整落壓比控制計劃方式加入發動機性能模型。

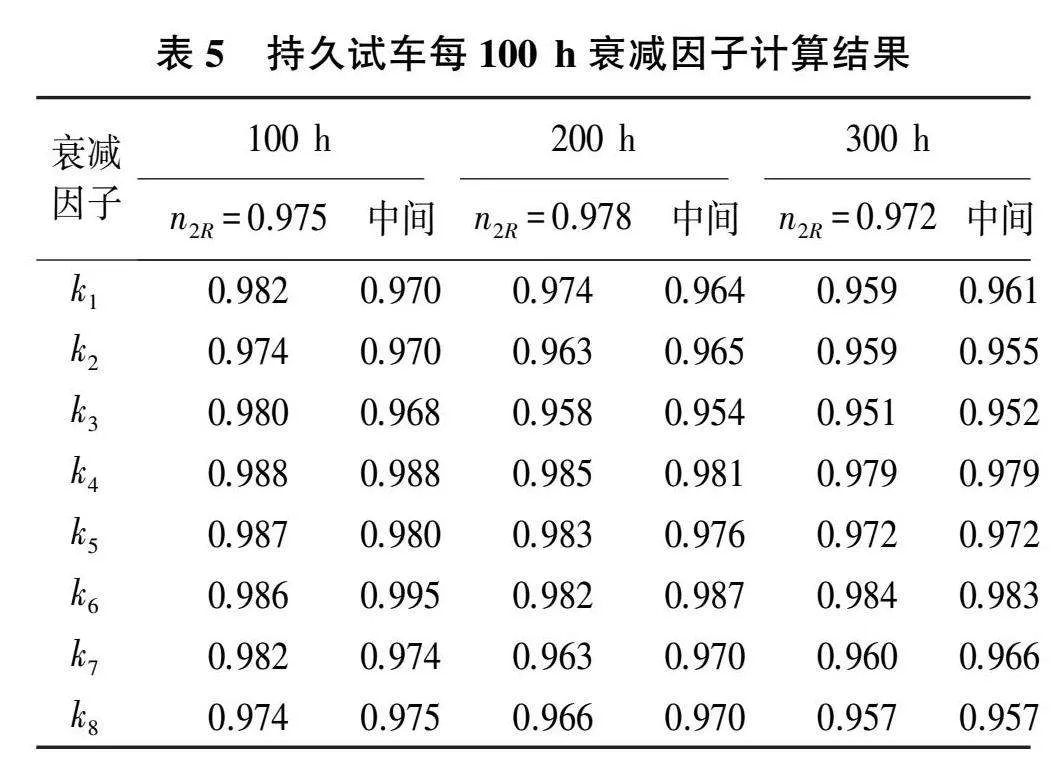
計算過程首先利用100h試驗測量數據進行衰減因子尋優，獲得兩種狀態尋優結果后取各衰減因子的高值作為200h優化過程中各衰減因子取值上邊界，進一步取200h計算結果中高值作為300h后，尋優過程各衰減因子取值上邊界。該取值方法是基于同一發動機在持久試車過程中部件換算流量、換算效率持續衰減或穩定不變的假設。發動機持久試車過程中各階段中間狀態、高壓相對換算轉速（n2R）0.97狀態的衰減因子計算結果如表5所示，100h階段風扇與壓氣機流量衰減因子在兩種狀態下尋優差異最大，以中間狀態尋優結果為基準時相對誤差均為1.24%；200h階段風扇流量衰減因子相對誤差最大達到1.04%；300h階段低壓渦輪流量衰減因子相對誤差最大達到-0.62%，高壓壓氣機與高壓渦輪部件特性衰減因子基本一致，相對誤差在0.1%量級。在發動機衰減程度較低時，各轉速狀態下對部件衰減因子敏感性高，即存在多種部件衰減情況符合目標發動機性能表現。在發動機衰減程度較大，如使用300h及以上時，發動機各轉速狀態下對部件特性衰減因子敏感性低。

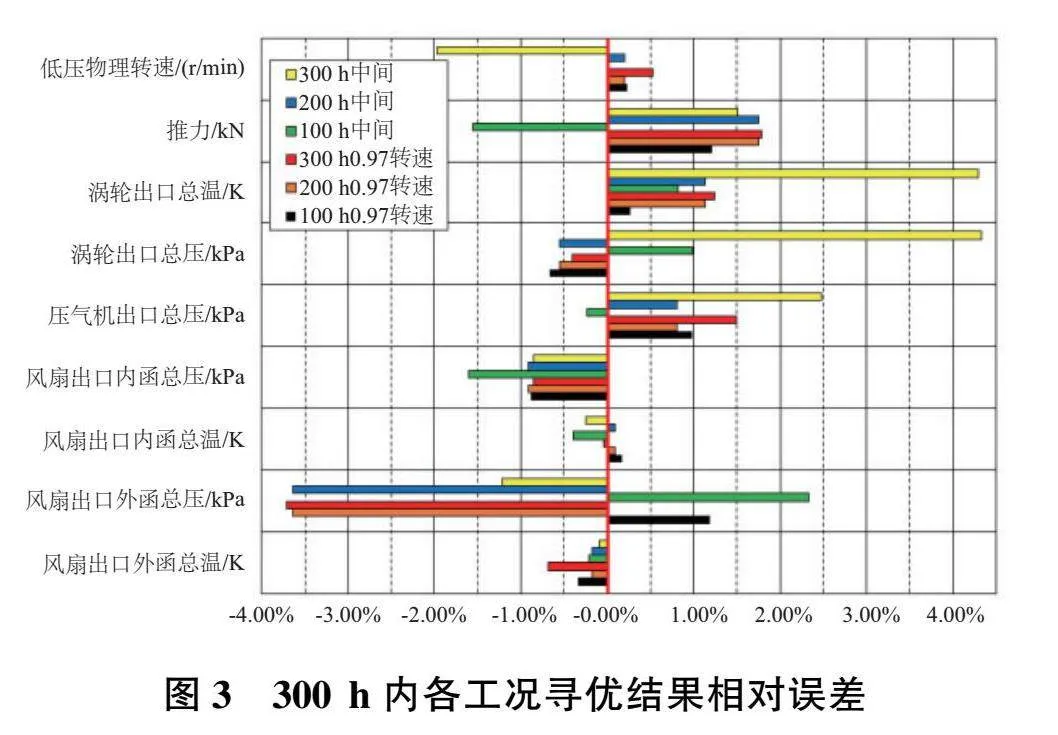
上述6個工況點尋優結果相對誤差如圖3所示，與目標參數的誤差均在±4.0%范圍，最大達到4.33%，大部分參數處于±2.0%偏差范圍內。在保證相似工況衰減因子差異的基礎上，該方法可應用于發動機性能衰減工程分析使用。與試驗數據對比發現300h中間狀態低壓渦輪出口總溫、總壓與低壓物理轉速相對誤差較大，原因是在長時間使用后，噴管出現塑性變形，噴管面積是尋優輸入參數，噴管面積偏差造成了低壓級參數匹配的差異。同時，在長試后對壓氣機進口可調導葉進行調節以保證發動機性能，但模型中輸入的部件特性修正量未考慮性能衰減，因此在發動機可調幾何存在變化時尋優誤差會增大。

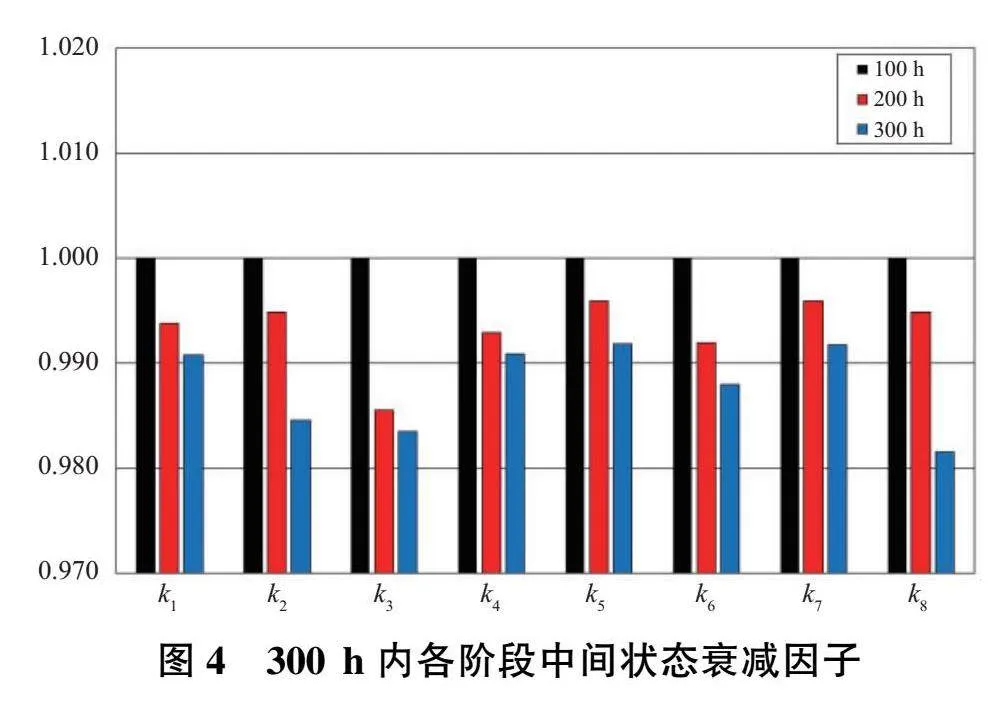
試驗用發動機在進行持久試車前已使用一段時間，并非完全新機狀態。以持久試車前100h中間狀態部件衰減因子為基準，對200h與300h中間狀態部件衰減因子進行歸一化處理，處理結果如圖4所示。隨使用時間增加，前期核心機部件開始衰減得較明顯：壓氣機流量、效率、高壓渦輪效率下降更快；后期使用至300h后，高壓部件小幅衰減，低壓部件如風扇效率、低壓渦輪效率下降明顯。根據長試發動機調試經驗，長試后壓氣機清洗可有效恢復發動機性能，可進一步分解研究低壓部件效率下降原因，為返修發動機提供指導方向。

5"結語

本文介紹了一種基于發動機性能計算模型與部件特性衰減因子的發動機性能衰減評估方法。基于修正后發動機性能計算模型，利用序列二次優化算法，驗證部件衰減因子計算精度與有效性。進一步結合持久試車發動機試驗數據，計算300h內部件衰減情況，得出以下主要結論：

1）部件性能衰減選取風扇、壓氣機和高低壓渦輪流量、效率衰減因子，經模型驗證采用序列二次優化算法進行尋優時，單個工況點截面氣動參數計算結果最大誤差為0.28%，3個工況點誤差升高，最大為0.72%，對于多工況點尋優應進一步引入非旋轉部件特性修正因子用來降低尋優誤差；

2）在發動機300h持久試車過程中，每100h后部件衰減因子尋優的結果一致性較高，隨使用時間增加相似狀態衰減因子相對誤差由1.24%下降至-0.62%；300h內6個工況點尋優計算結果與試驗誤差最大4.33%，絕大部分參數相對誤差在±2.0%范圍；

3）發動機300h持久試車前期高壓部件衰減較快，300h試驗后期風扇、低壓渦輪效率衰減較快；其中壓氣機流量、低壓渦輪效率衰減最嚴重。

參考文獻：

［1］ WANG P，GAO R X. Markov nonlinear system estimation for engine performance tracking［J］. Journal of Engineering for Gas Turbines and Power，2016，138（9）：091201.

［2］ 唐王. 數據驅動的航空發動機余壽預測方法［D］. 南京：南京航空航天大學，2018.

［3］ 黃亮. 基于隨機過程的航空發動機剩余壽命預測及維修決策研究［D］. 南京：南京航空航天大學，2019.

［4］ 王鐘毓. 數據驅動的航空發動機異常檢測方法研究［D］. 南京：南京航空航天大學，2019.

［5］ ZIYA M S ，ENVER Y L，KARAKOC T H. Assessment of degradation effects for an aircraft engine considering exergy analysis［J］. Energy，2017，140：1417-1426.

［6］ DRING F，STAUDACHER S，KOCH C. Predicting the temporal progression of aircraft engine compressor performance deterioration due to particle deposition［C］//ASME Turbo Expo 2017： Turbomachinery Technical Conference and Exposition，Charlotte， North Carolina， USA： ASME，2017.

［7］ 林學森，李本威，趙勇，等. 渦軸發動機性能退化分析與診斷［J］. 燃氣渦輪試驗與研究，2015，28（6）：34-38.

［8］ 黃開明，LI Y G ，張偉，等. 某型渦軸發動機性能衰減與部件退化評估［J］. 航空動力學報，2015，30（11）：2673-2679.

［9］ ARETAKIS N，ROUMELIOTIS I，ALEXIOU A，et al. Turbofan engine health assessment from flight data［J］. Journal of Engineering for Gas Turbines and Power，2015，137（4）：041203.

［10］ ROUMELIOTIS I，ARETAKIS N，ALEXIOU A. Industrial gas turbine health and performance assessment with field data［J］. Journal of Engineering for Gas Turbines and Power，2017，139（5）：051202.

［11］ 徐田鎮. 航空發動機退化狀態參數估計與控制技術研究［D］. 南京：南京航空航天大學，2017.

［12］ 錢俊寧. 基于模型的航空發動機性能退化緩解控制研究［D］. 南京：南京航空航天大學，2015.

［13］ 李永進. 智能航空發動機性能優化控制技術研究［D］. 南京：南京航空航天大學，2018.

［14］ 楊思幸. 航空發動機性能恢復控制方法研究［D］. 南京：南京航空航天大學，2019.

［15］ 夏天乾，徐植桂，吳金棟，等. 基于動態逆的渦軸發動機自適應模型建模方法研究［J］. 機械制造與自動化，2022，51（5）：123-125，148.

［16］ 劉兆穎. 考慮發動機性能退化的渦輪葉尖間隙預估方法研究［D］. 南京：南京航空航天大學，2019.

收稿日期：20220725