高斯過程回歸在軸承健康狀態(tài)預測中的應用

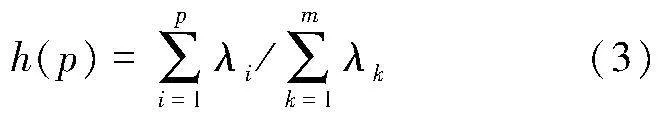
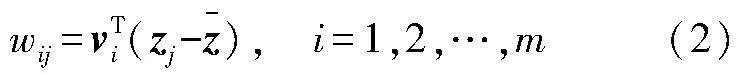
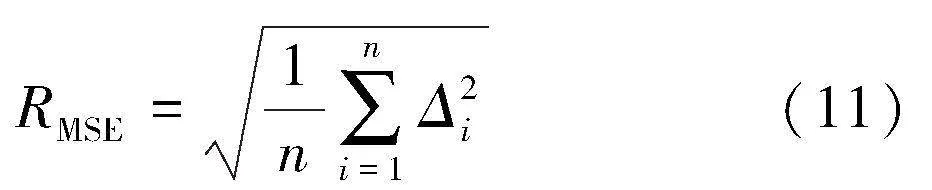
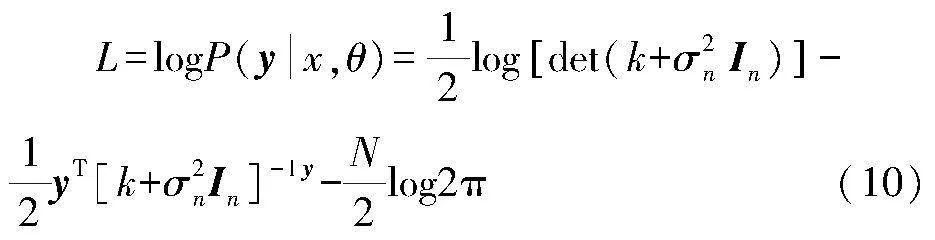
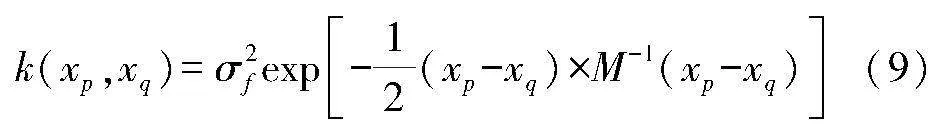
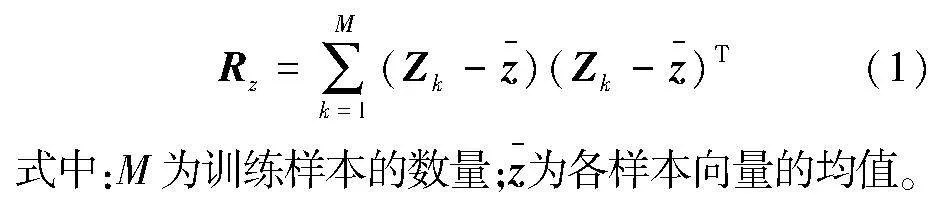
摘 要：軸承作為列車牽引電機的重要零部件，準確評估其后續(xù)健康狀態(tài)對列車的安全運行至關重要。基于軸承臺架試驗及實車數(shù)據(jù)，將主成分分析（PCA）和高斯過程回歸（GPR）應用于軸承的健康狀態(tài)評估及預測中。通過對試驗數(shù)據(jù)進行特征提取，獲得能夠表征軸承衰退規(guī)律的特征數(shù)據(jù)，應用PCA將提取的數(shù)據(jù)進行降維并建立軸承狀態(tài)評估數(shù)據(jù)，應用GPR對評估數(shù)據(jù)進行學習和預測。通過預測值與真實值的對比驗證，GPR可以實現(xiàn)軸承的健康狀態(tài)預測，并在低采樣率下保持了較高的準確率。

關鍵詞：軸承狀態(tài)預測；高斯過程回歸；主成分分析；牽引電機

中圖分類號：TH133.33；U279.3文獻標志碼：A文章編號：1671-5276（2024）03-0146-05

Application of Gaussian Process Regression in Prediction of Bearing Health

Abstract：Bearing is an important part of train traction motor and accurate evaluation of its subsequent health status is very important for train safe operation. Based on the bearing bench test and real vehicle data， principal component analysis （PCA） and Gaussian process regression （GPR） are applied to assese and predict bearing health status. Features are extracted from the experimental data， obtaining the characteristic data that can characterize the law of bearing degradation. PCA is used to reduce the dimension of extracted data and establish the bearing state assessment data， and GPR is applied to learn and predict the assessment data. Through the comparison of the predicted value and the true value， GPR can predict the health of bearing and maintain a high accuracy rate at a low sampling rate.

Keywords：bearing condition prediction; Gaussian process regression; principal component analysis; traction motor

0 引言

隨著大數(shù)據(jù)與機器學習算法的發(fā)展，越來越多的業(yè)主將產(chǎn)品的全壽命狀態(tài)監(jiān)測納入車輛的維保中［1］，同時對基于數(shù)據(jù)驅(qū)動的產(chǎn)品狀態(tài)評估與壽命預測提出了更高的需求。而軸承作為牽引電機的核心部件，其當前健康狀態(tài)及未來狀態(tài)預測對列車安全運行具有重要意義。目前在軌道交通領域應用較多的故障診斷系統(tǒng)來自于唐智公司基于共振解調(diào)技術開發(fā)的自診斷系統(tǒng)［2］。該系統(tǒng)具備軸承狀態(tài)判斷、故障部位報警的功能，但缺少業(yè)主更加關心的軸承狀態(tài)預測功能，無法為業(yè)主延長修程修制提供參考。本研究基于科技部國家重點研發(fā)計劃課題“高性能電機絕緣軸承運維監(jiān)測技術”項目需求，對目前牽引電機最常用的圓柱滾子軸承和深溝球軸承開展技術研究，通過PCA方法對軸承的特征指標進行融合并建立健康度指標；根據(jù)健康度指標評估軸承狀態(tài)并通過高斯過程回歸（GPR）算法完成軸承的健康狀態(tài)預測；使用臺架試驗數(shù)據(jù)及實車數(shù)據(jù)對該方法的準確性進行驗證。

1 軸承健康度指標建立

當軸承出現(xiàn)故障時，傳感器采集到的振動信號將出現(xiàn)一定的變化，該變化將同時反映到相關的特征指標中。通過提取振動信號的特征指標，根據(jù)軸承衰退規(guī)律選擇合適的特征指標，使用主成分分析（PCA）完成指標融合并根據(jù)軸承全壽命周期數(shù)據(jù)，建立合理的軸承健康指標。

1.1 振動信號特征指標提取

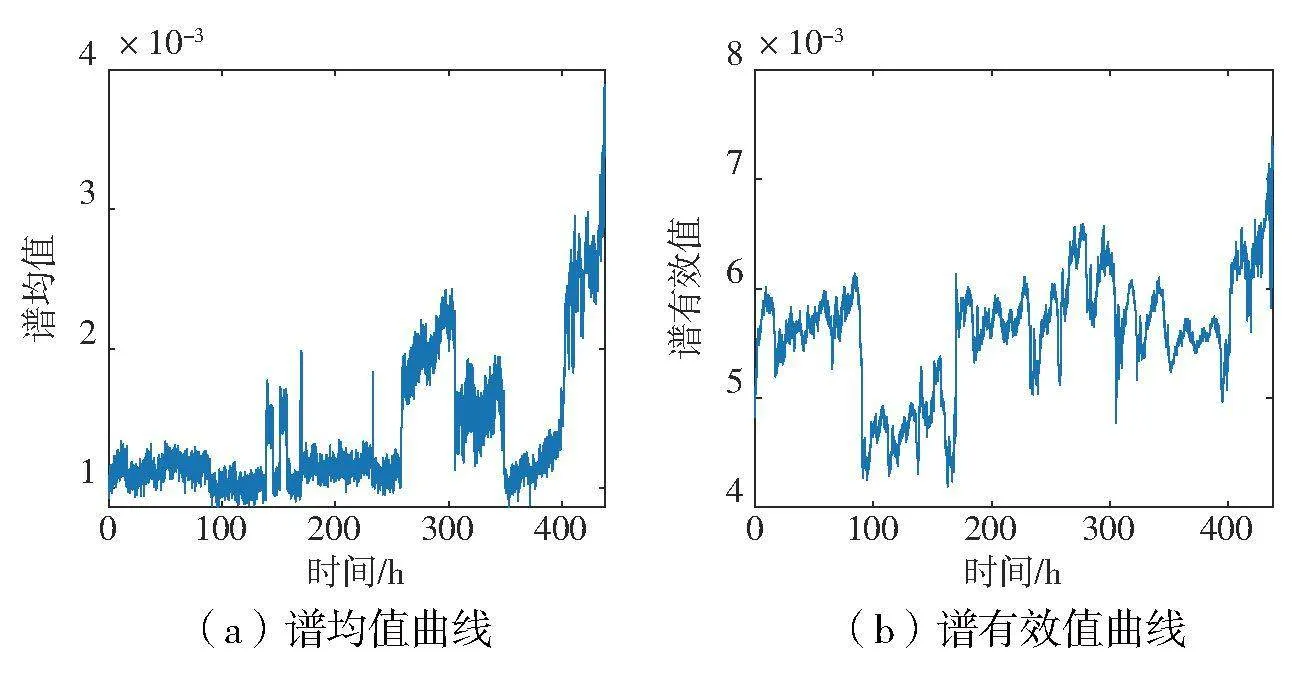
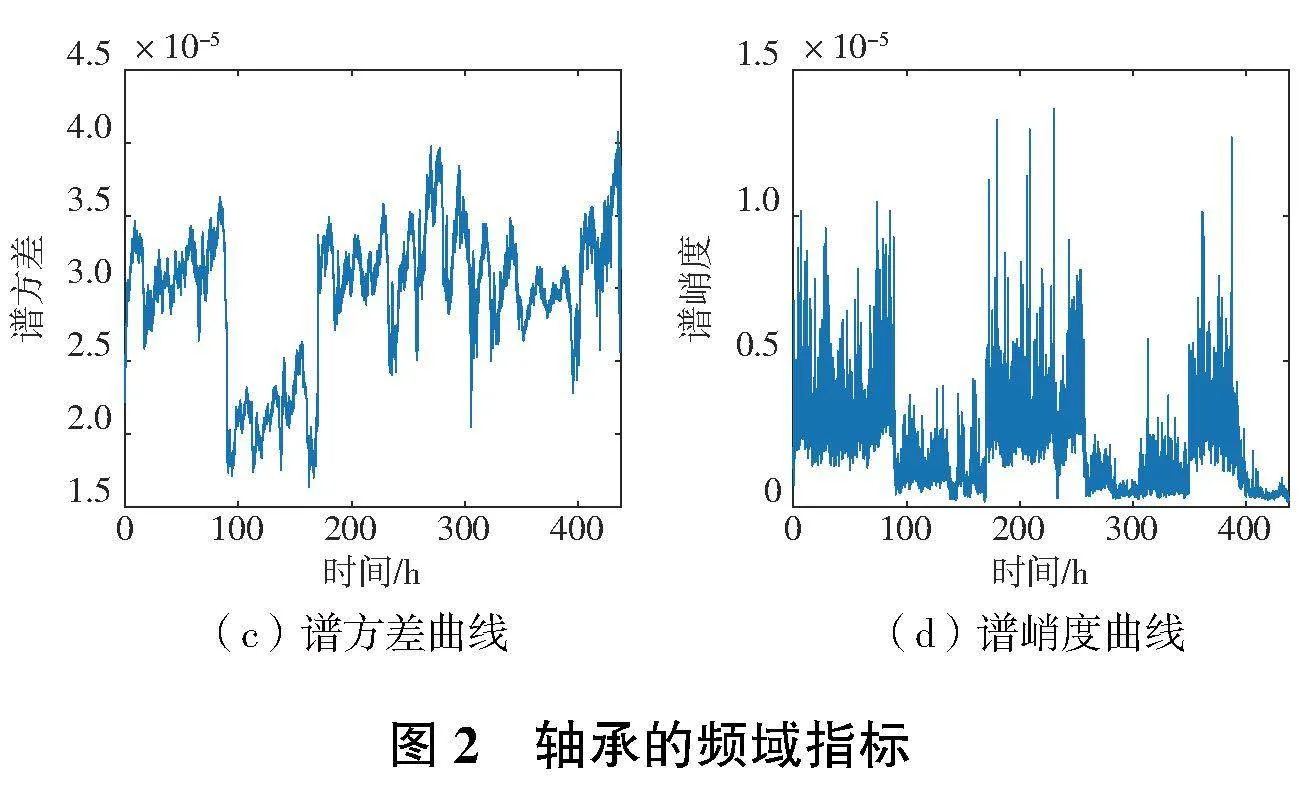
振動信號特征指標包含了時域指標、頻域指標及無量綱指標。時域指標中，有效值、方差的穩(wěn)定性較好，對沖擊不敏感；峰值、峰峰值、峭度及偏斜度對沖擊的敏感性較好。頻域指標中，譜均值和譜有效值用來衡量幅值的平均水平，穩(wěn)定性好；譜中心用來衡量頻譜中心的遷移情況；譜方差用來衡量幅值的波動性，部分特征指標如表1所示。

1.2 基于PCA的特征指標融合

通過對振動信號的特征提取，完成從低信息量到高信息量的轉變，但各個特征指標之間仍然存在冗余，過高的冗余度會降低模型精度，因此還需使用PCA對提取的特征信息做進一步融合。

PCA本質(zhì)是一種基于統(tǒng)計特征的多維正交線性變換，其基本流程如下［3］。

設軸承振動信號的特征向量矩陣為Z，其列向量Zk=（z1k，z2k，…，znk）T為n維特征向量，Zk的協(xié)方差矩陣為

求解Rz的全部特征值λi（i=1，2，…，m）和特征向量vi。將特征值λi按照從大到小的順序排列：λ1gt;λ2gt;…gt;λm，則對應的特征向量為vi（i=1，2，…，m）。樣本向量zi投影到特征向量vi得到該方向上對應的主成分為

特征向量所對應的特征值越大，它在重構時的貢獻也越大，前p個主成分的累計方差貢獻率為

1.3 軸承健康度指標建立

軸承的健康度指標是一種自比較的評估方法，該方法剔除了因裝配、外在環(huán)境對狀態(tài)評估的影響。以融合后指標的最大值與最小值作為參照，計算其相對距離并歸一化至［0，1］范圍內(nèi)，計算公式如下：

CV=1－d2/d1（4）

式中：CV為軸承健康度指標；d1為融合指標最大值與最小值之間的歐氏距離；d2為各時刻下融合指標與最小值之間的歐氏距離，均為無量綱指標。

2 軸承健康狀態(tài)預測

根據(jù)建立的軸承健康度指標，使用高斯回歸算法對軸承的健康度進行預測以評價未來一段時間內(nèi)的健康度能否滿足運行要求。

高斯過程回歸是指對輸入和輸出變量均為連續(xù)變量的情況進行預測［4］，給定訓練樣本集D=（xi，yi）i=1，2，…，n，其中，樣本集中的xi為輸入量且有xi∈Rd，yi為輸出量且有yi∈R。隨機高斯過程產(chǎn)生訓練樣本集，在輸入xi時對應隨機變量f（xi），考慮含噪聲εi產(chǎn)生的yi即為

yi=f（xi+εi）（5）

這里假設均值函數(shù)為0，εi為獨立同分布，則有εi～N（0，σ2n），在訓練集yi和測試點x*的y*的后驗分布是：

P（y*X，yi，x*）～N（u*，Σ*）（6）

u*=k（x*，X）k（X，X）+σ2nIn－1yi（7）

Σ*=k（x*，x*）－k（x*，X）×［k（X，X）+σ2nIn］－1k（X，x*）（8）

式中：u*為均值；Σ*為方差；In為n維單位矩陣；k（X，X）為對稱的協(xié)方差矩陣。

采用平方指數(shù)協(xié)方差函數(shù)作為高斯過程回歸的核函數(shù)：

θ=M，σ2n，σ2f為超參數(shù)，采用最大似然估計函數(shù)對其進行優(yōu)化［5］，公式如下：

式中y為輸出量yi的集合，即有y=y1，y2，…，yi。

針對超參數(shù)θ對似然函數(shù)L求導，最終計算得到最優(yōu)超參數(shù)M、σ2n、σ2f，代入式（7）、式（8）中得到預測的均值和方差，即為GPR模型的預測值及置信度。方差越小，則預測結果越好。

最后，采用方均根誤差（root mean square error，RMSE）來對算法的有效性進行評估［6］，公式如下：

式中：n為預測樣本數(shù)；Δi為各預測值與真實值之間的誤差。

3 臺架試驗驗證

3.1 數(shù)據(jù)來源及說明

本文采用在杭州某實驗中心進行的軸承衰退試驗數(shù)據(jù)進行驗證，軸承型號分別為NU214圓柱滾子軸承及6311深溝球軸承。試驗轉速2 500r/min，軸承承受徑向載荷28kN。試驗數(shù)采設備通過振動傳感器實時采集被試軸承的振動數(shù)據(jù)。采樣頻率25 600Hz，采樣間隔5min，單次采樣時長4s。

3.2 軸承健康指標建立

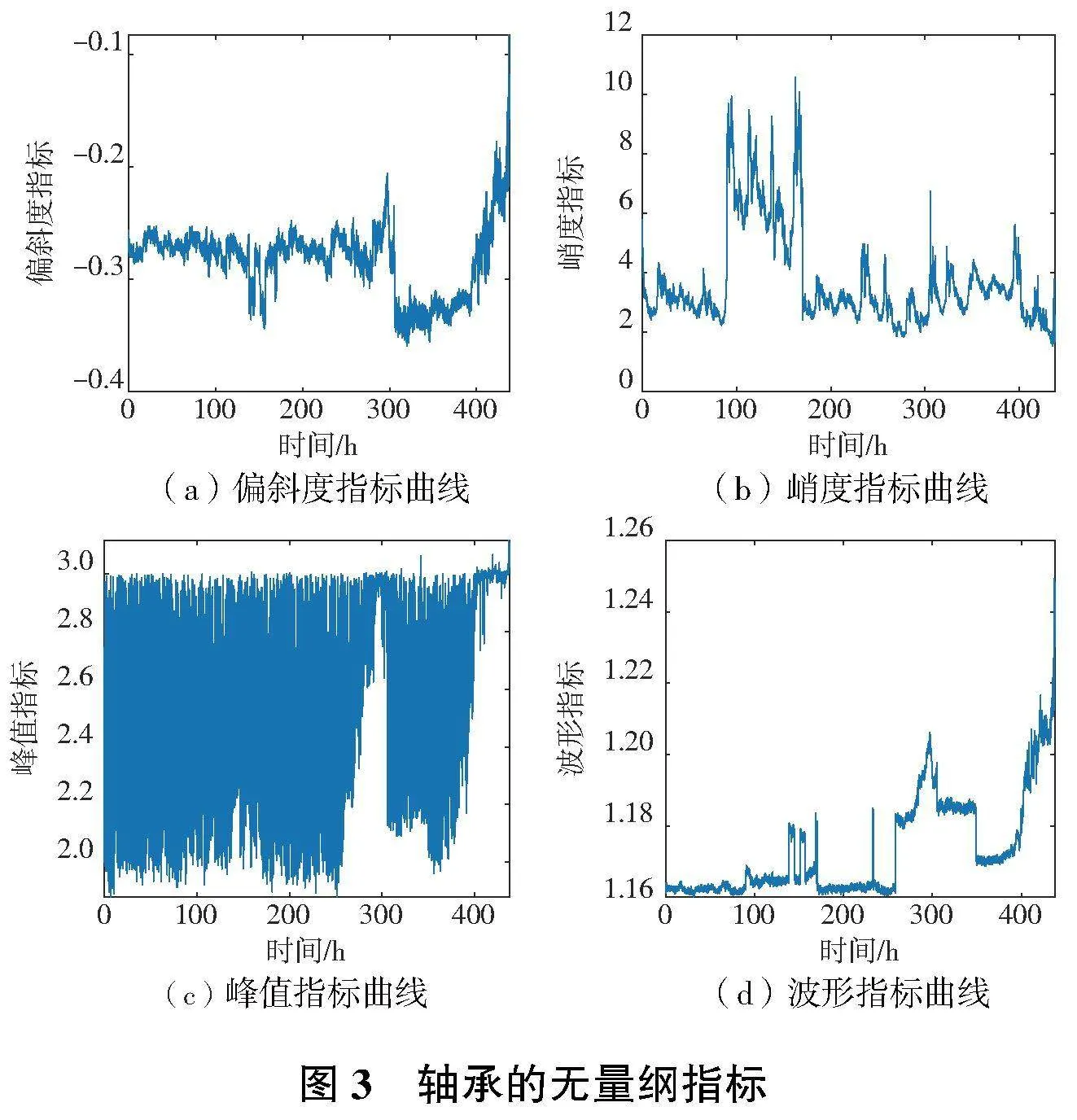
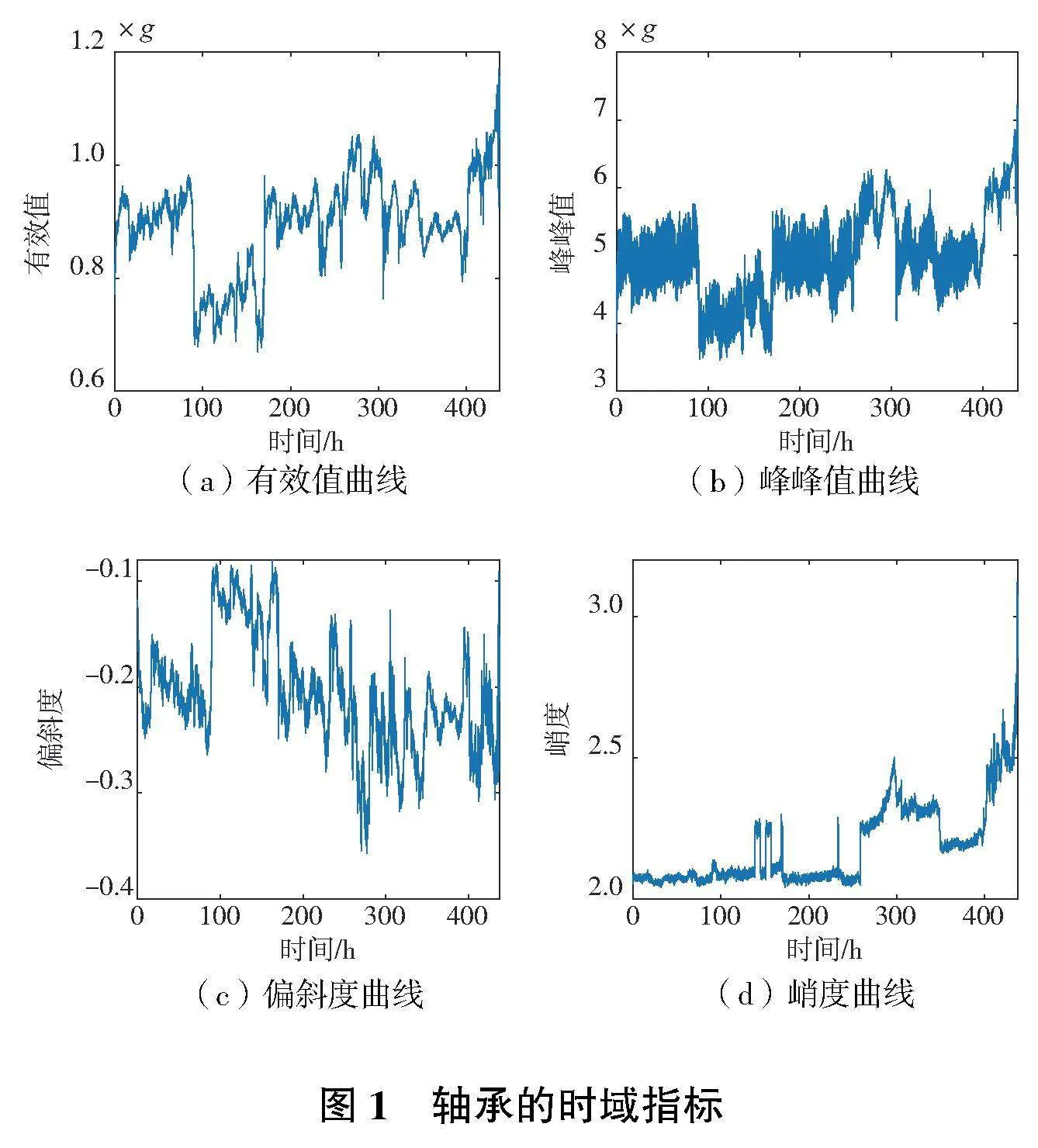
根據(jù)前文的方法對軸承的試驗數(shù)據(jù)進行特征指標的提取，部分結果如圖1—圖3所示。

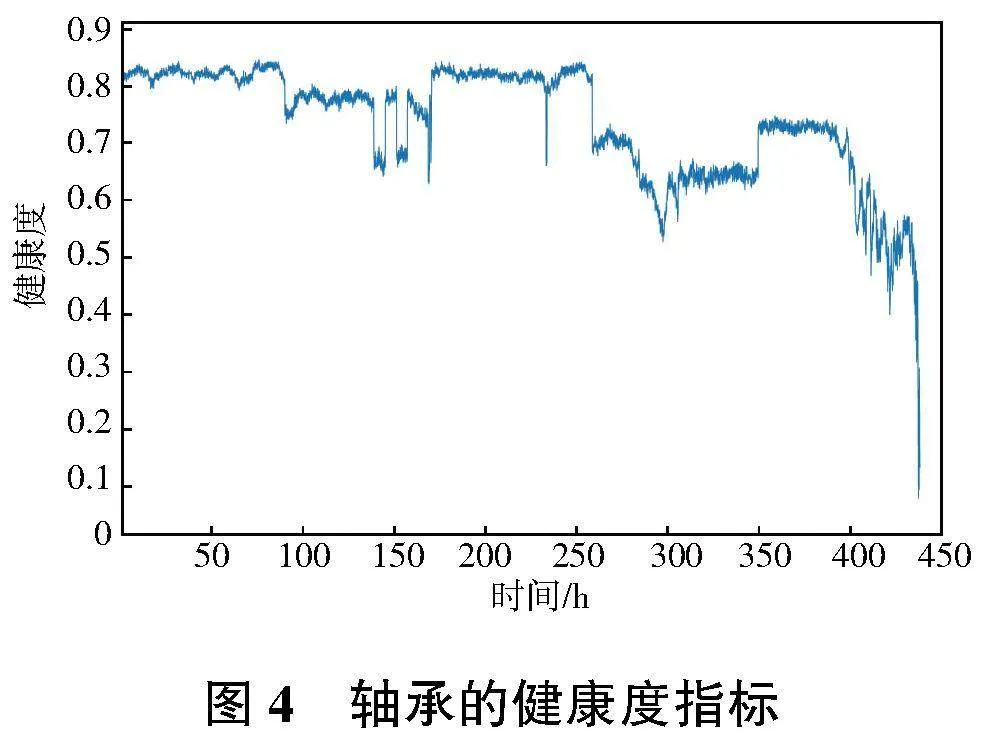
從圖1—圖3中可知，峰峰值及峰值指標的信息嘈雜，且未見明顯的衰退變化；偏斜度、譜峭度、峭度指標未見明顯衰退變化。將上述指標剔除后進行PCA特征融合，選擇貢獻率大于95%的數(shù)據(jù)建立軸承健康度指標，如圖4所示。

從圖4可以看出，通過軸承的健康度指標可以更加直觀地了解軸承狀態(tài)的衰退變化情況，在260h前后時間段內(nèi)有一個健康度指標降低的情況，因此可將260h前的階段定義為軸承正常運行階段，將260h～400h之間的階段定義為軸承的劣化階段。在劣化階段，軸承的健康度指標有一個先下降、后上升的過程。這是因為當軸承出現(xiàn)初始故障時，連續(xù)的運轉會導致軸承出現(xiàn)一定的剝落或裂紋，此時軸承的健康度隨之下降；隨著軸承的運行，損傷擴展到更廣的區(qū)域后，健康度會有一定程度的上升，這種現(xiàn)象被稱為“愈合”現(xiàn)象［7］。隨著軸承運行，軸承的健康度會在較短的時間內(nèi)快速衰退至0.2，達到完全失效狀態(tài)。

3.3 軸承健康狀態(tài)預測

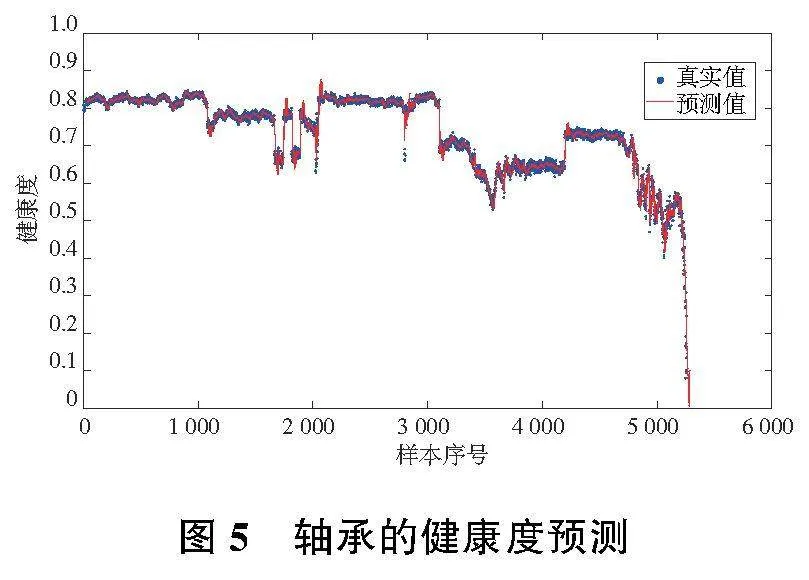
根據(jù)獲得的軸承健康度衰退變化規(guī)律，選擇平方指數(shù)協(xié)方差函數(shù)構建GPR模型，對軸承未來一段時間的健康度進行預測。以第41個點作為健康度預測的起點，保持建模數(shù)據(jù)間隔為5 min，預測未來30個點的健康度，預測結果如圖5所示。

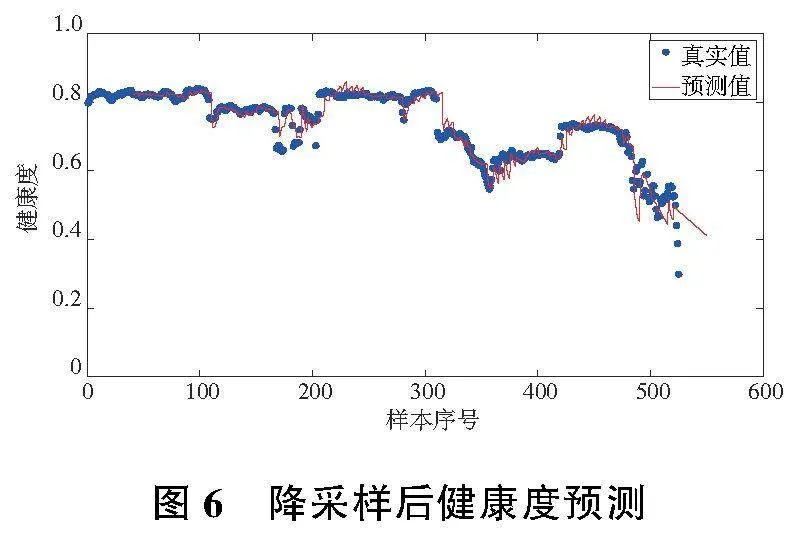
利用RMSE值對預測準確性進行計算，其中，全局預測的RMSE值為0.02，停機前最后30個點的RMSE值為0.32。原因為停機前軸承已進入失效狀態(tài)，短時間內(nèi)采樣點波動較大，軸承的健康度指標在小范圍內(nèi)出現(xiàn)一定的波動，造成預測值與真實值出現(xiàn)了一定的差異。為驗證模型在低采樣率下的準確性，對原始數(shù)據(jù)進行降采樣。將原先5min的采樣間隔提升為50min，軸承的健康度預測結果如圖6所示。

對降采樣后的預測結果求RMSE值，其全局預測RMSE值為0.03，停機前最后30個點的RMSE值為0.10。通過對比降采樣前后的RMSE值，停機前的預測準確性較降采樣之前有一定的提升，原因為降采樣在一定程度上剔除了軸承壽命最終階段較多的干擾數(shù)據(jù)，使預測結果與真實結果更為接近。

4 實車驗證

為進一步驗證該方法的準確性，使用某地鐵車輛車載PHM診斷單元的數(shù)據(jù)進行評估及預測。PHM診斷單元的采集機制為定轉速觸發(fā)采集，振動傳感器安裝于牽引電機的非傳動端，采樣頻率25 600Hz，采樣時長2s，采樣觸發(fā)轉速為（2 500±5%） r/min。

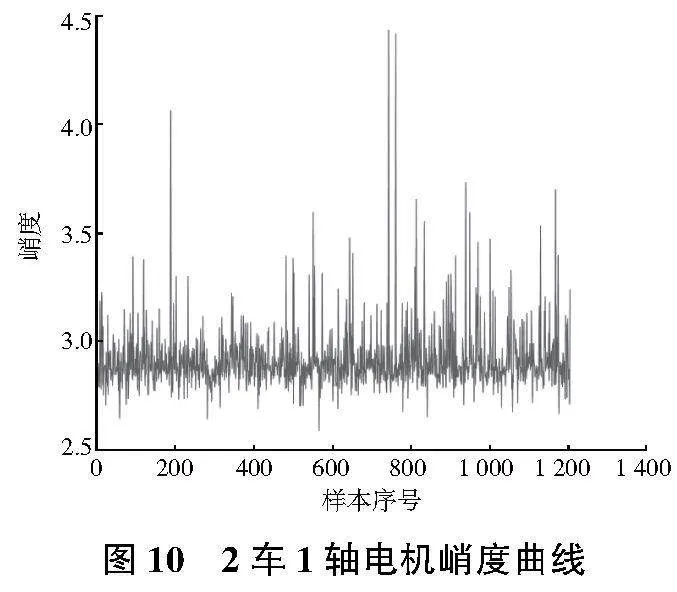
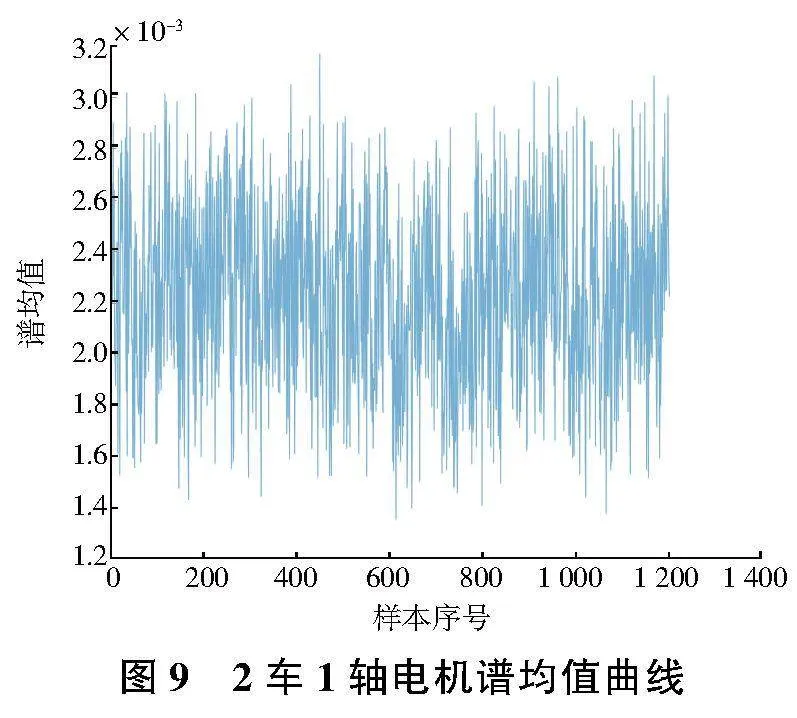
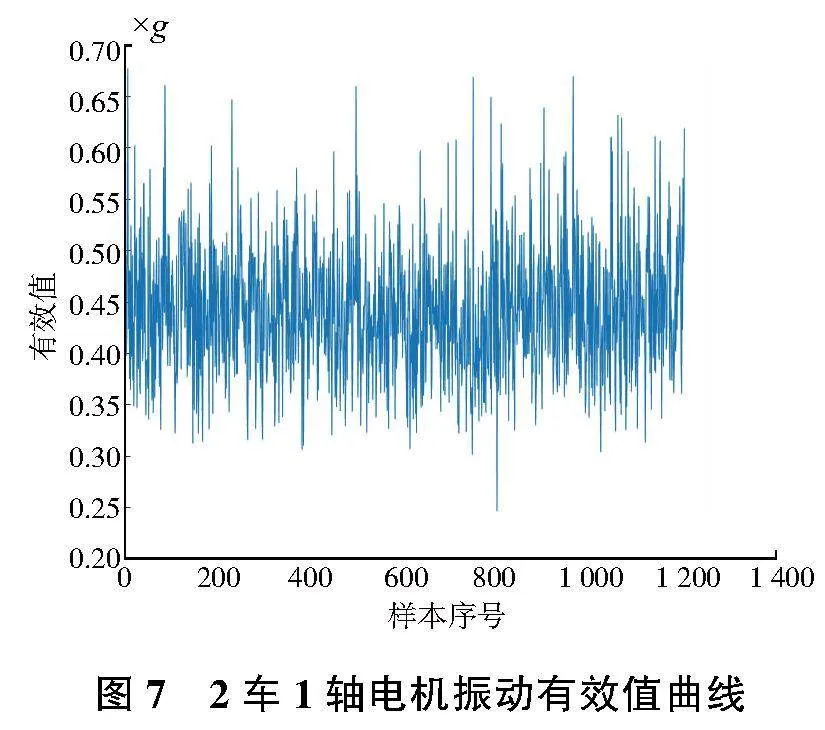
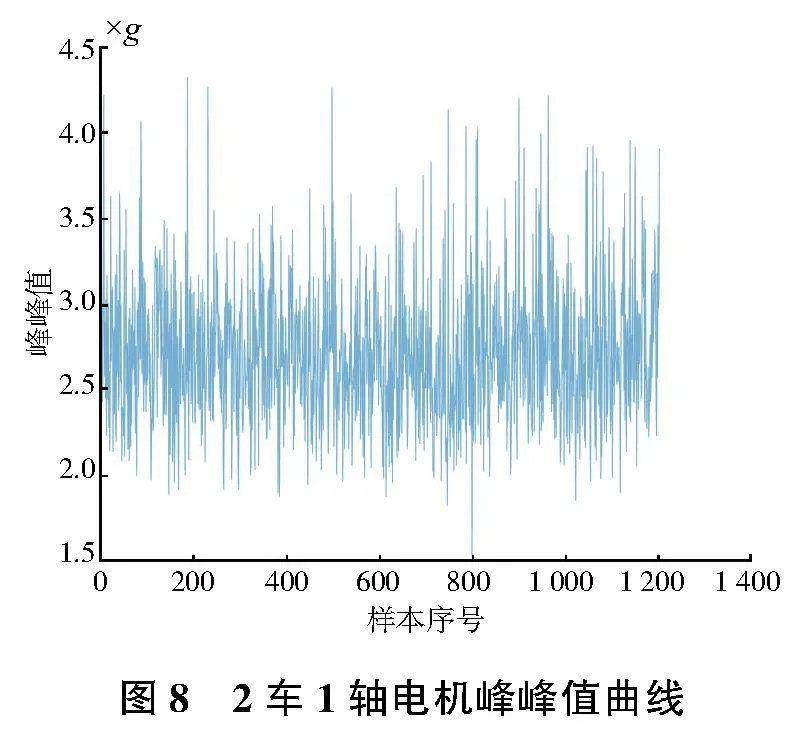
選取其中一臺牽引電機數(shù)據(jù)進行分析，部分特征指標如圖7—圖10所示。

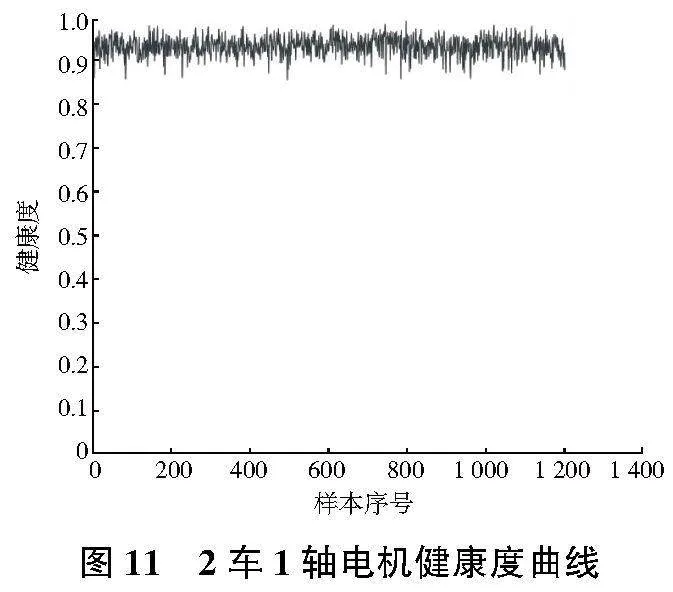
對特征指標進行PCA融合并建立的健康度曲線如圖11所示。

從圖11可以看出，雖然該電機軸承的振動有效值、峭度存在一定的變化，但其總體健康度維持在0.9以上。由于該車為全新運營車輛，運行里程較短，其健康度計算結果與電機軸承的實際狀態(tài)吻合。

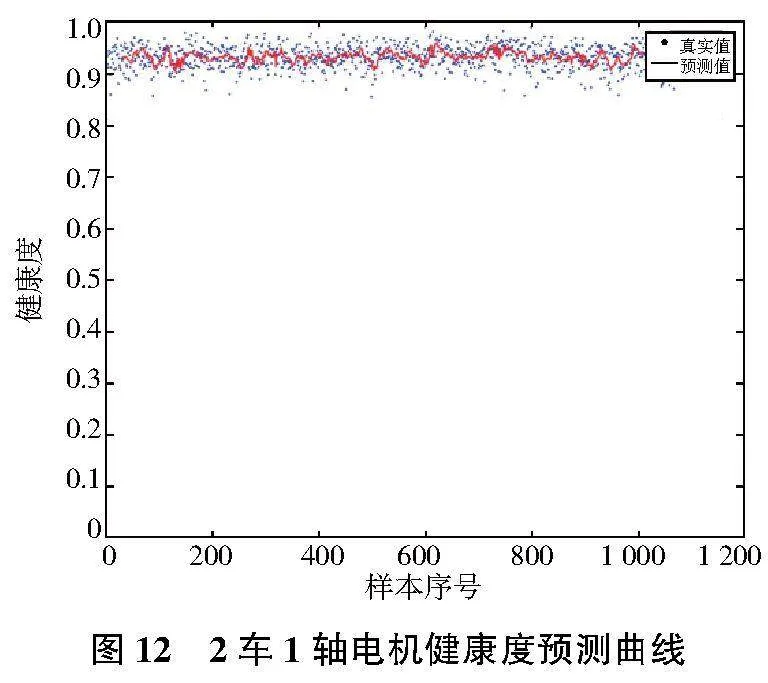
最后使用GPR模型對現(xiàn)有數(shù)據(jù)進行學習，并預測未來一段時間內(nèi)的軸承健康度變化情況，同時與真實數(shù)據(jù)進行對比，其預測健康度變化如圖12所示。

根據(jù)RMSE計算結果，2車1軸電機的全局RMSE值及最后30個預測點的RMSE值均為0.07，這表明實車驗證的準確性已接近臺架試驗驗證的準確性，具備進一步推廣的基礎條件。

5 結語

針對現(xiàn)階段只能對軸承是否存在故障進行判斷、無法預測軸承后續(xù)運行狀態(tài)的問題，通過使用PCA技術對軸承振動的時頻域指標進行融合并建立一個可以表征軸承衰退性能的健康度指標，進而利用GPR技術完成軸承的健康狀態(tài)預測研究，再根據(jù)RMSE值完成預測準確性評估。試驗結果表明，使用健康度評估方法能夠較為準確地評估軸承狀態(tài)，通過GPR技術預測臺架試驗軸承健康度的全局RMSE值為0.02，預測實車牽引電機軸承健康度的全局RMSE值為0.07，驗證了所提方法的可行性和準確性，為后續(xù)進一步開展基于軸承健康度的狀態(tài)評估及壽命預測奠定了理論基礎。

參考文獻：

［1］ 曹勇，張玉文，龔艷. 基于大數(shù)據(jù)和云計算的車輛智能運維模式［J］. 城市軌道交通研究，2020，23（4）：69-73.

［2］ 許艷華，黃貴發(fā)，唐德堯. 城軌交通車輛走行部故障自動診斷技術應用［J］. 都市快軌交通，2012，25（5）：131-135.

［3］ 劉永斌，何清波，孔凡讓，等. 基于PCA和SVM的內(nèi)燃機故障診斷［J］. 振動、測試與診斷，2012，32（2）：250-255，342.

［4］ 王巍. 基于稀疏高斯過程回歸的鋰電池剩余壽命預測［D］. 北京：北京交通大學，2018.

［5］ RASMUSSEN C E，WILLIAMS C K I. Gaussian processes for machine learning［M］. Cambridge，Mass. ：MIT Press，2006.

［6］ 魏孟，李嘉波，葉敏，等. 基于高斯混合回歸的鋰離子電池SOC估計［J］. 儲能科學與技術，2020，9（3）：958-963.

［7］ WILLIAMS T，RIBADENEIRA X，BILLINGTON S，et al. Rolling element bearing diagnostics in Run-to-failure lifetime testing［J］. Mechanical Systems and Signal Processing，2001，15（5）：979-993.