Stewart型并聯機器人的奇異對其運動精度的影響













摘 要:以9-3 Stewart型并聯機器人為研究對象,分析其在機構接近奇異位形時動平臺運動精度的情況。通過計算并聯機器人速度Jacobian矩陣的行列式得到奇異點的坐標。通過虛擬樣機實驗,得到動平臺參考點位置反解和正解計算的相對誤差。用轉動Jacobian矩陣條件數的倒數來度量機構接近奇異的程度,并分析該程度與上述相對誤差之間的映射關系。研究結果表明:當指標值大于7.027×10-5時,正、反解的相對誤差可忽略不計,這為奇異規避、路徑規劃等后續工作提供了理論參考。
關鍵詞:并聯機器人;正解;反解;運動精度;奇異位形;Jacobian矩陣
中圖分類號:TH122; TP242文獻標志碼:A文章編號:1671-5276(2024)03-0195-04
Effect of Singularity on Motion Accuracy of Stewart Parallel Robot
Abstract:Taking 9-3 Stewart parallel robot as the research object, analyzes the motion accuracy of moving platform when mechanism is close to singular configuration. The determinant of velocity Jacobian matrix of the parallel robot is calculated to abtain the coordinates of singular points. The virtual prototype experiment is conducted to gain the relative error of the inverse solution and positive solution of the reference point of the moving platform. The reciprocal of the condition number of the rotating Jacobian matrix is used to measure the degree of the mechanism approaching singularity, and the mapping relationship between this degree and the above relative error is analyzed. The results show that when the index value is greater than 7.027×10-5, the relative error of the positive and negative solutions can be ignored, which provides a theoretical reference for the follow-up work such as singularity avoidance and path planning.
Keywords:parallel robot; positive solution; inverse solution; motion accuracy; singular configuration; Jacobian matrix
0 引言
機器人可以從構型上劃分成串聯機器人和并聯機器人兩種。與傳統的串聯機器人相比,并聯機器人具有輸出精度高、承載能力強、累積誤差小、結構緊湊等優點[1]。所以,并聯機器人被廣泛地應用于需要高精度的工業生產中,比如軍事領域中的潛艇、坦克駕駛運動模擬器;食品、電子、化工、包裝等行業的分揀、搬運、裝箱等。在現有的6自由度并聯機器人中,最成功和最具代表性的是Gough-Stewart平臺,其移動平臺是通過6個結構相同的支鏈連接到固定底座,形成閉環架構[2]。由于人們追求并聯機構盡可能地滿足更多需求,具有更好的性能,Stewart型并聯機器人應運而生。對于Stewart型并聯機器人來說,安裝在動平臺上的球副在空間上是任意排列的,不一定是共面的,而且支鏈的數量也允許多于6個[3]。鑒于這些幾何特征,Stewart型并聯機器人在工業上的應用將比傳統的Gough-Stewart平臺更廣泛。
國內外關于并聯機器人的研究主要集中在機構學、運動學、動力學和控制策略等方面,其中奇異位形是衡量并聯機器人運動性能的一個重要指標[4]。奇異位形是當機構運動進入某種臨界狀態時所具有的特定位形,是并聯機器人的一項重要運動學特性。在這種臨界狀態下,機構的實際自由度數不再與其理論自由度數相等[5]。自由度為6的并聯機構的奇點軌跡是一個6維超曲面,無法用圖形表示。當奇異點出現在工作空間內部或它的邊界時,一個并聯機構就不能被完全控制,而且它的性能會變得較差,比如靜剛度會顯著降低。在實際應用中,并聯機構會被限制在一個無奇異點的子空間中。因此,對并聯機構的奇異性進行分析具有重要意義。
GOSSELIN等[6]首先根據末端執行器和驅動器的速度關系式提出了3種類型的奇異位形。HAO、MERLET和COLLINS等[7-9]分別采用線叢原理和Clifford代數對奇異位形存在的條件進行了研究。李虹等[10]通過3-RRP平面并聯機構的運動學方程求解機構Jacobian矩陣,分析該機構的奇異位形。仇鑫等[11]以一種可重構Stewart型并聯機器人為研究對象,對其奇異特性進行了理論分析。孫占朋等[12]研究自由漂浮空間機器人回避奇異的路徑規劃問題,使得空間機器人在運行過程中能夠有效地解決反解問題。
為進一步減少或消除奇異性的影響、擴大并聯機器人的實用化和產品化規模,本文以9-3(其中9、3分別表示靜平臺、動平臺上球副的數量)Stewart型并聯機器人為研究對象,分析其奇異特性對運動精度的影響,研究結果將對后續奇異位形的規避以及路徑規劃等工作具有指導意義。
1 奇異點計算及虛擬樣機實驗
1.1 計算奇異點
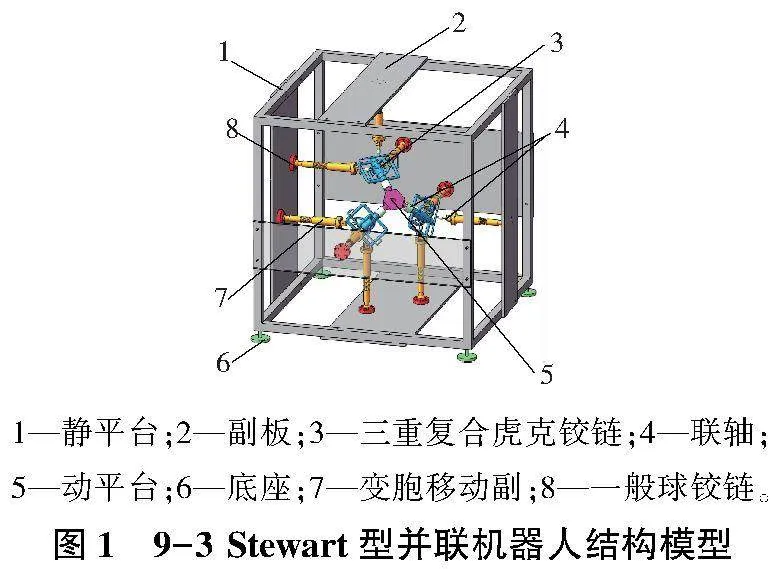
9-3 Stewart型并聯機器人由1個動平臺、1個靜平臺以及9條具有完全相同結構的支鏈組成。其中,每條支鏈都是由1個一般球面副、1個復合虎克鉸鏈和1個移動副組成。
其結構模型和機構簡圖分別如圖1、圖2所示。當其Jacobian矩陣的行列式等于0時,機構發生奇異。
在動平臺上任選一點P為參考點,基于速度基點法,每條支鏈的速度可以表示為
vbj=vp+ωp×(boj-po) (j=1,2,3)(1)
式中:vp和ωp分別表示點P的線速度和動平臺的角速度;boj、po分別表示動平臺上的點bj和點P的位置矢量。
將上式的等號兩端同時點乘支鏈的單位方向向量,整理后可得第i條支鏈的速度為
ii=vbj·hi=hTi·vp+[(boj-po)·hi]×ωp(2)
式中hi表示支鏈i的單位方向向量。
根據移動副的工作模式,9-3 Stewart并聯機器人可以重構為 3-2-1構型和2-2-2構型,前、中、后3個數字各代表一條混合單開鏈支路中驅動副的個數。可以得到2-2-2和3-2-1構型并聯機構的速度Jacobian矩陣J1、J2分別為:
基于式(3)和式(4),計算速度Jacobian矩陣行列式為0時P點的坐標,所求出的坐標即為相應構型的奇異點的坐標。由此可得到:
1) 當9-3 Stewart型并聯機器人為2-2-2構型時所求得的奇異點坐標為
2) 當9-3 Stewart型并聯機器人為3-2-1構型時所求得的奇異點坐標為
考慮到速度Jacobian矩陣量綱不統一會導致其條件數無意義,令J-1=G,則
式中:G1為移動Jacobian矩陣;G2為轉動Jacobian矩陣。G1與參考點的選取有關,而G2與參考點的選取無關,本文僅考慮后者。
1.2 虛擬樣機實驗
在ADAMS軟件中建立機器人的虛擬樣機并進行運動學仿真,流程圖如圖3所示。
第一步:在模型上創建點,其坐標為前文計算出的6個奇異點坐標,如圖4所示。
第二步:驅動動平臺,確定移動副驅動量。
1)選定P點為動平臺參考點,建立該點到奇異點的移動副。
2)創建P點上的一般點驅動。
3)將時間設置成1s,步數設置成500步,進行模擬仿真。整個仿真的過程就是動平臺從初始位置向奇異點方向運動再返回的過程。
4)仿真結束后,將此時P點的坐標導出。
5)基于B1—B9點的坐標和b1、b2、b3點的坐標,確定移動副驅動量。
第三步:驅動支鏈。
①在ADAMS軟件中導入2-2-2驅動模式和3-2-1驅動模式下移動副隨時間變化的數據。
②在驅動支鏈上建立平移驅動。
③設定仿真時間為1s,步數為500步。
④導出仿真停止時P點的坐標,作為動平臺參考點的仿真值數據。
2 數據處理與分析
2.1 數據的處理
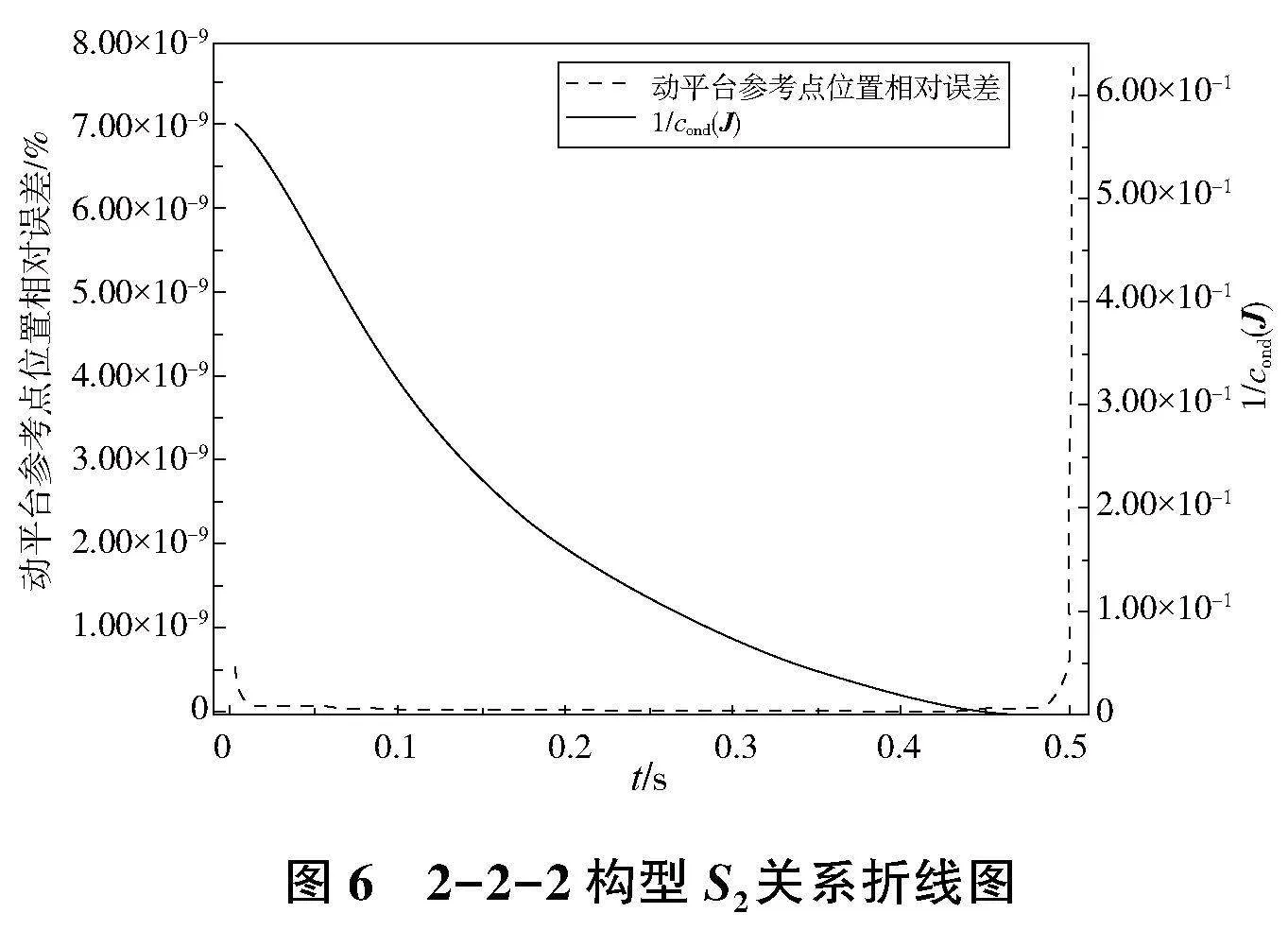
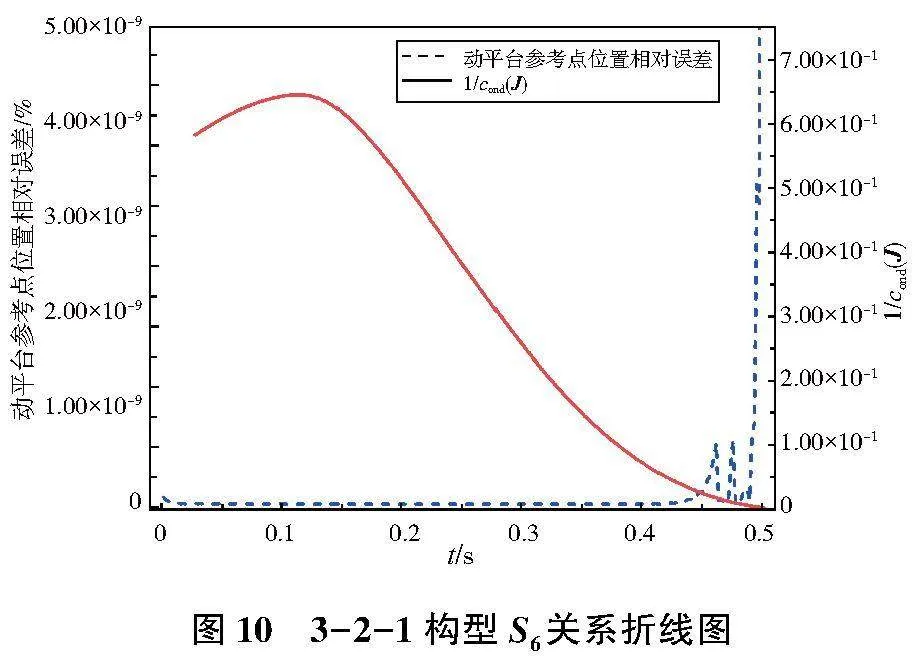
計算P點準確值和仿真值3個分量的相對誤差并求平均值,用轉動Jacobian矩陣條件數的倒數來度量機構接近奇異的程度,得到的數據曲線如圖5—圖10所示。
2.2 數據的分析
以3-2-1構型時的S6點為例,分析0.42s~0.50s之間動平臺參考點位置相對誤差與轉動Jacobian矩陣條件數倒數之間的關系,如圖11所示。
結果顯示,隨著動平臺不斷向奇異點運動,轉動Jacobian條件數的倒數不斷趨近于0,在該值約等于7.027×10-5時,動平臺參考點位置相對誤差發生突變。
3 結語
利用ADAMS軟件仿真了9-3 Stewart型并聯機器人在2-2-2構型和3-2-1構型時的情況,分析了動平臺接近奇異位形時的運動精度。
本文從運動傳遞性能的角度,通過虛擬樣機實驗研究了機器人Jacobian矩陣條件數的臨界值,而并沒有考慮機構的力傳遞性能。接下來主要考慮兩個方面工作:
1)探究并聯機器人的力傳遞性能與奇異性能之間的關聯;
2)通過實物樣機實驗,驗證并聯機器人的奇異性能對運動/力傳遞性能的影響規律。
參考文獻:
[1] ENFERADI J,NIKROOZ R. The performance indices optimization of a symmetrical fully spherical parallel mechanism for dimensional synthesis[J]. Journal of Intelligent amp; Robotic Systems,2018,90(3):305-321.
[2] 相鐵武. Stewart并聯機器人仿真系統實現分析[J]. 中國設備工程,2020(6):32-33.
[3] OU J J,XI F F,SHEN H P,et al. A novel stewart-type parallel mechanism with topological reconfiguration:design,kinematics and stiffness evaluation[J]. Mechanism and Machine Theory,2021,162:104329.
[4] 童身亮. 發動機輕量化途徑及工藝創新探究[J]. 內燃機與配件,2021(5):33-34.
[5] 王國華,寧玉浩,陳笑天,等. 鍛鋼活塞有限元分析及優化[J]. 內燃機,2019(6):40-42.
[6] 宋樹峰,薛冬新,王洪峰,等. 某柴油機機體靜強度有限元分析[J]. 內燃機與動力裝置,2018,35(2):47-51.
[7] 江海洋,孫明月,吳銘方,等. 7075鋁合金熱變形連接接頭的組織與性能[J]. 金屬熱處理,2020,45(2):46-50.
[8] 李貴旺. 海上平臺往復式活塞壓縮機故障分析及輕量化改造[J]. 天津科技,2020,47(4):55-58.
[9] 胡振,喬信起,王渠東,等. 發動機活塞輕量化的研究進展[J]. 小型內燃機與摩托車,2013(6):76-81.
[10] 牛飛. 結構拓撲優化設計若干問題的建模、求解及解讀[D]. 大連:大連理工大學,2013.

