磁懸浮軸承系統辨識與魯棒控制

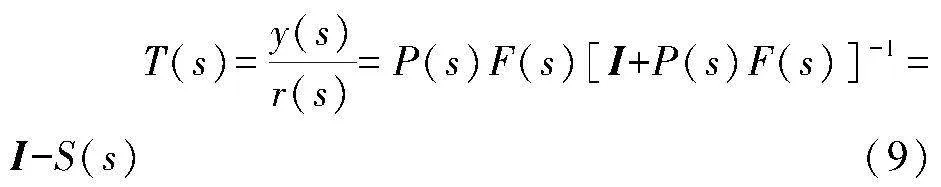
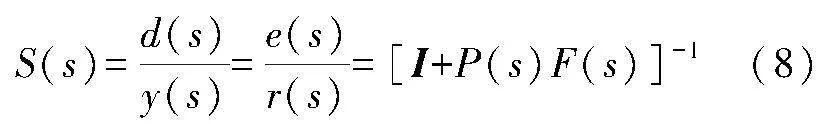
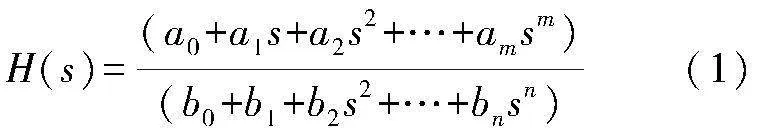
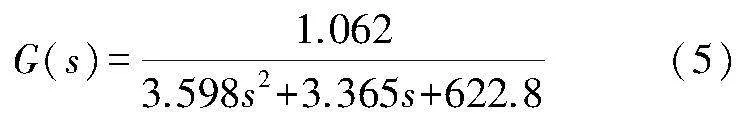
摘 要：為解決傳統魯棒控制器設計中存在的磁懸浮軸承被控模型建模復雜且難以準確建模的問題，運用正交多項式擬合方法，對模態實驗測得轉子的剛體模態及彎曲模態頻響數據進行系統辨識，建立磁懸浮軸承轉子系統被控模型；基于系統辨識所建立的磁懸浮軸承被控模型進行H∞魯棒控制器設計。實驗結果證明：基于系統辨識模型的魯棒控制器能夠實現轉子的穩定懸浮及對轉子剛體模態的控制。

關鍵詞：磁懸浮軸承；魯棒控制；系統辨識

中圖分類號：TH133.3文獻標志碼：A文章編號：1671-5276（2024）03-0204-05

System Identification and Robust Control of Magnetic Suspension Bearing

Abstract：Regarding the complexity and dificulty in accurate modeling of magnetic suspension bearing rotor in the design of traditional robust controllers， the orthogonal polynomial fitting method is applied to measure the rigid body mode and systematically identify frequency response data of bending mode of the rotor through the modal experiment， and the controlled model of the magnetic suspension bearing rotor system is established. An H∞ robust controller is designed based on the controlled model of the maglev bearing established by system identification. The experimental results prove that the robust controller based on the system identification model can realize the stable suspension of the rotor and control the rigid body mode of the rotor.

Keywords：magnetic suspension bearing; robust control; system identification

0 引言

磁懸浮軸承主要依靠電磁力對轉子進行控制，使轉子懸浮在指定位置。磁懸浮軸承的振動控制一直是研究的核心問題之一。魯棒控制器由于其抗干擾能力強，能夠保證系統參數在一定范圍內攝動均能實現穩定等優勢，已經在磁懸浮軸承轉子系統控制中得到了廣泛的應用。

目前關于磁懸浮軸承魯棒控制器已經做了一定研究，MUSHI等［1］針對壓縮器中轉子所受氣動載荷的影響，設計了μ綜合魯棒控制器，有效抑制了系統中存在的擾動。RAN等［2］分別設計了H∞及μ綜合魯棒控制器，實現了磁懸浮軸承系統的過臨界。

魯棒控制器的設計依賴于被控模型的建立。由于磁懸浮軸承系統復雜，很難快速地建立精準被控模型。系統辨識為被控模型的快速搭建提供了可能性，同時辨識的模型在頻域具備更好的擬合性，因此可以基于系統辨識的被控模型建模快速設計魯棒控制器。VAZQUEZ等［3］對磁懸浮軸承轉子模型進行了系統辨識；孫喆等［4］通過磁懸浮軸承掃頻激勵，提出了一種柔性轉子模型測試與辨識的方法。

本文采用正交多項式擬合法對磁懸浮軸承轉子系統進行頻響辨識，選取合適的頻段辨識系統模態參數，從而得到所需的被控模型；基于所辨識的被控模型進行H∞魯棒控制器設計，最終通過實驗驗證了所設計控制器的有效性。

1 系統模型辨識

1.1 正交多項式擬合原理

對于圖1所示的多自由度系統，其節點與節點之間存在一定的頻響關系［5］，可以寫成如下有理分式多項式。

式中：分母階次n=2N；分子階次m=n-2。此時分子分母多項式可以分別表達為

將式（1）分子、分母同除bn，在擬合過程中引入負頻率［6］，滿足H（jω－i）=H（－jωi）=H*（jωi）。

將式（1）左右同乘分母多項式并基于最小二乘法將其線性化，得到擬合方程為

式中：X=-Re（PHQ）; Y=0.5（PHP+PTP*）; Z=0.5（QHQ+QTQ*）; G=Re（PHW）; F=Re（QHW）; C=（a0，a1，…，am）T; D=（b0，b1，…，bn-1）T;

將冪基多項式轉化為Forsythe復正交多項式，其表達式形式如下：

1.2 轉子系統擬合

基于上文所述的有理多項式擬合方法［7］，本節開展磁懸浮軸承轉子系統的擬合。通過模態敲擊實驗可以得到轉子所需兩節點之間的頻響數據，基于此類數據，進一步開展被控模型辨識，并以此作為控制器設計的基礎。

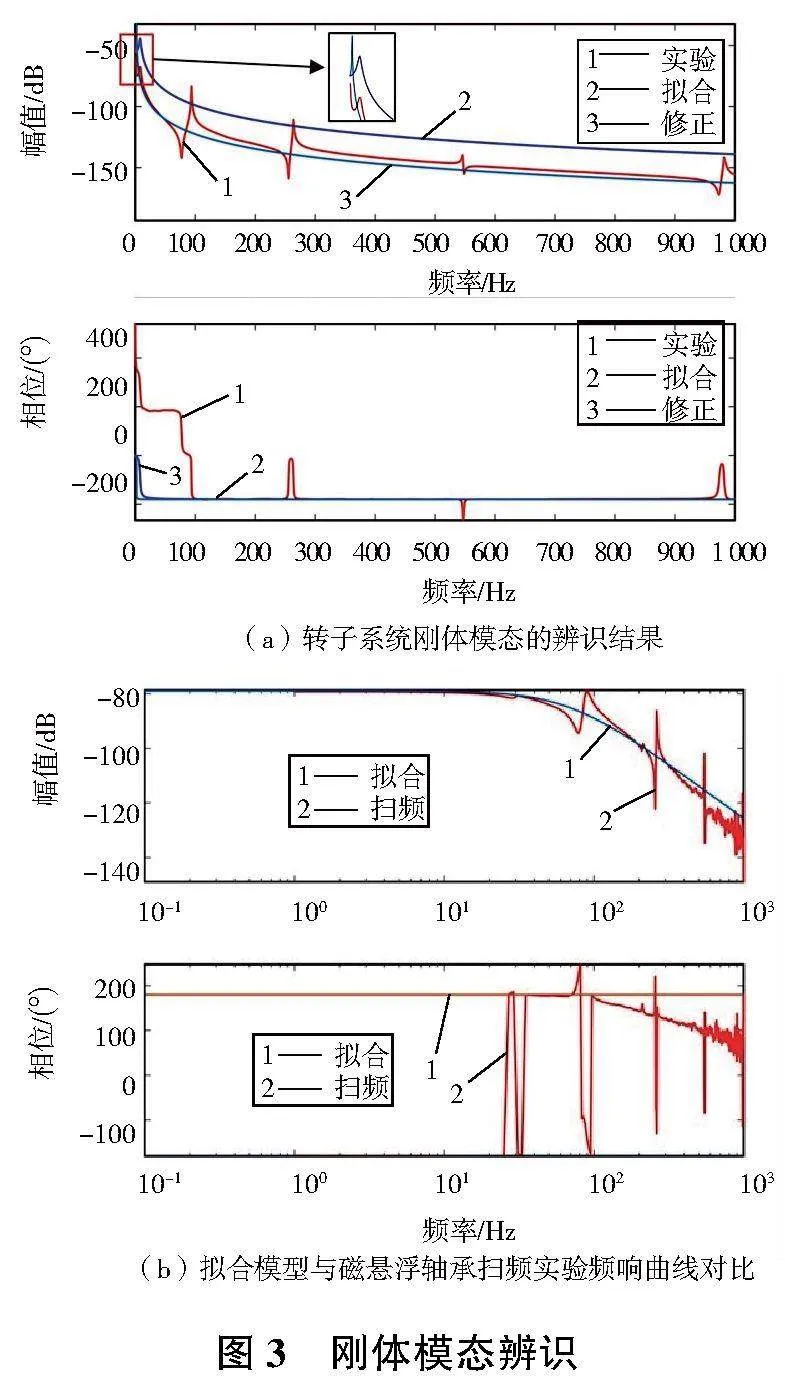
圖2為轉子系統測得位移頻響數據，擬合一階模態需采用二階傳遞函數。在控制器被控模型設計中，首先需要擬合的為轉子的剛體模態，此時選取頻段0～30Hz進行模型擬合，其擬合曲線如圖3所示。

通過圖3（a）局部放大可以看出，由于模態敲擊實驗中很難做到自由—自由態，因此存在一定的支承剛度，剛體模態頻率不為0。此時由于擬合曲線僅由剛體模態決定，所擬合的頻響模型與實驗頻響曲線幅值存在一定差距，但總體趨勢保持一致。為了保證辨識模型的準確，對此模型進行修正，使其剛體模態頻率接近0。圖中3曲線為修正后模型的頻響曲線，其傳遞函數如下：

從式（5）可得剛體模態頻率為2Hz，從圖3中可以看出其擬合性得到了明顯的改善。將所辨識的轉子模型代入磁懸浮軸承轉子系統模型中，由圖3（b）可以看出，辨識被控模型曲線與掃頻實驗頻響曲線具有較好的擬合性。

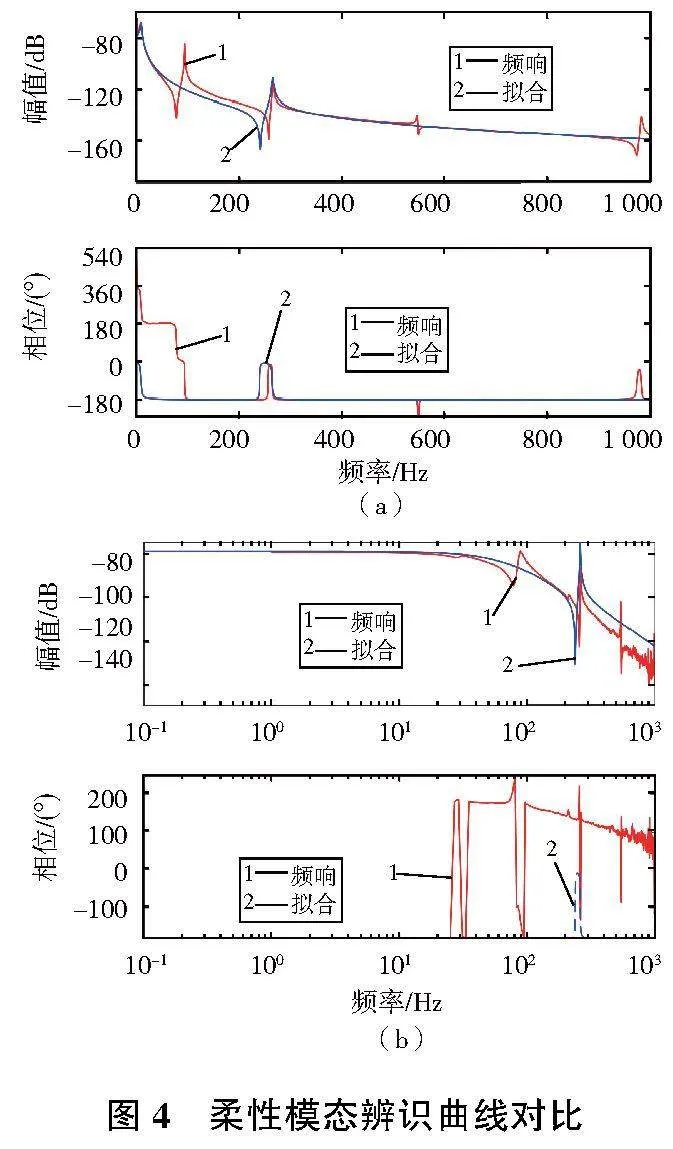
為了驗證系統擬合方法對磁懸浮軸承轉子系統彎曲模態辨識的有效性，選取3～30Hz、246～400Hz，辨識轉子的剛體模態及二階彎曲模態，選用四階傳遞函數進行擬合，其擬合傳遞函數如下：

柔性模態辨識曲線對比如圖4所示，此時辨識被控模型曲線與實驗測得頻響函數擬合性較好。傳遞函數由剛體模態及二階彎曲模態疊加而成，因此未出現前文所述的剛體模態頻率不為0導致的擬合不準確問題。通過上述擬合實驗驗證了系統擬合的可行性與有效性。

2 控制器設計與仿真

2.1 魯棒控制器理論

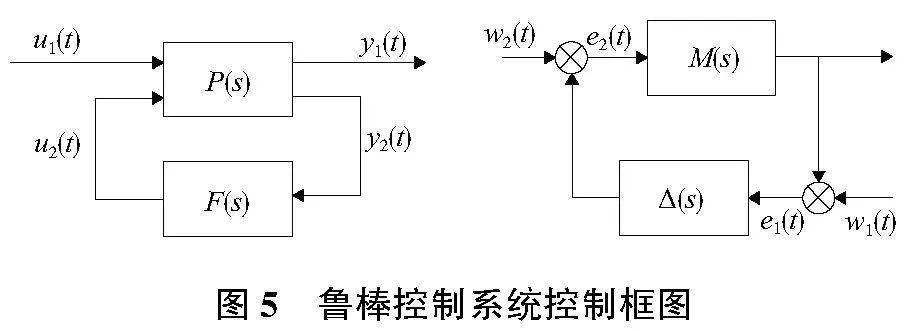
魯棒控制系統的結構如圖5所示，P（s）為被控對象，F（s）為控制器模型；e1（t）、e2（t）為系統傳遞中的中間變量。輸入u1（t）到輸出y1（t）的傳遞函數可以表示為Ty1u1。小增益定理如圖所示［8］，M（s）為線性控制系統，Δ（s）為一未知增益函數，當且僅當小增益條件

M（jω）Δ（jω）＜1，ω∈R（7）

滿足時，系統對于所示系統對穩定的Δ（s）都是內部穩定的。外部干擾信號會在環路中逐漸衰減掉以實現內部穩定。

混合靈敏度問題是H∞魯棒控制器設計中常用的設計方法，其將系統的魯棒性問題及跟蹤性能問題轉化為一般靈敏度問題進行求解，其設計原理如圖6所示。

圖6中rec、e、u、d、y和z分別為參考輸入、跟蹤誤差、控制信號、干擾信號、輸出信號、觀測信號。W1、W3分別為需要設計的靈敏度、補靈敏度加權函數，W2為加性不確定性加權函數。

靈敏度函數S（s）表達式如下：

其反映了系統追蹤信號的能力及對擾動的一致能力，一般要求其在低頻段增益越小越好。

補靈敏度函數T（s）表達式如下：

其反映了系統對高頻不確定性擾動的抑制能力，一般要求其在高頻段增益越小越好。

其可避免控制電壓的飽和，同時又影響控制系統的帶寬，因此其增益應適當選擇既不能過大又不能過小。根據魯棒控制定理，在加權函數的設計過程中需滿足：

2.2 魯棒控制器設計與仿真

根據上文設計加權函數可得：

將上述加權函數代入混合靈敏度框圖，得到廣義被控模型P（s）并求解魯棒控制器模型：

式（15）為基于剛體模態辨識模型式（5）設計的H∞控制器模型，式（16）為基于剛性模態及柔性模態式（6）設計的H∞魯棒控制器模型。下面以式（15）分析H∞魯棒控制器性能。

由圖7可知所設計的魯棒控制器在低頻段呈現了積分效應，在中頻段呈現了類似PD控制器的頻響特性。

3 實驗

對所設計的H∞魯棒控制器進行靜態懸浮實驗，以剛體模態控制器為例，其效果如圖8所示。

由圖8可知，轉子超調量較小，在1.0s內便完成了轉子的靜態懸浮，具有較好的起浮特性。

圖9為磁懸浮軸承實驗臺添加1～150Hz一系列正弦激勵的響應瀑布圖。從圖中可以看出，在轉子系統剛體模態處，幅值出現了峰值，其振動幅值較小，體現了H∞魯棒控制器對轉子系統剛體模態的控制效果。

4 結語

本文基于正交多項式擬合原理對轉子系統剛體模態及彎曲模態進行了系統頻響辨識，建立了磁懸浮軸承系統被控模型，通過磁懸浮軸承掃頻實驗驗證了通過擬合模型的準確性。隨后基于混合靈敏度魯棒控制器設計方法，對辨識的系統被控模型進行H∞魯棒控制器設計。實驗結果表明，基于系統辨識的魯棒控制器應用于磁懸浮軸承系統中，具備較好的起浮特性及對剛體模態的控制效果，驗證了基于模型辨識的魯棒控制器設計的有效性及可行性。

參考文獻：

［1］ MUSHI S E， LIN Z L， PAUL E. Stability analysis for a flexible rotor on active magnetic bearings subject to aerodynamic loads ［C］// Proceeding of the 12th International Symposium on Magnetic Bearings. ［S.I.： s.n.］2010： 22-25.

［2］ RAN S L，HU Y F，WU H C. Design，modeling，and robust control of the flexible rotor to pass the first bending critical speed with active magnetic bearing［J］. Advances in Mechanical Engineering，2018，10（2）：168781401875753.

［3］ VAZQUEZ J A，MASLEN E H，AHN H J，et al. Model identification of a rotor with magnetic bearings［J］. Journal of Engineering for Gas Turbines and Power，2003，125（1）：149-155.

［4］ 孫喆，趙晶晶，時振剛. 電磁軸承支承柔性轉子模型測試與辨識［J］. 機械工程學報，2016，52（8）：16-22.

［5］ 傅志方，華宏星. 模態分析理論與應用［M］. 上海：上海交通大學出版社，2000.

［6］ 陳穎，陳懷海. 一種二自由度系統物理參數識別方法［C］// 第十屆全國振動理論及應用學術會議. 南京：中國振動工程學會，2011：207-213.

［7］ 王彤，張令彌. 有理分式正交多項式頻響函數模態參數識別［J］. 航空學報，2003，24（2）：140-143.

［8］ 周衡，金超武. 基于H∞和干擾觀測器的磁懸浮軸承干擾抑制方法［J］. 機械制造與自動化，2022，51（3）：149-151，158.