基于干擾觀測器的AUV三維路徑滑模跟蹤控制

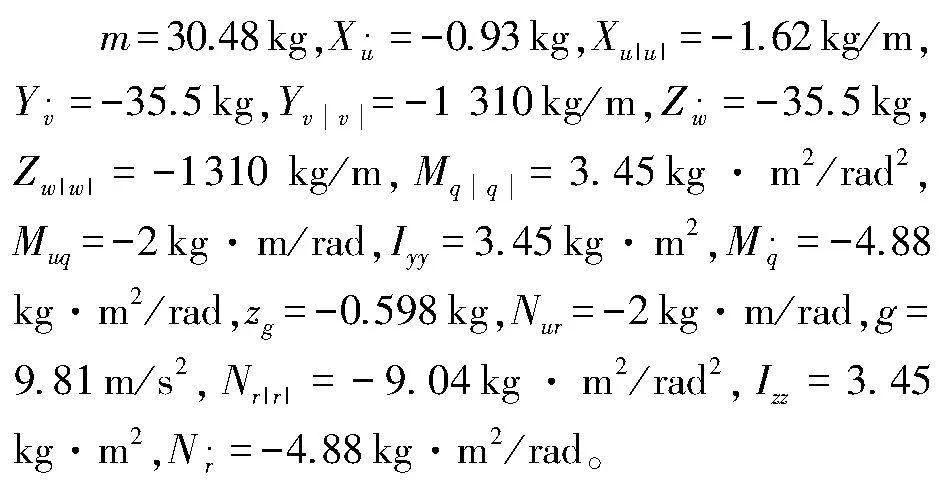
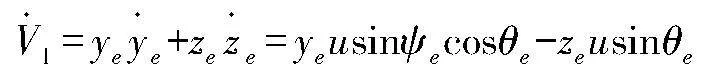
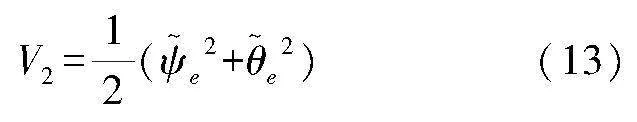
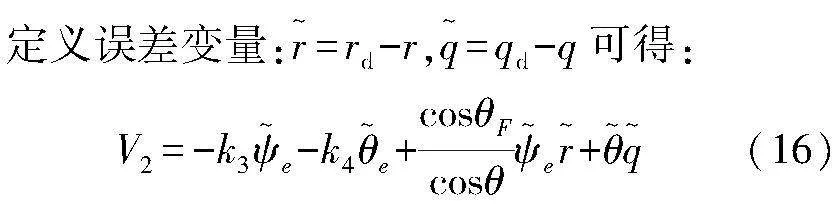
摘 要：為了確保欠驅(qū)動自主式水下機(jī)器人（AUV）在受到外界干擾情況下仍然可以實(shí)現(xiàn)對三維路徑的跟蹤控制，設(shè)計(jì)基于干擾觀測器的反步滑模控制器。針對欠驅(qū)動AUV 5自由度狀態(tài)方程，考慮外界干擾對AUV運(yùn)動的影響，設(shè)計(jì)干擾觀測器實(shí)時(shí)估計(jì)干擾；通過欠驅(qū)動AUV的狀態(tài)方程與三維路徑跟蹤誤差模型得到系統(tǒng)的鎮(zhèn)定模型；利用得到的干擾估計(jì)值，設(shè)計(jì)反步滑模復(fù)合控制器來控制AUV實(shí)現(xiàn)三維路徑跟蹤，并通過Lyapunov穩(wěn)定性理論證明閉環(huán)系統(tǒng)漸近穩(wěn)定。仿真結(jié)果表明：該控制器對欠驅(qū)動AUV實(shí)現(xiàn)三維路徑的精確跟蹤有良好的控制效果和抗干擾能力。

關(guān)鍵詞：欠驅(qū)動自主水下機(jī)器人；三維路徑跟蹤；干擾觀測器；反步滑模控制

中圖分類號：TP242.2文獻(xiàn)標(biāo)志碼：A文章編號：1671-5276（2024）03-0209-06

Sliding Model Tracking Control for AUV Three Dimensional Path Based on Disturbance Observer

Abstract：In order to ensure that the underactuated autonomous underwater vehicle （AUV） can still track and control the 3D path in the case of external interference， a backstepping sliding mode controller based on disturbance observer is designed. According to the 5-DOF state equation of underactuated AUV， an interference observer is designed to estimate the interference in real time considering the influence of external interference on the motion of AUV. The stabilization model of the system is obtained through the state equation of the underactuated AUV and the 3D path tracking error model. A backstepping sliding mode composite controller is designed to control the AUV and realize the 3D path tracking. The closed-loop system is proved to be asymptotically stable by Lyapunov stability theory. The simulation results show that the controller has good control effect and anti-interference ability for the accurate tracking of 3D path of underactuated AUV.

Keywords：underactuated autonomous underwater vehicle; 3D path tracking; nonlinear disturbance observer; backstepping sliding mode control

0 引言

自主水下機(jī)器人（AUV）由于具有較高的機(jī)動性和系統(tǒng)可靠性，在實(shí)現(xiàn)海洋科學(xué)調(diào)查、水下勘探和海洋目標(biāo)探查中起到重要作用［1］。AUV的路徑跟蹤控制是實(shí)現(xiàn)以上任務(wù)的保障。但由于AUV在復(fù)雜的海下環(huán)境作業(yè)時(shí)易受風(fēng)、浪等干擾的影響［2］，因此提高AUV在路徑跟蹤過程中的抗干擾能力有重要意義。

近年來，AUV的路徑跟蹤問題已引起學(xué)者們廣泛關(guān)注。文獻(xiàn)［3］針對AUV水平面模型，基于視線導(dǎo)引法建立跟蹤誤差模型，在控制器設(shè)計(jì)中結(jié)合模型預(yù)測算法，提高了AUV在水平面軌跡跟蹤的精度。文獻(xiàn)［4］針對AUV水平面模型受到干擾的情況，設(shè)計(jì)了基于干擾觀測器的滑模控制器，補(bǔ)償外界干擾帶來的影響，提高了AUV在水平面的跟蹤性能。文獻(xiàn)［5］對于欠驅(qū)動AUV受到干擾以及模型不確定性情況下的水平面路徑跟蹤問題，設(shè)計(jì)了基于自適應(yīng)反步控制算法與模糊控制算法結(jié)合的控制器，提高系統(tǒng)的抗干擾能力。針對AUV在垂直面的路徑跟蹤問題，文獻(xiàn)［6］將Lyapunov直接法與反步法結(jié)合設(shè)計(jì)控制器，使AUV以期望的合成速度跟蹤預(yù)定的深度路徑。文獻(xiàn)［7］設(shè)計(jì)了靜態(tài)輸出反饋控制器來提高AUV在垂直面的跟蹤精度。上述文獻(xiàn)只研究了AUV在水平面或垂直面的路徑跟蹤問題。文獻(xiàn)［8］通過運(yùn)用“虛擬向?qū)А狈ń⑷S路徑跟蹤誤差模型，采用濾波反步算法，解決了AUV三維路徑跟蹤控制問題。文獻(xiàn)［9］使用反步法設(shè)計(jì)了具有非線性動態(tài)特性的控制器，并應(yīng)用到欠驅(qū)動AUV的三維軌跡跟蹤控制上，提高了AUV三維路徑的跟蹤性能。文獻(xiàn)［10］針對欠驅(qū)動AUV 6自由度模型受到不確定性影響，在控制器設(shè)計(jì)中將對角回歸神經(jīng)網(wǎng)絡(luò)與S面控制算法結(jié)合，提高了跟蹤的精度。以上文獻(xiàn)均未考慮AUV受到外界干擾情況下的三維路徑跟蹤問題。

本文針對欠驅(qū)動AUV 5自由度模型受到干擾影響下的三維路徑跟蹤問題，設(shè)計(jì)了基于干擾觀測器的反步滑模控制器（DOBSMC），實(shí)現(xiàn)欠驅(qū)動AUV的三維路徑跟蹤控制。

1 欠驅(qū)動AUV數(shù)學(xué)模型

通過定義固定坐標(biāo)系{I}：E－ξηζ和剛體坐標(biāo)系{B}：O－xyz來描述欠驅(qū)動AUV的運(yùn)動，如圖1所示。圖中θ為縱搖角與ψ為艏搖角代表姿態(tài)向量。

忽略AUV的橫滾運(yùn)動，建立欠驅(qū)動AUV五自由度運(yùn)動學(xué)及動力學(xué)模型［11］：

式中：V=［uvwqr］T為定義在坐標(biāo)系{B}中的速度向量和角速度向量，其中u為縱蕩速度，v為橫蕩速度，w為垂蕩速度，q為縱搖角速度，r為艏搖角速度；η=［xyzθψ］T是AUV定義在坐標(biāo)系{I}中的位置向量和姿態(tài)向量，x、y、z為AUV位置向量；B代表質(zhì)量及慣性矩陣；C（V）代表科氏向心力矩陣；D（V）代表流體阻尼矩陣；g（η）=［000MHS0］T為重力和浮力產(chǎn)生的恢復(fù)力矩向量；J（η）為坐標(biāo)系{I}與坐標(biāo)系{B}之間的轉(zhuǎn)換矩陣；τ為AUV的驅(qū)動力和力矩；d為AUV所受到的外界干擾。將式（1）中的動力學(xué)模型展開可以得到：

2 干擾觀測器的設(shè)計(jì)

定義狀態(tài)變量x=x1x2x3x4x5T，其中：x1=u，x2=v，x3=w，x4=q，x5=r。

把狀態(tài)方程（2）改寫成向量形式：

構(gòu)造干擾觀測器如下：

定義觀測誤差：

3 DOBSMC設(shè)計(jì)

3.1 三維路徑跟蹤誤差模型

式中：Δξ=ξk+1－ξk；Δη=ηk+1－ηk；Δζ=ζk+1－ζk。

基于參考文獻(xiàn)［12］得到跟蹤誤差模型：定義P0=［ξ0η0ζ0θψ］是O在坐標(biāo)系{I}的位置和姿態(tài)，PP=［ξkηkζkθFψF］是P在坐標(biāo)系{I}的位置和姿態(tài)。在坐標(biāo)系{F}中的跟蹤誤差為：

Pe=［xeyezeθeψe］=R（P0－PP）

式中R是坐標(biāo)系{I}到坐標(biāo)系{F}的轉(zhuǎn)換矩陣，

對跟蹤誤差Pe求導(dǎo)有：

3.2 三維路徑跟蹤控制器設(shè)計(jì)

因AUV無垂向力與橫向力，故v與w很小，可忽略不計(jì)。又由于xe不需要進(jìn)行控制，所以結(jié)合式（2）和式（9）得到以下欠驅(qū)動AUV鎮(zhèn)定模型［13］：

式中：ud為期望縱蕩速度；ue為縱蕩速度誤差。

取Lyapunov函數(shù)

對V1求導(dǎo)有

設(shè)計(jì)艏搖角誤差期望值ψed和縱搖角誤差期望值θed為

式中：k1gt;0；k2gt;0。

令ψe=ψed，θe=θed，可得

取Lyapunov函數(shù)

對V2求導(dǎo)可得

式中：k3gt;0；k4gt;0。

取滑模函數(shù)：

式中：c1gt;0；c2gt;0；c3gt;0。

取Lyapunov函數(shù)

對V3求導(dǎo)有

設(shè)計(jì)控制器為：

式中k5、k6、k7、k8、s1、s2、s3均大于0。

根據(jù)干擾觀測器設(shè)計(jì)部分推導(dǎo)，干擾估計(jì)誤差可以收斂到0，所以可以得到：

因此

4 仿真實(shí)驗(yàn)

為驗(yàn)證本文所提出控制器的有效性，在Matlab2019a Simulink 中基于文獻(xiàn)［14］中AUV模型進(jìn)行數(shù)值仿真，具體參數(shù)如下：

干擾觀測器參數(shù)選取為：T1=1，T2=0，T3=0，T4=1，T5=1。

期望縱蕩速度ud為1m/s。

控制器參數(shù)選取為：

k1=0.2，k2=0.1，k3=1.0，k4=1.0，k5=10，c1=0.1，c2=0.1，c3=0.1，k6=1.0，k7=1.0，k8=10，ε1=0.1，ε2=0.1，ε3=0.1。

初始位姿向量：P0=（0000－0.5π）T。

所受外界干擾為：du=25，dv=dw=0，

dq=10sin（0.1t），dr=5sin（0.25t）+10。

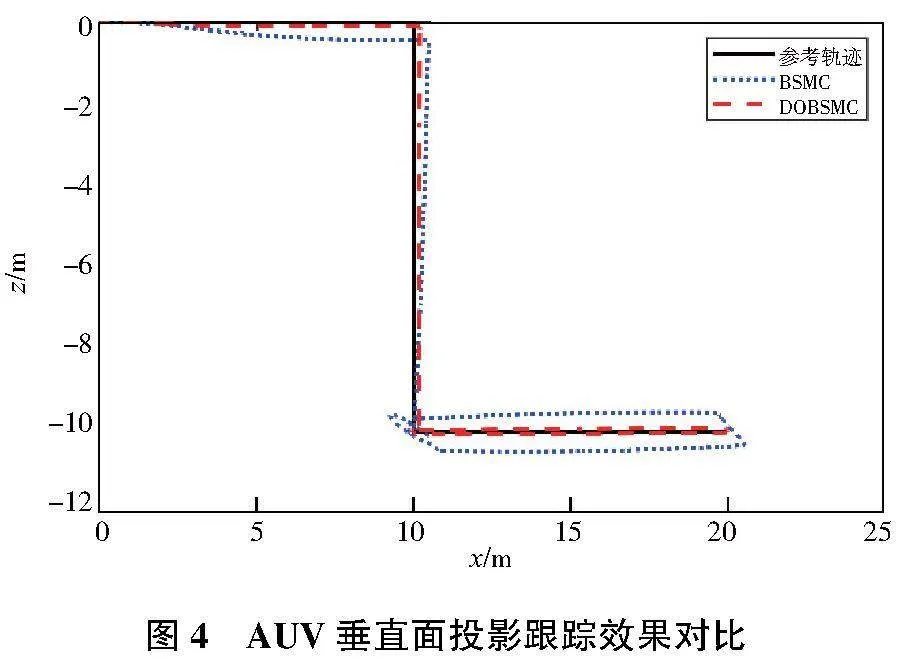
圖2是采用傳統(tǒng)反步滑模控制器（BSMC）與本文所設(shè)計(jì)的DOBSMC作用下的欠驅(qū)動AUV跟蹤路徑與期望路徑的對比圖。圖3和圖4是AUV三維路徑分別在水平面投影與垂直面投影的跟蹤效果對比。當(dāng)要求AUV實(shí)現(xiàn)三維路徑跟蹤任務(wù)時(shí)，跟蹤路徑與期望路徑越相近，說明跟蹤效果越好。從圖中明顯可以看出，BSMC的跟蹤路徑與期望路徑的偏差較大，而采用DOBSMC的跟蹤效果較好。

圖5是DOBSMC作用下的y方向與z方向上的跟蹤誤差。從圖中可以看出誤差分別在25s、15s左右時(shí)達(dá)到了峰值0.075m、0.055m，之后誤差均穩(wěn)定在0.05m范圍內(nèi)。

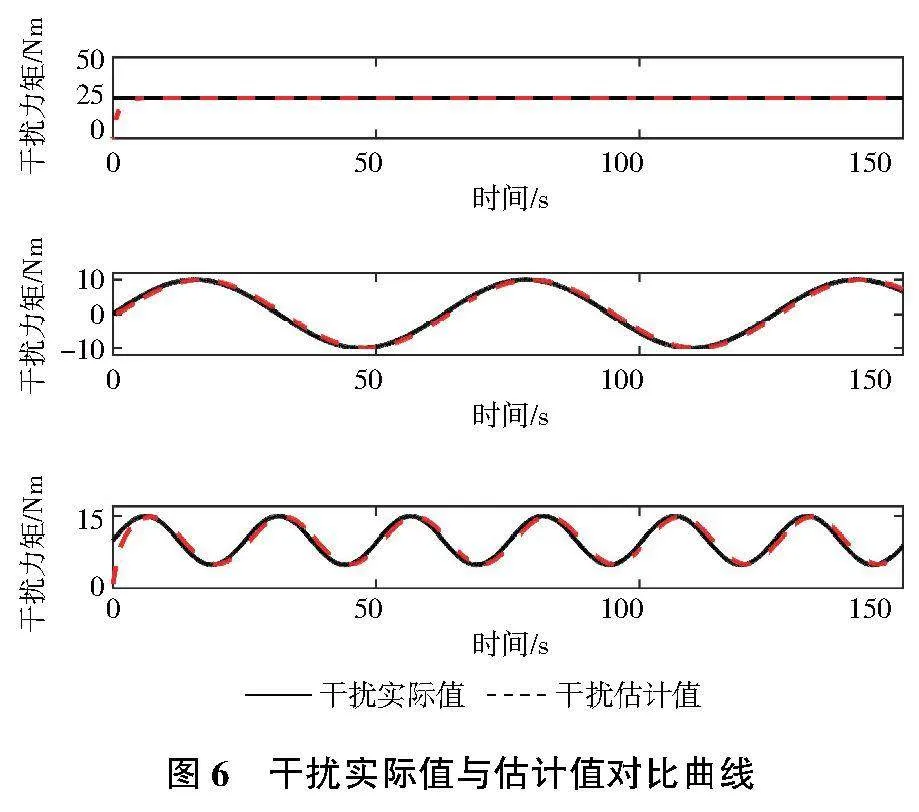
圖6為干擾實(shí)際值與干擾觀測器得到的估計(jì)值對比曲線。由圖可知，干擾觀測器可以實(shí)現(xiàn)對外界干擾的估計(jì)。

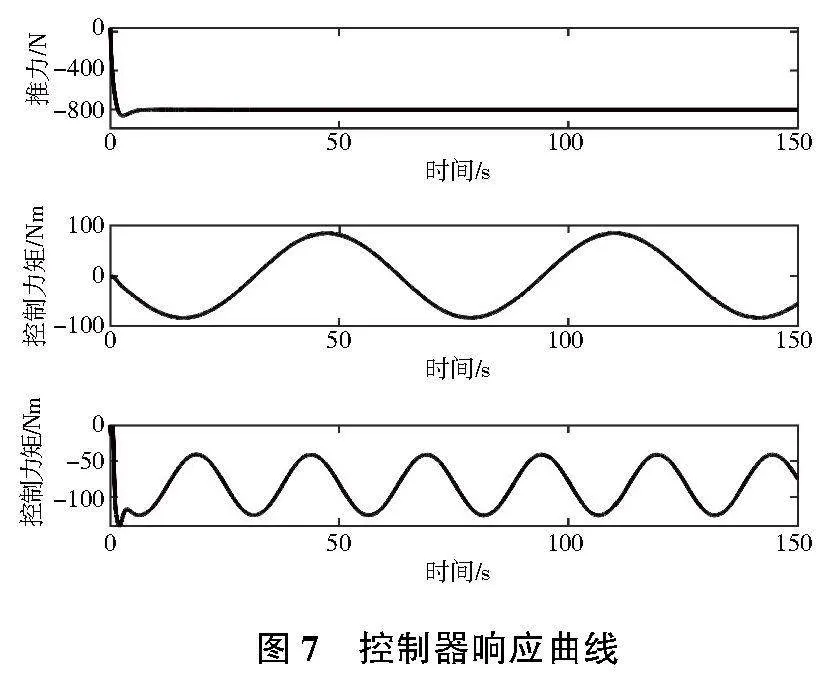
圖7是軸向推力X、縱搖控制力矩M以及艏搖控制力矩N的響應(yīng)曲線。

圖8是縱蕩速度u的響應(yīng)曲線，通過對式（2）的分析，縱蕩速度只與軸向推力X有關(guān)，軸向推力X直接決定了縱蕩速度u的大小。仿真結(jié)果顯示，當(dāng)軸向推力X穩(wěn)定在800N后，在其控制下縱蕩速度u最終收斂到期望值1m/s。

5 結(jié)語

通過對欠驅(qū)動AUV的5自由度模型與跟蹤誤差模型的簡化得到系統(tǒng)鎮(zhèn)定模型，考慮AUV受到干擾影響，設(shè)計(jì)了DOBSMC。仿真得到了AUV跟蹤的效果對比曲線以及位置跟蹤誤差曲線、干擾估計(jì)曲線、控制力矩和縱蕩速度的響應(yīng)曲線。結(jié)果表明該控制器能夠提高AUV三維路徑的跟蹤精度，且能有效抑制外界干擾對系統(tǒng)性能造成的影響。

參考文獻(xiàn)：

［1］ 王鵬. 欠驅(qū)動自主水下航行器的航跡跟蹤控制研究［D］. 秦皇島：燕山大學(xué)，2021.

［2］ 王芳，萬磊，李曄，等. 欠驅(qū)動AUV的運(yùn)動控制技術(shù)綜述［J］. 中國造船，2010，51（2）：227-241.

［3］ 郭亦平，王益民，任元洲. 基于視線導(dǎo)引法的AUV軌跡跟蹤控制技術(shù)研究［J］. 聲學(xué)與電子工程，2018（4）：32-36，40.

［4］ 李廣有，王娜，尹慶華. 欠驅(qū)動AUV基于干擾觀測器的滑模控制［J］. 機(jī)械制造與自動化，2022，51（2）：177-180.

［5］ 王金強(qiáng)，王聰，魏英杰，等. 未知海流干擾下自主水下航行器位置跟蹤控制策略研究［J］. 兵工學(xué)報(bào)，2019，40（3）：588-591.

［6］ YU C Y，XIANG X B. Vertical plane path following control of an under-actuated autonomous underwater vehicle［C］//2016 IEEE International Conference on Underwater System Technology：Theory and Applications （USYS）. Penang，Malaysia：IEEE，2017：37-41.

［7］ SUBUDHI B， MUKHERJEE K， GHOSH S. A static output feedback control design for path following of autonomous underwater vehicle in vertical plane［J］. Ocean Engineering，2013，63：72-76.

［8］ 王宏健，陳子印，賈鶴鳴，等. 基于濾波反步法的欠驅(qū)動AUV三維路徑跟蹤控制［J］. 自動化學(xué)報(bào)，2015，41（3）：631-645.

［9］ LI Y， WEI C， WU Q， et al. Study of 3 dimension trajectory tracking of underactuated autonomous underwater vehicle［J］. Ocean Engineering，2015，105：270-274.

［10］ 周則興. 基于DRNN-S控制的AUV三維軌跡跟蹤方法［J］. 艦船科學(xué)技術(shù)，2021，43（21）：96-99，178.

［11］ 金鴻章，姚緒梁. 船舶控制原理［M］. 2版. 哈爾濱：哈爾濱工程大學(xué)出版社，2013.

［12］ 姚緒梁，王曉偉，蔣曉剛，等. 海流干擾下的欠驅(qū)動AUV三維路徑跟蹤控制［J］. 哈爾濱工業(yè)大學(xué)學(xué)報(bào)，2019，51（3）：37-45.

［13］ 王曉偉，姚緒梁，夏志平，等. 欠驅(qū)動AUV三維直線路徑跟蹤控制［J］. 控制工程，2020，27（6）：977-983.

［14］ PRESTERO T . Verification of a six-degree of freedom simulation model for the REMUS autonomous underwater vehicle［D］. ［S.I.］：Massachusetts Institute of Technology， 2001.