關注數(shù)學理解 提升數(shù)學素養(yǎng)

[摘 要] 新課標背景下，初中數(shù)學教學越來越關注對學生綜合能力和綜合素養(yǎng)的培養(yǎng). 為了達到這一要求，教師應從學生實際學情出發(fā)，創(chuàng)設貼近學生實際的探究活動，以此激發(fā)學生的探究欲，讓學生更好地體驗與理解、思考與探索知識，進而實現(xiàn)對知識的融會貫通，切實提高發(fā)現(xiàn)、分析和解決問題的能力，發(fā)展學生數(shù)學核心素養(yǎng).

[關鍵詞] 數(shù)學理解;數(shù)學核心素養(yǎng);初中數(shù)學

問題的提出

無理數(shù)是數(shù)的又一次擴充，引進無理數(shù)對數(shù)學的發(fā)展有著重要意義. 相對于有理數(shù)，無理數(shù)更加抽象，其中隱含的“無限”“不循環(huán)”給學生的理解帶來了困難. 為了讓學生理解和接受無理數(shù)，應該讓學生感受無理數(shù)邏輯上的合理性.

在無理數(shù)概念教學中，首先從開方開始，即“如果a2=2，則a是多少”. 教材中采用“二分法”逐步推導，確定a的個位、十分位、百分位……，從而得到a是一個無限不循環(huán)小數(shù)[1]. 這樣做的優(yōu)點是可以將前后知識聯(lián)系起來，但是其不足是學生容易產生錯覺，認為無理數(shù)就是開方開不盡的數(shù)，可見通過經歷以上過程，學生雖然知道無理數(shù)的概念，但是并不能讓學生真正地理解和接受無理數(shù)的概念.

教材中給出以上推理過程，其目的是讓學生更好地接受無理數(shù). 不過從教學反饋來看，大多數(shù)學生雖然能夠看得懂，但是卻不能獨立完成證明. 很多學生的證明過程推理模糊，缺乏條理性，而邏輯論證對無理數(shù)概念的建立有著不容忽視的作用，為了讓學生更好地理解和接受無理數(shù)邏輯上的合理性，筆者嘗試采用一種圖形證法，以此借助圖形的直觀幫助學生理解這個命題及其證明，發(fā)展學生邏輯推理素養(yǎng).

教學過程

1. 操作與思考

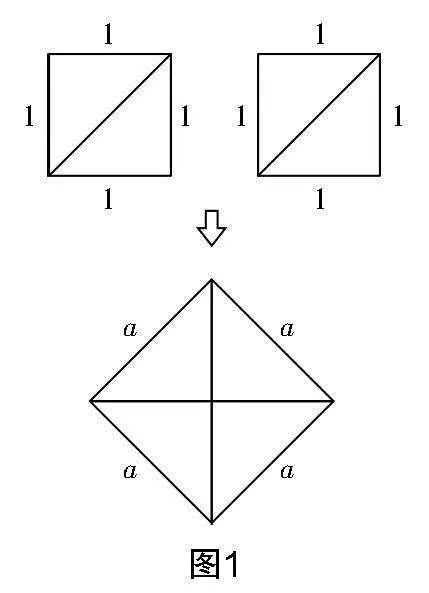
問題1：如圖1，現(xiàn)有兩個邊長為1的小正方形，將其沿對角線剪開，得到一個大正方形，大正方形的邊長是多少？

2. 操作與推理

教師給出假設后，通過創(chuàng)設問題引導學生主動參與推理，過程如下.

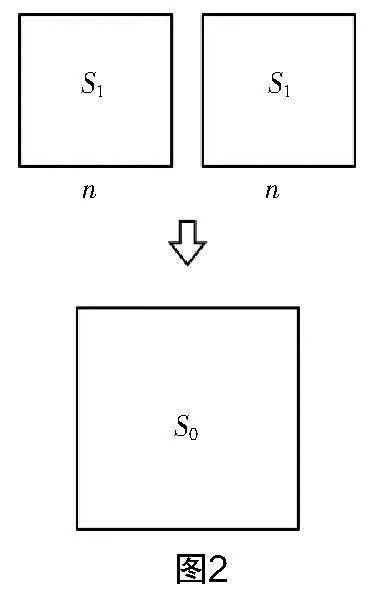
問題2：如圖2，現(xiàn)有兩張邊長為n的小正方形紙片，面積記為S，若將兩個小正方形紙片拼成一個正方形，則可以得到一個邊長為m的大正方形，大正方形的面積記為S. 由此你能得到怎樣的數(shù)量關系？

學生活動：結合已知易得S=2S，即2n2=m2.

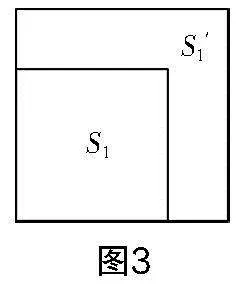
問題3：如圖3，將其中一個小正方形移到大正方形中，兩個正方形未重疊部分的面積記作S′1，由此你能得到怎么的數(shù)量關系？

學生活動：學生通過觀察、推理，易知S=S′.

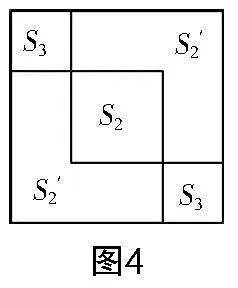
問題4：如圖4，在原有的基礎上，將另一個小正方形也放到大正方形中，你有哪些發(fā)現(xiàn)？

學生活動：根據(jù)圖形對稱性可知，兩個小正方形重疊部分為正方形，其邊長為2n-m，面積記為S;未重疊部分的兩個小正方形邊長為m-n，面積記為S;余下兩個L型圖形全等，其面積記為S′，則S+S′=S+S′+S，即S=2S.

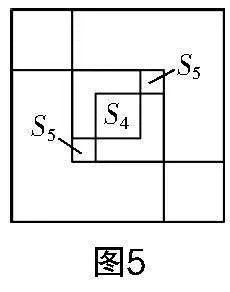
問題5：如圖5，若將得到的兩個面積為S的小正方形平移到S中，你又有什么發(fā)現(xiàn)？

學生活動：學生結合圖5及以上探究經驗，得到S=2S .

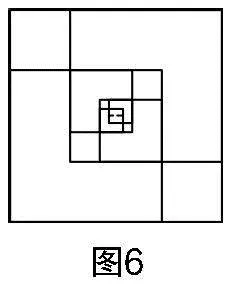
問題6：如圖6，如果按照以上步驟繼續(xù)操作下去，你還能得到怎樣的數(shù)量關系？

學生活動：學生結合以上規(guī)律，又得到S=2S，S=2S……

問題7：已知m、n是正整數(shù)，由此你能得到什么？

師生活動：學生先獨立思考，教師給予適時指導，學生通過合作探究得到正方形S、S、S……的邊長都是正整數(shù).

問題8：如圖6，正方形在不斷變小，這樣正方形的邊長也會bW60XynsR9spzj1+pozt5LxndM2pXmO7Ti63My9LIxE=不斷減小，那么正方形的邊長是整數(shù)，成立嗎？

設計意圖 教學中，教師巧妙地結合圖形讓學生操作、觀察、聯(lián)想、驗證，由此發(fā)現(xiàn)若假設成立，則小正方形的邊長均為正整數(shù)，但是根據(jù)“最小數(shù)原理”，若按照以上過程無限迭代下去，必然會存在正方形的邊長小于1的情況，由此借助圖形完成證明. 在此過程中，教師預留時間讓學生觀察、推理，有利于激發(fā)學生的主體性，培養(yǎng)學生邏輯推理能力.

3. 操作與推廣

設計意圖 通過適度的拓展延伸，幫助學生跳出圖形只能是正方形的局限，拓寬學生的視野. 同時，在此過程中，教師將探究的主動權交給學生，這樣一方面可以檢測學生對該圖形證法的掌握情況，另一方面可以借助幾何直觀，培養(yǎng)學生邏輯推理能力.

設計意圖 經歷以上證明過程不僅可以進一步強化已有知識方法的理解，而且通過有效對比，可以讓學生更加直觀地感知“有限”與“無限”，有利于知識的內化.

這樣借助圖形的直觀，凸顯概念的本質，有利于概念的深化，有利于鍛煉學生邏輯推理能力，促進學生數(shù)學核心素養(yǎng)的落實.

教學思考

1. 開展自主探究，鼓勵邏輯論證

數(shù)學學習是一種傳承，更是一種發(fā)展. 教學中教師不是直接將知識教給學生，而是提供機會讓學生去發(fā)現(xiàn)、去探索、去創(chuàng)造，讓學生用數(shù)學的眼光觀察世界，培養(yǎng)學生的思維能力，提升學生的數(shù)學素養(yǎng).

2. 巧借直觀想象，提升推理能力

直觀想象和邏輯推理是數(shù)學核心素養(yǎng)的重要組成部分，它們既相對獨立，又相互融合. 直觀想象為邏輯推理提供方向，而邏輯推理為直觀想象提供依據(jù)，兩者協(xié)調發(fā)展有利于學生更好地理解數(shù)學，樹立善于思考、嚴謹求學的科學精神，提高自主學習、實踐探究的能力.

在本課教學中，教師引導學生從正方形入手，讓學生經歷操作、猜想、交流、推理等過程，使得推理過程變得更加生動、有趣. 在這一過程中，學生深度思考與探索，提升了數(shù)學思維品質.

總之，數(shù)學教學不是簡單地讓學生接受知識，更重要的是讓學生理解知識. 因此，教師要改變單一的講授式教學，要創(chuàng)造機會讓學生去發(fā)現(xiàn)、去探索、去歸納，從而讓學生獲得對知識真正的理解，有效激發(fā)學習熱情，提高學習品質.

參考文獻：

[1]劉洪超，周楊. 歷史視角的“無理數(shù)”概念教學思考——基于對無理數(shù)概念教學淺表化現(xiàn)象的分析[J]. 中學數(shù)學雜志，2021（02）：27-30.