創新而行，讓數學教育智慧而有溫度

【摘 要】數智時代，推進技術與數學課程的深度融合，離不開數學可視化教學和探究實驗式學習。讓數學教育更智慧，需要讓思維“看”得見，為數學理解構建場景；讓數學教育有溫度，需要關注學生，站在學生立場設計場景。唯有教研創新，才有學科育人，才能在“人—知”互動中重塑數學教育新形態。從融合教學到賦能教研，以“質”致遠，創“新”而行，正是推進數學教育數智化轉型的必由之路。

【關鍵詞】創新；教育家精神；高中數學；教育數字化

【中圖分類號】G451 【文獻標志碼】A 【文章編號】1005-6009（2024）31-0094-03

【作者簡介】張志勇，江蘇省常州市第五中學（江蘇常州，213023）教師，正高級教師，“蘇教名家”培養工程培養對象，江蘇省“333高層次人才培養工程”培養對象，江蘇省高中數學名師工作室主持人。

數智時代，讓數學教育更智慧，就需要推進技術與數學課程的深度融合，讓技術真正融入教師的教與學生的學，豐富課程資源，為理解概念創設背景，為探索規律啟發思路，為解決問題提供路徑。有溫度的數學教育，要求關注學生，為學生的自主學習創造條件；構建探究場景，啟發學生像數學家一樣思考。當然，更重要的恰是教師的教研創新，唯有站在學生立場探討更多可能，才能在“人—知”互動中重塑數學教育新形態。

一、數學可視化教學，讓思維“看”得見

數學的高度抽象性，既是數學學科的價值特點所在，也是數學教育的難點痛點所在。因為數學知識難以被直接感知，更難以被理解和內化；往往教數學的人不知如何去言傳，學數學的人不知如何去意會。因此，技術賦能的著力點便在于數學的具象化，即挖掘技術于數學的表征優勢，在抽象的數學與形象的現實間構建聯系通道，使數學變得可見并且可操作，從而突破“意會”與“言傳”間的障礙。

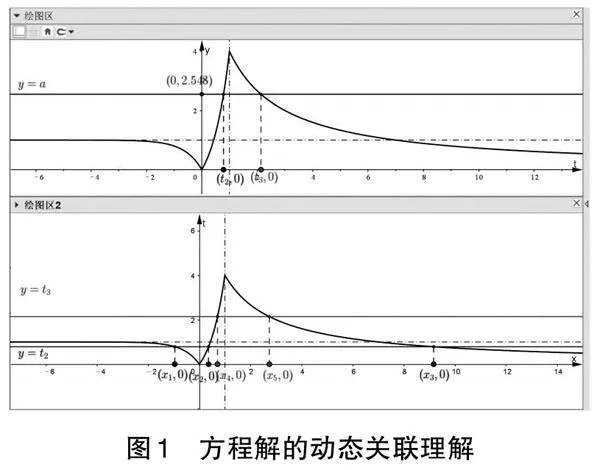
以問題“已知函數f（x）=[|5x-1|， x<18x+1，x≥1]，若方程f（f（x））=a恰有5個不同的實數根，求實數a的取值范圍”為例，通常的教學策略是數形結合加換元化歸：畫出函數圖象，將方程解的問題轉化為圖象交點的判斷；設置臺階，借助換元法將復雜方程f（f（x））=a分解轉化為方程組[f（t）=at=f（x）]。本題的難點在于參數變化引發的多情形討論，而兩個方程的相互關聯、彼此牽制讓分類討論愈加復雜。把學生從“傻傻分不清楚”的混沌模糊狀態拖拽出來的最好方式，就是創設圖1所示的動態可視化情境：在參數a的變化過程中，考察方程f（t）=a，t=f（x）間的關聯對應。有了整體模型的認知基礎，再進行精細的運算刻畫便水到渠成。

就上例而言，兩個方程的關聯對應和取值范圍的反向限制是學生認知的難點，借助數字技術的多元表征、直觀形象優勢，恰可以構建“所見即所得”的數學情境，為學生的數學理解創設條件。信息技術賦能教學，可以為教師的“言傳”加持“圖示”表達，可以為學生的數學學習插上想象的翅膀，從而讓學生在動態關聯情境中深度思考。

二、數學實驗式學習，讓探究“做”得到

信息技術與數學教育的深度融合，不只是賦能教師的教，實現數學對象的不同表征方式的多元呈現，為數學教學提供豐富的資源和環境，讓數學教育更智慧；更可以推動學生數學學習方式的變革，讓學生通過數學實驗活動，從直觀、想象到猜想、發現，親歷數學知識的建構過程，在“做”數學的過程中豐富感知，在直觀感知的基礎上建立表象，在表象的提取與運用中發展想象能力。

以“正方體截面的探究”教學為例，用一個平面截正方體，截面的形狀將會是什么樣的？面對這樣的問題，學生往往很難考慮周全，與其直接告知結果，不如讓他們自主實驗探明究竟。

如圖2，拖動點L、M、N的位置，改變截面位置，可以清楚地“看見”截面形狀，呈現出從三角形、四邊形到五邊形、六邊形的不同樣態。學生從平面視圖中可以觀察到截面邊的平行特征，聯想“正方體中對面平行”的原因，從而在構建“面面平行的性質定理”應用模型的同時，找尋到截面圖形的分類原則（將正方體的６個側面分為前后、左右和上下３對平行側面，整體考慮截面與這三對側面是否相交）。進一步地，探究“為什么不能截出邊數超過６的截面？”“為什么不能截出直角三角形和直角梯形？”等思辨性問題，從而推證出“有直角內角的截面必為矩形”“三角形截面必為銳角三角形”等結論。

讓數學教育有溫度，就需要把時間還給學生，鼓勵學生自主探究。通過實驗方式來學習數學，可以把抽象的結論寓于其中，使學生經歷從具體到抽象的過程，從而讓學生見到數學的全貌、體會數學的全過程。因為核心素養的發展與知識技能的傳授不同，不能單純依賴教師的教，而是需要學生真正參與其中；不能單純依賴記憶與模仿，而是需要感悟與思維。

三、數學發散性研討，讓創新“在”身邊

什么是“融合”？“融”是融化溶解，強調的是過程方法；“合”是交匯合成，展現的是目標結果。深度融合，意味著技術與數學、教學已經融為一體、難分彼此。推動技術與數學課程的深度融合，就需要破除工具思維。在這里，技術不再只是“漸進式修修補補”的工具，其應用也不限于改進教學優化教學、推動理解提升質量。技術更應該成為教育變革的催化劑和新引擎，推動教育教學的系統改造和迭代更新，進而“創構”出教學內容呈現方式、學習資源獲取方式、教學人際互動樣態、教學空間秩序格局等煥然一新的教學時空。問渠那得清如許，為有源頭活水來。深度融合的進階之路，顯然依賴于教師的教研創新，通過教研探討更多的教學可能，基于實踐破除內卷，提升教學想象力。

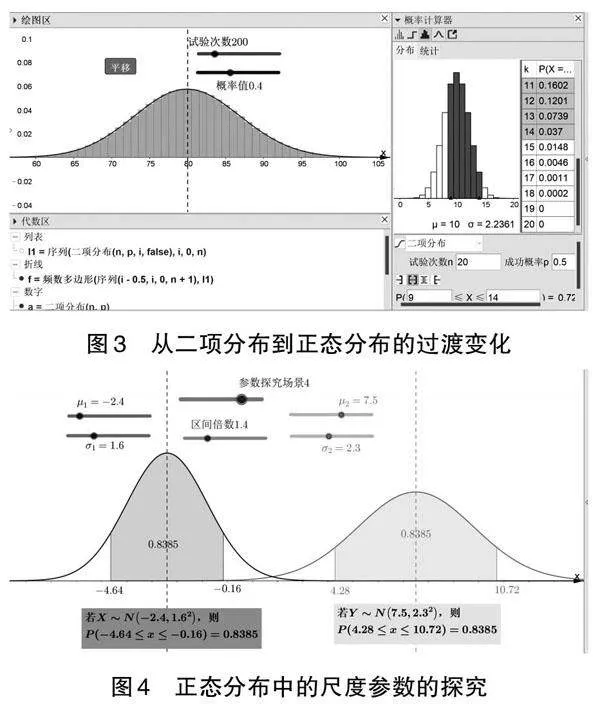
例如，正態分布作為重要的概率模型，有著廣泛的實用性和優美的數學特性。面對學生“知道是什么，但不知道為什么”的學習困惑，教師可以應用GeoGebra構建的正態分布可視化學習環境，為正態分布的探討學習提供無限“可”與“能”。圖3中，教學從二項分布逼近導入，幫助學生建構“二項分布逼近正態分布”的數學理解。雖然沒有微積分的推演論證，但在可視化技術的支持下，可以幫助學生發展數學眼光、形成數據意識。圖4中構建的“所見即所得”的關聯情境，以“形”之長彌“數”之短，幫助學生建構對尺度參數的認識。從正態曲線的“相似性”到不同正態分布間的相互轉化，源于教材卻又高于“3σ原則”。這樣的可視化學習并沒有弱化學生的邏輯抽象能力，而是帶來了更高的觀念滲透和更深的思維啟迪，讓學生有更多的機會和可能進行更高層次的數學思考和問題解決。

教研創新，首先體現在教學的科學性上，要求教師有“畫龍點睛”之能，能夠從數學知識中挖掘數學思想，從過程方法中提煉核心素養。因為數學教師的主要任務不是去創造數學概念，而是創造概念的數學理解方式，把數學的“學術形態”轉變為“教育形態”。更有意義的是，教師應把“點睛之筆”留給學生，激發學生的內在需求，形成某種心理張力，然后主動去想象、去探究。這是教學藝術，是更高維度上的教研創新。

從數學可視化教學到探究實驗式學習，從更智慧到有溫度，從融合教學到賦能教研，正是推進數學教育數智化轉型的必由之路。創新而行，讓數字之光點亮前行之途，以教育之力厚植幸福之本，是教師勤學篤行的動力源泉，更是求是創新的方向追求。

*本文系國家社會科學基金教育學一般課題“‘雙減’背景下義務教育階段作業設計研究”（BHA220139）、江蘇省教育科學“十四五”規劃課題“基于核心素養的高中數學大單元教學價值意蘊與路徑探析研究”（SJMJ/2021/10）階段性研究成果。