學生數學語言互譯能力提升策略研究

摘 要 數學閱讀是經過學生的認知加工、思維消化，通過學生自身的再創造活動轉換為文字、圖形、符號三種數學語言，從而納入其認知結構中。從數學文字、數學圖表、數學符號三個語言維度分析，發現學生的關鍵信息提取低效，圖表閱讀能力缺失，符號意義探究“泡沫化”，因此，須強化閱讀指導，擴大閱讀視角，滲透符號意識，助力學生在閱讀中提升數學語言互譯能力。

關 鍵 詞 小學數學；閱讀；數學語言；互譯能力

引用格式 李紅俠.學生數學語言互譯能力提升策略研究[J].教學與管理，2024（26）：49-51.

數學語言互譯是小學數學的難點。現有數學教材中存在大量與數學語言互譯相關的內容，從概念認知到公式運算再到應用題都涉及數學文字、數學圖表、數學符號三種數學語言在不同題型中的相互轉換，而學生的數學語言互譯能力不高，提取信息能力低下。因此，教師有必要分析學生數學語言互譯能力不強的原因，并探索相應的教學策略。

一、學生數學語言互譯存在的問題

通過對教材變遷的分析以及課堂教學的觀察，本文對數學文字、數學圖表、數學符號存在的問題進行剖析，以促使學生在不同題型中合理轉換數學語言。

1.數學文字：關鍵信息的低效化提取

針對常規性數學問題呈現出的情境簡單、結構清晰、結果有限的特點，學生無需思考，套用公式直接計算即可。可是面對非常規性數學問題時，學生需要分析數學文字中的語句，篩選和提取關鍵信息。通過對數學課堂的非參與性觀察，筆者發現小學生數學文字閱讀存在以下問題：（1）抓不住關鍵信息。如數量、單位、時間、人群等的具體屬性和轉換。例如，XX身高為1.4（厘米），這是由于學生沒有真正形成對數學單位具體的定量概念。也就是說，學生對1厘米、1米沒有形成具體的概念，這就需要我們在教學中將文字轉換成具化的圖表語言。（2）找不到題目中的隱藏條件。例如，由6個等邊三角形拼成的六邊形，等邊三角形的邊長是1，這個六邊形的周長是多少？看似條件未知，卻可以根據“等邊三角形每條邊都相等”這一隱藏條件，推出六邊形的周長。面對數學文字，學生篩選和提取關鍵信息的能力不足，這需要教師加強學生對數學閱讀方法的掌握，合理轉換三種數學語言。

2.數學圖表：“大視角”閱讀能力的缺失

數學圖表語言具有簡明直觀、概括性強、知識覆蓋面廣等特點。在解答圖表語言類題目的時候，學生要經歷理解圖表、分析圖表的過程，即數學語言的轉換過程。如何把圖表信息準確地轉換成文字？要求全面準確地識讀圖表內容，注重整體閱讀，“大視角”搜索有效信息。通過觀察學生課堂表現，發現學生閱讀圖表類語言存在以下問題：（1）閱讀視角狹窄化。有不少學生忽視表頭和表腳文字、混淆橫縱坐標標簽，這些是由于學生閱讀視角狹窄造成的。例如，柱形圖可以直觀顯示數據變化，但學生容易忽視數據細節；折線圖可以顯示數據變化趨勢，但學生容易忽視具體數值；餅狀圖可以直觀顯示各部分占比，但學生容易忽視各部分之間的比較。（2）“數”與“形”思想存在割裂。例如，學生不會利用圖表、線段等直觀手段幫助自己理解單位“1”并進行再分；在應用題學習中，面對題目中的已知條件，不會繪制示意圖幫助自己解決問題。

3.數學符號：“泡沫化”符號意義探究

符號語言是敘述語言的符號化，具有明顯的簡潔性、高度的概括性，但也抽象難懂[1][2]。通過調查發現，閱讀數學符號語言存在以下問題：（1）數學符號運用能力較弱。部分學生在解決數學問題時，無法有效運用符號進行表達和計算，這主要是因為他們在理解數學符號的邏輯關系和計算規則時存在困難。學生對數學符號的理解不夠清晰，往往只能機械地記住其代表的數值或關系，這導致他們在使用數學符號時缺乏靈活性。（2）數學符號感不強。無論在哪個學段，教師都應鼓勵學生用自己獨特的方式表示具體情境中的數量關系和變化規律，這是發展學生符號感的決定性因素。學生的數學符號感不強，是因為沒有為學生提供經歷“具體事物—學生個性化的符號表示—學會數學地表示”這一逐步符號化、形式化的過程。

二、優化學生數學語言互譯能力的策略

1.數學文字：加強閱讀指導，深化概念理解

（1）數學批注。在數學閱讀過程中，對閱讀材料進行批注，不僅能深化學生對數學概念、定理、公式等的理解，而且便于記錄學生學習數學的整個思維過程。第一步，將關鍵詞、易混詞圈出來。如“倍的認識”，教師要提示學生注意“A比B多幾倍”與“A是B的幾倍”的區別；第二步，厘清數量、單位、時間的具體屬性和轉換；第三步，通過批注提取數學文字中的信息。如，A比B多幾倍，A=（多的倍數+1）×B，A是B的幾倍，A=幾倍×B。數學批注可以以數學圖形、符號等形式出現，批注的過程是對閱讀內容歸納、挖掘、再思考、再整理、再反思的過程，是對數學概念、定理、公式等的理解過程，是提高學生運用數學知識解決實際問題，掌握數學方法、形成數學思想的重要途徑。

（2）說題練習。教師可以引導學生通過說題的方式將數學題目中的圖形、數學符號表征出來，建立文字與圖形之間的聯系[3]。第一步，明確題意，明白已知條件和問題；第二步，分析思考，明確問題中的已知條件及所涉及的數學概念等，進行知識點鏈接；第三步，篩選出解決問題所需要的數學信息，并通過文字語言將自己對問題的理解以及解決問題的基本思路說出來。如下題：

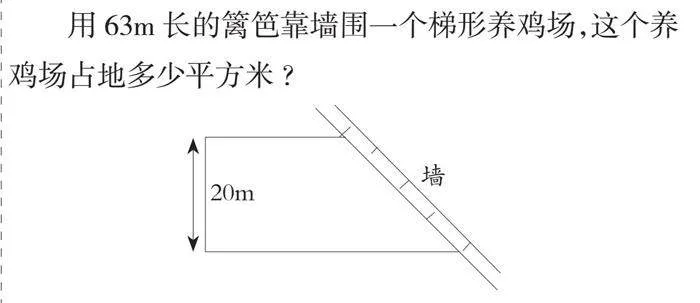
用63m長的籬笆靠墻圍一個梯形養雞場，這個養雞場占地多少平方米？

第一步：明確已知條件：用63米長的籬笆靠墻圍成一個梯形養雞場，圖形告訴我們所圍成的梯形是直角梯形，高為20米，所求問題：這個養雞場占地多少平方米？第二步：知識點鏈接，梯形面積=（上底+下底）×高÷2；第三步：觀察圖形，根據已知條件找出隱含條件，梯形上底與下底的和是43米，不需要分別求出上底和下底分別是幾米。這就需要學生及時鞏固梯形面積計算公式的理解和運用。通過說題的方式組織和鞏固自己在閱讀過程中所產生的想法，并完成數學語言間的轉譯。

2.數學圖表：擴大閱讀視角，整合“數”與“形”

圖形是數學研究的對象，也是數學思維和表達的工具。圖形可起到啟發思維、支持思維、喚起記憶的作用，有利于盡快找到解題思路。在解答應用題時，圖形可以把數量關系具體而形象地表達出來，簡明直觀而又極具概括性。

（1）“大視角”閱讀。一是觀察圖表，了解圖表的基本類型和元素：柱形圖——直觀顯示數據變化，折線圖——顯示數據變化趨勢，餅狀圖——直觀顯示各部分占比；圖表的基本元素：軸、刻度、數據點、數值、單位、顏色、標題、軸標簽、圖例等。二是閱讀圖表，學會從圖表中提取信息，明確圖表的目的和意義，可以用簡潔明了的語言描述圖表，這是學生形成個人見解的思維過程。三是制作圖表，通過制作圖表加深學生對圖表的理解，如價格標簽、天氣預報等。四是分析圖表，解讀圖表中數據的意義、分析數據的變化趨勢，結合圖表和數據，分析圖表所表達的主題和意義。

（2）整合“數”與“形”，助力學生形象思維。小學生在具象中學習起來會更加認真、更加投入。因此，在圖表圖形教學中，教師應整合“數”與“形”，以最大程度地幫助學生理解和掌握抽象的數學。例如，對“四邊形內角和為360°”的理解，可以通過現實化的圖形去驗證。①畫一畫，量一量，通過量角器去度量內角和度數；②剪一剪，折一折，將任意一個四邊形的四個角向內折，正好是一個周角；③撕一撕，拼一拼，四邊形的四個內角撕下來正好能拼成一個周角；④分一分，算一算，三角形的內角和是180°，把四邊形分成兩個三角形，每個三角形的內角和是180°，那四邊形的內角就是180°×2=360°。通過圖形語言將“四邊形內角和為360°”情境化[4]，通過規律探究，得出多邊形與分成三角形個數之間的關系，從特殊到一般，逐漸用符號表示多邊形內角和的一般模型：（n-2）×180°。

3.數學符號：滲透符號意識，兼顧符號的練與用

教師應引導學生充分經歷“具體情境—數學符號表示—符號語言釋疑”的認知過程，讓學生學會用符號語言表述數學知識，幫助學生形成符號意識。

（1）“運算”中培養，訓練符號思維。教師要引導學生在教學中挖掘符號意識，學會用符號語言表示數學知識。例如“找規律”一課，要求學生用簡化的符號把圖片的規律記錄下來，進行符號思維練習。有的學生用文字“大小大小大小”表示，有的學生用符號“△○△○△○”表示，有的學生用數字“1 2 1 2 1 2”表示。這既符合學生的特點，又有利于他們加深對符號的理解。

（2）“推理”中培養，把握符號工具。將解決具體問題的思維轉化為符號語言的表示，既有利于增強學生的數學符號意識，又有利于提高學生運用數學符號解決實際問題的能力，還能培養學生的數學語言表達能力。教師可以引導學生感受生活中的數字，班級、門牌號……知道這些都是利用符號化語言為社會生活提供方便。學生要用符號語言表示變化規律，體會符號語言的簡潔性、概括性，激活頭腦中潛在的符號意識。

（3）“轉化”中培養，加深符號理解。數學課程標準要求學生能夠利用數學符號去表示數、數量關系以及變化規律，這不僅要求學生理解數學符號，而且會利用數學符號表達關系并相互轉換。比如能夠對數學符號進行語言表述、圖形轉換以及關系式（數學符號）表達，這不僅是理解事物的關鍵，也是解決問題的需要。

（4）“探究”中培養，利用符號解決問題。教師要將數學符號有機融入學生的數學學習和生活中，讓學生真正體會到數學符號的實用性與優越性，使得符號語言逐漸成為學生表達數學的內在需求。如下題：

一件裙子、一條褲子、一件藍色上衣、一件白色上衣，有幾種搭配的方法？

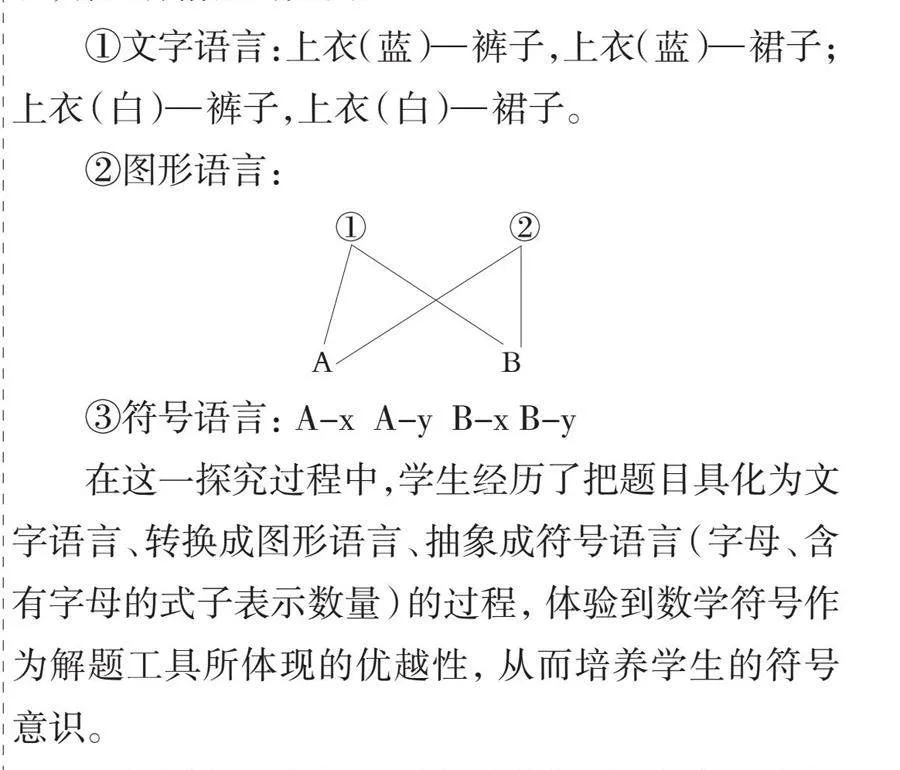
①文字語言：上衣（藍）—褲子，上衣（藍）—裙子；上衣（白）—褲子，上衣（白）—裙子。

②圖形語言：

③符號語言：A-x A-y B-x B-y

在這一探究過程中，學生經歷了把題目具化為文字語言、轉換成圖形語言、抽象成符號語言（字母、含有字母的式子表示數量）的過程，體驗到數學符號作為解題工具所體現的優越性，從而培養學生的符號意識。

數學課程標準指出：“數學是刻畫自然規律和社會規律的科學語言和有效工具。”數學語言主要包括文字語言、圖形語言、符號語言，數學解題的本質就在于實現三種語言之間的相互轉化。正確靈活地運用文字語言、圖形語言和符號語言之間的轉化可以更快地厘清題意、明確思路，從而達到事半功倍的效果。

參考文獻

[1] 王國燦.新課標下小學數學閱讀能力的培養初探[J].新課程導學，2020（02）：39+46.

[2] 中華人民共和國教育部.義務教育數學課程標準（2022年版）[S].北京：北京師范大學出版社，2022.

[3] 謝學宙.小學生數學閱讀能力的培養途徑[J].天津教育，2020（16）：69-70.

[4] 陳婷，李蘭，蔡金法.中國小學數學“問題提出”教學的研究與實踐——基于《小學數學教師》和《小學教學》（數學版）中“問題提出”文章的分析[J].數學教育學報，2021，30（01）：19-24.

[責任編輯：陳國慶]