例談化歸思想在初中數學解題中的應用

摘要：化歸思想作為一種最基本的數學思想，在初中數學解題過程中

普遍運用，其本質就是將繁瑣的問題化為簡單易操作的問題，將未知考點轉化為已知知識來解答的過程.本文從實數計算、方程或不等式（組）、函數探究、三角函數應用、幾何證明等方面結合具體實例進行分析說明，并在研究過程中指導學生應用化歸思想，提升其數學核心素養.

關鍵詞：初中數學；化歸思想；解題研究

化歸思想是一種將問題由困難轉化為容易，由繁瑣轉化為簡單的過程，也可以說是轉化與歸一的總結.化歸思想在初中數學教學中經常涉及，在平時的解題過程中也都能體會到化歸思想的重要性.

1化歸思想的本質特點

化歸思想是學生在解決數學問題時常用的一種思想方法，其本質就是在解決問題過程中，把需要解決的問題通過已知知識進行轉化，歸結形成另一個比較簡單的問題，或是可以用已學知識解決的問題，這樣就可以通過解決這個簡單或利用已知知識能解決的問題達到解決原始

問題的目的.［1］歸根到底化歸的實質就是轉化.

2化歸思想在數學解題過程中的具體應用

化歸不僅是初中數學中一種重要的解題思想，也是一種問題突破的最基本思維策略，更是一種問題研究過程中有效的數學思維方式.［2］因此在解題過程中使用化歸思想進行分析研究，解答問題會取得意想不到的效果.

2.1化歸思想在實數計算過程中的應用

以人教版《義務教育教科書數學七年級上冊》第一章《有理數》教學為例，教師先引入“相反數”這個概念并把握“有理數的加法運算”，再學習“有理數的減法”，這就將減法問題轉化為已經熟悉把握的加法問題，學習了“倒數”知識點后，將有理數的除法運算轉化為乘法運算來解答，這樣難以表述的問題很自然地就可以解決了.正負數的減法就化歸為已經解決的正負數的加法了，而引入“倒數”這個概念后，正負數的除法就化歸為已經解決的正負數的乘法了.具體案例如下.

例1數學問題：計算12+122+123+124+…+12n（其中n是正整數，且n≥2）.

問題研究：直接計算上述問題，顯然對于七年級的學生來說很難，但是

轉化一下思想，將問題運用數形結合的思想方法，通過不斷地分割一個面積為1的正方形（如圖1），把問題中的數量關系和所分割的幾何圖形巧妙地結合起來，并采取一般問題特殊化的策略來進行探究，這個問題就容易解決了.

具體操作如下.第1次，分別連接各邊中點得到圖2，第2次，將圖2右下角正方形按上述方法再分割得到圖3，……，以此類推.當進行第n次操作后，將右下角最小正方形剪去，剩余圖形的面積是1-12n.

2.2化歸思想在方程或不等式（組）“消元”問題中的應用在計算一些特殊的方程或不等式（組）問題時，也是利用化歸思想將疑難方程進行轉化，將“多元”的轉化為“一元”的，將“特殊”形式轉化為“常規”形式進行解答.［3］例如，我們學習了一元一次不等式（組）的解法后，可以通過化歸思想來突破一元二次不等式的解法，以此解決后面的問題.具體案例如下.

例2解一元二次不等式x2-4＞0.顯然，這樣的問題已經遠遠超出學生的知識學習范圍，但是可以將整式x2-4進行分解因式，得x2-4＝（x+2）（x-2）.

∵x2-4＞0，∴（x+2）（x-2）＞0，再根據有理數的乘法法則“兩數相乘，同號得正”，得到式子x+2>0，x-2>0或x+2<0，x-2<0，這樣就將超綱問題轉化為學生可解問題，這種解一元二次不等式的過程，真正體現了數學的化歸思想.

2.3化歸思想在函數探究問題中的應用

在一些函數問題上也經常用到化歸思想，將不好把握的問題轉化為容易理解的問題進行處理，如函數與方程或不等式之間的關系，借助圖形將問題轉化，解答輕而易舉.［5］具體案例如下.

例3在平面直角坐標系xOy中，已知拋物線y＝ax2+bx經過A（4，0），B（1，4）兩點.P是拋物線上一點，且在直線AB的上方.如圖5所示，OP交AB于點C，PD∥BO交AB于點D.記△CDP，△CPB，△CBO的面積分別為S1，S2，S3.判斷S1S2+S2S3是否存在最大值.若存在，求出最大值；若不存在，請說明理由.

針對S1S2+S2S3是否存在最大值的問題，學生很難直接入手，但如果將面積問題轉化為線段之間的關系問題，學生就容易理解.如圖6所示，根據PD∥OB，可得△DPC∽△BOC，所以CP∶CO＝CD∶CB＝PD∶OB，從而發現S1S2=CDCB=PDOB，S2S3=CPCO=PDOB，此時發現S1S2+S2S3＝2PDOB，這樣只要再計算2PDOB的最大值即可將問題解決.

2.4化歸思想在三角函數問題中的應用

在三角函數的相關內容學習時，也常常出現角與邊之間的關系，利用化歸思想，很容易突破邊角關系，建立等式讓問題得解.具體案例如下.

例4某市要舉辦首屆旅游發展大會，該市積極優化環境.如圖7所示，規劃中的一片三角形區域需美化，已知∠A＝67°，∠B＝53°，AC＝80米，求這片區域的面積.（結果保留根號.參考數據：sin53°≈0.8，sin67°≈0.9）

根據題目的條件，學生無法進行正常計算，但是考慮到問題涉及三角函數，需要進行添加輔助線，構造直角三角形.在△ABC中，∠A，∠B，∠C所對的邊分別為a，b，c，如圖8所示，過點C作CD⊥AB于點D，則在Rt△BCD中，CD＝asinB，在Rt△ACD中，CD＝bsinA，∴asinB＝bsinA，可得asinA＝bsinB，據此，可以轉化得到三角形三邊與三角函數值的關系，從而借助上述關系求得

AE，BC的值，即可得到S△ABC的大小，問題得以解決.

2.5化歸思想在幾何證明過程中的應用以人教版《義務教育教科書數學九年級上冊》中關于“圓”部分內容為例，在研究分析“同弧所對的圓周角的度數等于這條弧所對的圓心角的度數的一半”的過程中，將問題分為三種情況：①當點O的位置在圓周角的一條邊上（如圖9）；

②在圓周角的內部（如圖10）；③在圓周角的外部（如圖11）.

教材根據第一種情況可以利用外角性質直接得到答案，但是對于后面兩種情況，卻要求學生自己研究解決.

面對這樣的問題，很多同學在分析時找不到思路，其實是忽略了化歸思想的運用，既然第一種方法如此簡單，就可以將第二種、第三種情況分別轉化為第一種問題的模式上來，從而連接點C與點O，形成直徑，再利用第一種情況的解法順利解答.

在幾何圖形求解陰影面積等方面，化歸思想也經常體現其中.具體案例如下.

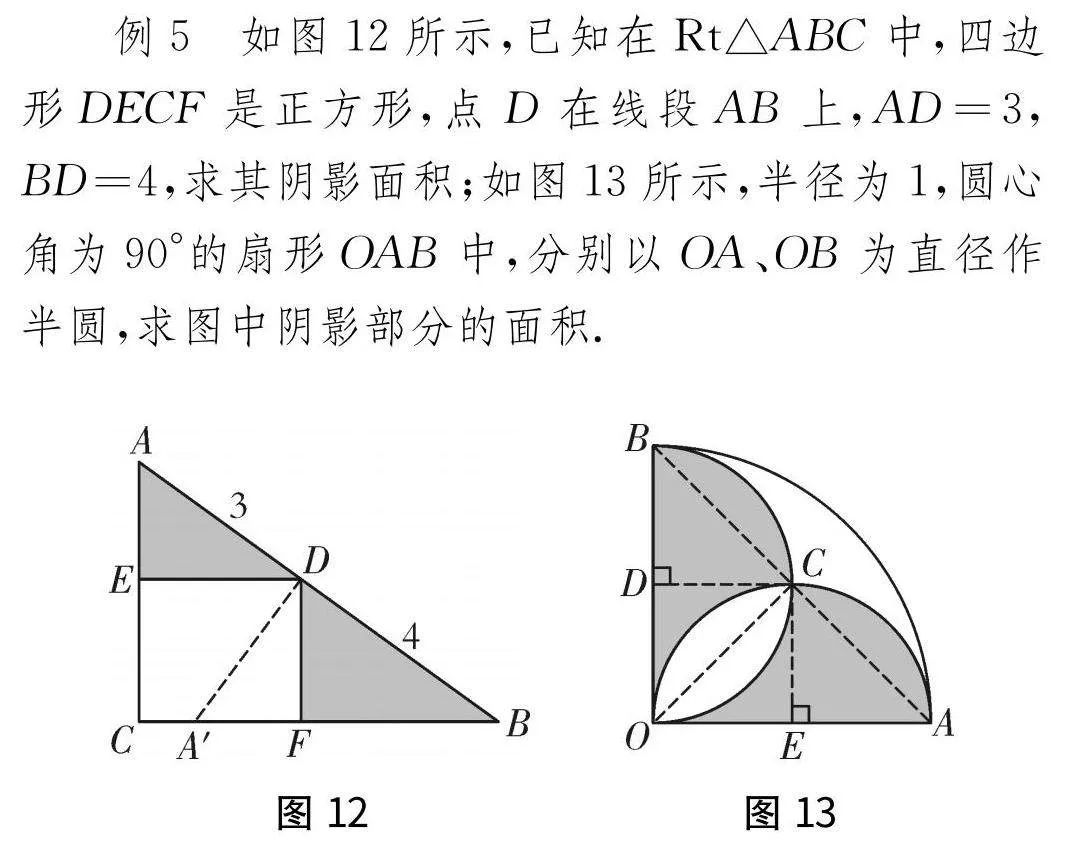
例5如圖12所示，已知在Rt△ABC中，四邊形DECF是正方形，點D在線段AB上，AD=3，BD=4，求其陰影面積；如圖13所示，半徑為1，圓心角為90°的扇形OAB中，分別以OA、OB為直徑作半圓，求圖中陰影部分的面積.

像這樣的陰影面積問題，學生直接去求各個部分的面積往往計算量大或者繁瑣，但是

在問題的特點基礎上可以利用化歸思想，將不規則的圖形轉化為規則的圖形，解起來就非常簡單，如圖12中可以添加DA′這樣一條輔助線，通過旋轉將兩個直角三角形轉化為一個直角三角形即可求解.扇形問題通過分割將不規則的扇形填補形成一個等腰直角三角形，問題也很容易求解.

當然，在研究其他類型的幾何圖形證明過程中，同樣可以借助題干中的情境進行轉化，將問題轉化為圖形或者思維導圖等方式進行解答，這樣的化歸思想能夠將問題直觀化.思路顯性化，很容易找到問題的突破.

3結語

綜上所述，化歸思想在初中數學解題中有重要意義，把握化歸思想的本質特點，善于從問題的情境中獲取相關信息，進行等價轉化，從而很容易將疑難問題化解.

［5］有了這種思想可以減輕學生對數學難題的恐懼感，也能輕而易舉地找到問題的突破口隨著新課程標準的實施，數學問題也不斷向思維深度發展，教師在教學過程中更要注意化歸思想的灌輸與引導，讓學生充分地把握其內涵，并在訓練中靈活運用，從而達到提高數學思維能力，提升數學核心素養的最終目的.

參考文獻

［1］秦艷萍.化歸思想在三角函數解題中的應用［J］.數理天地（高中版），2022（15）：64-65.

［2］顏艷.滲透轉化與化歸思想 培養數學核心素養［J］.考試周刊，2021（78）：85-87.

［3］聶佑林.把握數學本質，重視化歸滲透［J］.中學數學教學參考，2021（31）：50-52.

［4］王賽楠.轉化思想在初中數學解題中的具體應用［J］.初中數學教與學，2022（7）：22-23+47.

［5］王學信.化歸思想在初中數學教學中的滲透研究［J］.課程教育研究，2018（17）：156.