老教師與年輕教師的一節課

【摘要】文章以“平面直角坐標系”一課為例,通過觀摩本校老教師鄒老師的課堂教學,并與自己入職第一年的課堂教學進行對比,從復習引入、新課教學、知識運用、課堂小結四個方面進行分析,談談自己的體會和對教學的啟示。
【關鍵詞】初中數學;對比教學;平面直角坐標系
當今快速發展的社會對人才的要求更高,作為培養新時代少年的年輕教師,更要與時俱進并踐行終生學習的理念。
一、教學過程的對比與分析
1.復習引入環節的教學對比
(1)鄒老師的課堂教學片斷。
師:我們前面學習了數軸,數軸包含三要素,分別是什么?生:原點、方向、單位長度。
師:我們為什么要學習數軸,它給我們研究數學帶來什么好處呢?(一系列問題串)生A:數軸上的點可以表示數,且與實數一一對應。生B:利用數軸可以方便比較數的大小。生C:數軸還可以確定兩點間的距離和數的絕對值。生D:數軸還可以表示不等式、不等式組的解集。
師:非常好,那么生活中我們是如何確定物體位置的呢?比如棋子,電影院的座位。一個數還夠嗎?生E:必須兩個。
師:什么給你的啟示?生E:電影票。
師:五排六列和六列五排是一個位置嗎?生E:不是。
師:也就是說這數對是有順序的,那么給你一個平面,如何確定一個點的位置呢?生F:兩個數軸。
師:兩個數軸就會有兩個原點,兩個正方向,兩個單位長度,那么該怎么畫呢?生F:兩個數軸要互相垂直,同一個原點,同一個單位長度。
師板書,畫一個直角坐標系。
(2)筆者的課堂教學片斷。
筆者:同學們我們前面已經學習了數軸,什么是數軸?生:規定了原點、方向、單位長度的直線。
筆者:很好,我們還知道數軸上的點和實數是一一對應的,那么平面上的點該如何表示呢?請大家思考生活中的事例,隊列中的戰士、電影院的座位、教室里的學生。我們都是通過排和列來描述的,也就是說要有兩個數,并且這兩個數是有順序的。兩排三列和三排兩列是不一樣的。我們也可以借助這種“有序數對”來表示平面內的點。這就是今天我們要學習的平面直角坐標系。
(3)對比分析。鄒老師通過三個主要問題,不僅復習了舊識,引出了新知,更重要的意義在于溝通了新舊知識之間的內在聯系,并為本節課的教學構建了一個好的框架。學生可以用同樣的模式研究坐標系,即以類似的三個問題進行思考。而筆者的教學過程并沒有對數軸進行深入的復習,僅僅是表面上的復習,顯然對學習本課幫助不大。并且筆者在課堂上以講為主,沒有充分發揮學生的主觀能動性。
2.新課教學部分的對比
(1)鄒老師的課堂教學片斷。
師:點P除了用數對(4,3)表示外,還可以有其他數對來表示它嗎?(停頓、引導)生:沒有,因為過一點有且只有一條直線與已知直線垂直。
師:很好,那反過來,數對(4,3)除了表示點P外,是否還會表示其他的點?生:不會,兩條直線相交有且只有一個交點。
師:非常好,對于平面內的任意一點P可以確定唯一一個有序實數對(a,b),反過來有序數對(a,b)也可以唯一確定一點。也就是說平面內的點與有序實數對一一對應的,我們將有序實數對稱為點的坐標。確定點的坐標同學們要注意,先垂線,后垂足,找出有序實數對,先橫后縱再括號,中間隔開用逗號。
(2)筆者的課堂教學片斷。
筆者:一般地,對于坐標平面內的任意一點P,過點P作x軸的垂線,垂足為M,可得點M在x軸上所對應的實數a;再過點P作y軸的垂線,垂足為N,可得點N在y軸上所對應的實數b,那么有序實數對(a,b)表示點P,因為過一點作已知直線的垂線能且只能作一條,所以這樣的有序實數對是唯一確定的……
(3)對比分析。對于知識點“平面內的任一點都有唯一的有序實數對與之一一對應”的歸納,鄒老師放手讓學生思考回答,在課堂上就有一位學生給出了非常完美的答案。而筆者的課堂只是按照板書講解,并沒有給學生思考的時間和表達的機會。
3.新知運用部分的教學對比
(1)鄒老師的教學設計。
課堂教學片段:
師:點E的坐標是?生:-4。
(有質疑聲)
師:好像有不同意見,你再好好想一想我們是如何確定點的坐標的?把機會留給你,再試一試吧。生:(-4,0)。
師:你是怎么做的?生:先向Pyem6orQAsgWRew9YjeDCqSY95CjOIjFQm6qaA3rNFU=x軸作垂線,對應-4。再向y軸作垂線對應0。
師:嗯,非常好,經過自己的努力,把這問題解決了。
(2)筆者的課堂教學設計。
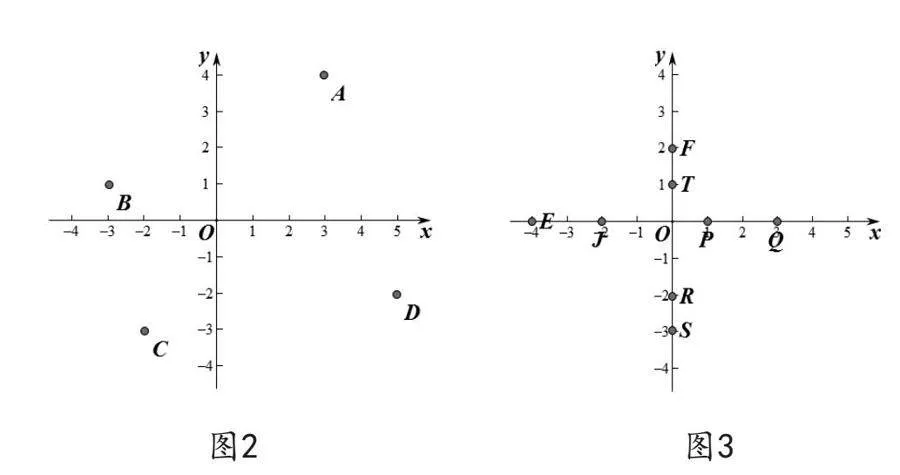
例1:寫出圖2中直角坐標平面內各點的坐標。
例題2:寫出圖3中坐標軸上各點的坐標。
(3)對比分析。例題的設計,鄒老師巧妙地將課本中例1和例2合二為一,并將B點稍做改動。由特殊到一般,學生更容易理解接受。在對比的過程中,也加強了學生對點坐標的確定方法,理解坐標的有序性。筆者在例2中多設計了幾個坐標軸上的點,學生更容易發現坐標軸上點坐標的特征。
4.課堂小結環節的教學對比
(1)鄒老師的教學設計。
三個問題:學什么?怎么做?為什么學?并提供故事和寄語。
(2)筆者的教學設計。
平面直角坐標系:①坐標軸:橫軸(x軸),縱軸(y軸),坐標原點。②直角坐標平面內的點與有序實數對建立一一對應關系。③點的坐標,點的坐標表示方法,P(a,b)。④x軸上點的坐標是(x,0);y軸上點的坐標是(0,y);坐標原點的坐標是(0,0)。
(3)對比分析。鄒老師的小結給筆者耳目一新的感覺,學生以三個問題為依據進行小結歸納,并且小結又分三個層次。而筆者僅僅停留在本節課的知識層面,沒有體現知識之間的聯系和發展。
二、思考和啟示
1.復習引入——關注新舊知識之間的聯系
通過復習引入符合學生的認知規律。通過復習,建構起新舊知識之間的橋梁。學生在復習回顧的過程中,能夠進一步掌握舊知識或者解決問題的方法,為學習探究新的知識做好準備。
2.新課教學——關注知識的生成過程
日常教學要以知識的生成、發生、發展為主線,重視基本數學概念的抽象,數學公式、解題方法的概括總結、歸納推導過程,把課堂還給學生,做到以學生為主體。
3.新知運用——關注練習設計的多樣化和層次性
數學課堂中練習是不可或缺的。圍繞教學目標,側重教學重難點,設計多樣化、有層次的題目。形式多樣化,獨立完成,小組合作完成。有時也可以采取游戲的方式,這既可鞏固知識,又能提高學生的學習興趣。
4.課堂小結——關注知識的系統性
課堂小結不能僅僅局限在一節課的知識層面,更重要的是注重知識間的聯系。通過小結,搭建知識框架,建立知識體系,為學生的后續發展打下堅實的基礎。
【參考文獻】
[1]中華人民共和國教育部.義務教育數學課程標準(2022年版)[S].北京:北京師范大學出版社,2022.

