整體命制 分層檢測 分類補償

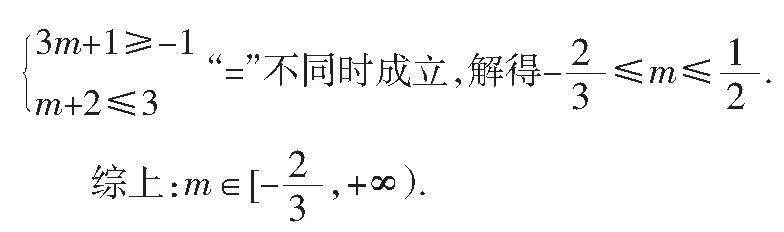
摘 要：檢測是實現教學診斷與學習糾錯的重要載體，也是教學反饋與學習效果評價的重要依據.精準依據教學目標命制分層檢測是實現教學診斷的前提，科學分析檢測數據命制分類補償練習是實現學習糾錯的重要抓手.

關鍵詞：診斷;糾錯;檢測;命制;評價

在數學教學中，檢測是評估學生學習效果、發現教學問題的重要手段.要使檢測真正發揮診斷與糾錯功能，需關注精準命制與講課補償.利用本校教研組活動機會，提供兩道數學檢測題給教師解題析題與學生測試.下面依據本校師生實測的結果，從檢測題的答案解析、檢測題命制、檢測題講評三個視角進行分析與探討，如何讓檢測更好地實現診斷與糾錯功能.

1 試題與解析

題目1 設集合A=x│-1≤x≤2，集合B=x│2m<x<1.

若x∈ A是x∈ B的必要條件，求實數m的取值范圍.

解析 ：由x∈ A是x∈ B的必要條件，則B?A，又A=x│-1≤x≤2，

題目2已知命題p：x<-1或x>3，命題q：x<3m+1或x>m+2.

若p是q的充分非必要條件，求實數m的取值范圍.

2 師生解答與分析

2.1 教師解答及分析

教研現場收回有效答卷20份，經整理分析教師解答的思路主要如下.

教研意圖：對集合=x│x<3m+1或x>m+2表達數集數學地準確理解，能夠分類討論集合可能表達的數集進行全面考慮，可與題目1形成空集與全集完整的知識結構.

2.2 學生解答及分析

題目1與題目2知識相近、方法相似、考法相同，但正確率卻差異懸殊.為了進一步了解原因，把兩道檢測題發給兩個高一平行班，用時20分鐘收回有效答卷100份（共101人），經整理分析學生解法的思路主要如下.

檢測意圖：檢測學生對充分非必要條件理解與運用及命題q表達數集的情形討論，可與題目1形成解法遷移.

從實測效果，不管是學生層面還是教師層面來看，以上題目沒有達到命題與檢測的目的.這引發了如下思考，如何命制能準確呈現診斷效果的檢測題，以及檢測診斷出問題后如何進行講評并設計變式補償練習實現糾錯效果.讓學生動起來，讓學習高效，是每一位教師直面的現實問題.

3 教學思考

3.1 精準依據教學目標命制分層檢測題

美國著名的數學問題解決專家匈菲爾德，給出了所謂“好問題”的五條審美原則，即一個好問題必須：（1）是容易接受的，不需要大量的技巧;（2）有多種解題方法或者至少有多種思路;（3）蘊含了重要的數學思想;（4）不故意設陷阱;（5）可以進一步開展和一般化，引發豐富的數學探索活動.好問題能夠把學生引向真正的、誠實的、有價值的數學.也就是說，不僅問題本身是有價值的，通過它們，學生能有所進步，能獲得重要的數學思想，而且解決問題涉及的推理模式也同樣具有價值.它既反映了一般的、有用的數學思維模式，也能為運用特殊的探索策略提供良好的素材.好的問題應該成為豐富的數學探索活動的起點，給學生“做數學”的機會.

因此，在命制檢測題時盡量采用大題小問、適度搭梯、分層設置的方式進行.為了更好地體現檢測題的效果，把題目1改編成變式1，把題目2改編成變式2，供年級周測使用.經實測反饋效果良好，實現了預期的診斷功能，并達到了既定的診斷目的.

變式1 設集合A=x│-1≤x≤2，集合B=x│2m<x<1.

（1）若A∩B=Φ，求實數的取值范圍.

（2）若“x∈A”是“x∈B”的必要條件，求實數m的取值范圍.

變式2 已知命題p：x<-1或x>3，命題q：x<3m+1或x>m+2.

（2）若p是q的充分非必要條件，求實數的取值范圍.

命題意圖：以一題多問的方式對檢測題進行分層設置，既重視基礎性考查又重視思維品質的多維考查，讓不同的學生在試題的解答中實現分層，從而實現檢測題的診斷功能.

3.2 科學分析檢測數據命制分類補償練習

教師的解題思維與學生的解題思維呈現正相關關系，在檢測題講評中要充分暴露教師的思考問題的過程，讓學生充分理解解題思維的自然形成過程，解題方法實現正遷移.在檢測中發現問題并進行診斷后，需要通過檢測題的講評，聚焦學生的薄弱環節，設計有針對性的變式作業與檢測題，進行變式補償訓練，幫助學生形成知識體系、遷移解題方法，提升解決問題的能力，發展數學素養.年級周測后針對學生答題實際，參照變式1與變式2檢測題，再設計變式3與變式4補償練習題，供年級檢測題講評后學生練習.后經評改反饋，95%以上的學生均能正確完成，收到了檢測題評析糾錯的效果.

變式3 已知集合A=x│（x+2）（x-5）≤0，B=x│m+1≤x<2m-1.

設計意圖：變式補償作業與檢測題構成知識體系，強調對知識全面的考查，建構知識單元與解決同類問題方法的正遷移，讓大部分同學在檢測題講評后通過變式補償作業達到糾錯的學習效果.

數學學科核心素養是數學課程目標的集中體現，是在數學學習的過程中逐步形成的[ 1 ].學生數學學科核心素養水平的達成不是一蹴而就的，具有階段性、連續性、整合性等特點[ 1 ].“雙減”大背景下的數學檢測題內容改革，對數學教學產生積極的影響，命制檢測題時遵循大題小問、適度搭梯、分層設置，檢測題講評中充分呈現解題思維的生成過程，檢測題講評后設計有針對性的變式作業進行補償糾錯，著力構建層次分明、循序漸近的數學課堂，學生的素養就會在課堂中自然而然的蘊育生長，檢測題的診斷與糾錯功能就能水到渠成.

參考文獻：

[1] 中華人民共和國教育部.普通高中數學課程標準（2017版2020年修訂）[S].北京：人民教育出版社，2020：4，81.