淺析泰勒公式在高中數學的應用

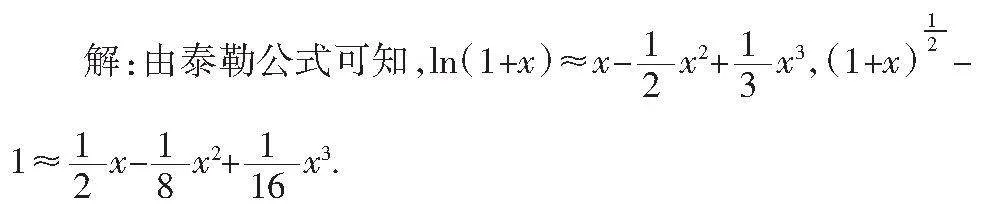
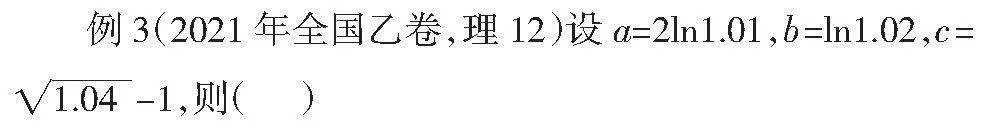
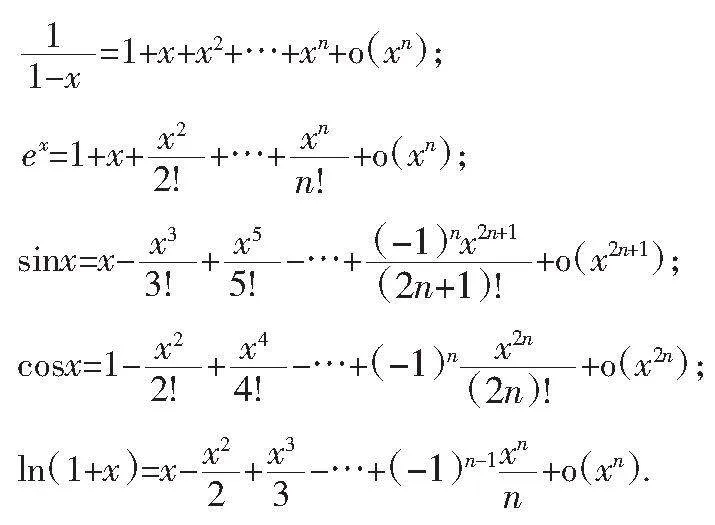
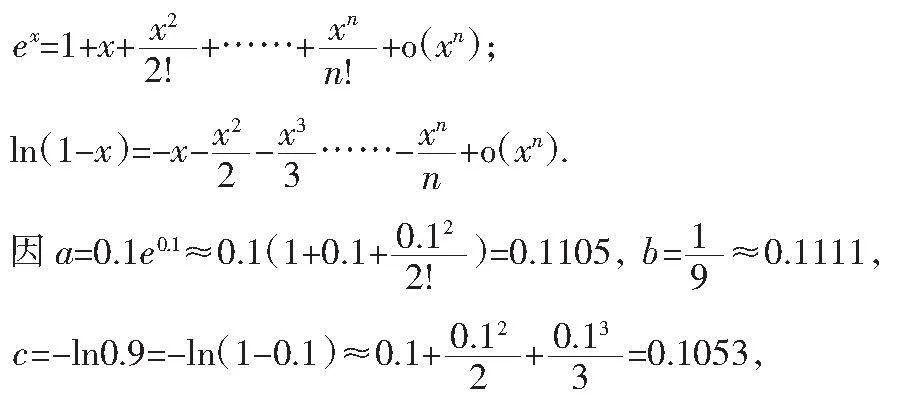
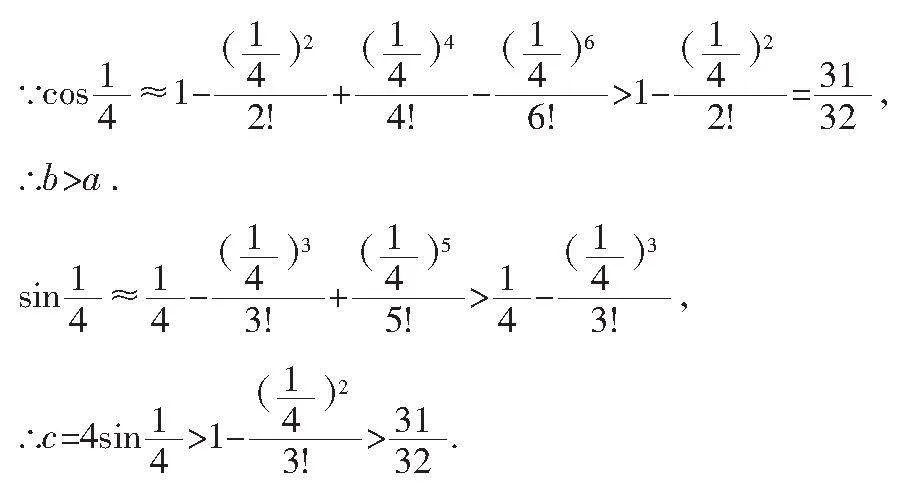
摘 要：泰勒公式是現代數學分析的重要內容，在研究和分析各種數學問題中有著重要的作用，其理論是研究函數極限和估計誤差等方面的重要工具.近幾年來高考的熱門題型比較大小，一般是先構造模型，然后代入數值運算及比較.學生往往在選擇函數模型方面有一定的難度.靈活正確地使用泰勒公式，可以使得解題更加方便，達到事半功倍的效果.探討泰勒公式在高考試題等知識領域的應用有助于學生拓展思維、鍛煉能力.

關鍵詞：泰勒公式;比較大小;高中數學

泰勒公式是數學分析中一個非常重要的內容，其基本思想是用多項式逼近已知的函數，而這個多項式的系數一般由給定函數的各階函數導數確定.它是研究函數極限與估計誤差等方面的重要工具[ 1 ]，正確利用泰勒公式來解決相關問題，可以達到事半功倍的效果.近幾年高中數學函數問題解決過程中應用泰勒展開式案例頗多.學習泰勒公式，并能學以致用可以更便捷解決函數類相關問題[ 1 ].

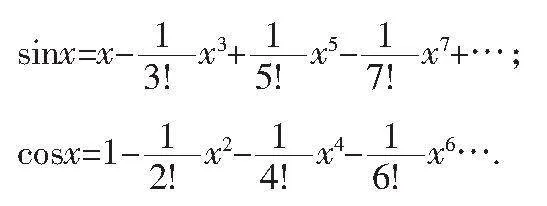
1 常用函數的泰勒展開式

首先，了解泰勒展開式是將一個在x=x0處具有n階導數的函數f（x）利用關于（x-x0）的n次多項式來逼近函數的方法[ 2 ].

1.1高中數學學習中，面對復雜的函數問題時，常用函數泰勒展開式有以下幾個：

2 泰勒公式在近年高考試題中的應用

2.1 教材中的應用

在人教版《普通高中教科書·數學》必修第一冊A版（2019年版本）中第五章《三角函數》復習參考題5第26題，英國著名的數學家泰勒發現了三角函數拓展公式：

運用泰勒公式在一些求具體函數實際數值時（尤其是當項數比較少時函數取值）計算很方便.

2.2 高考中的常用泰勒展開式及其應用

泰勒公式是高等數學的知識，在高中數學學習中適時拓展應用，可以起到事半功倍的效果.在高中數學命題中的常用模式：（1）從泰勒公式的本身內涵及其一般常用結論來設計題目.對于這類題目的命制，要求命題人在命題時必須對泰勒公式的內涵全面深入了解，然后提煉出與中學數學相掛鉤的常用函數.從泰勒公式一般結論出發，常考慮近似取值前幾項，通過逆推和具體化來命題，將泰勒公式進行簡化和近似取值，并進行四則運算.（2）直接套用泰勒公式展開式進行題目命題.這類題目可以直接用泰勒公式近似取值，檢驗結果是否正確[ 2 ].

高考中的常用泰勒展開式有：

從以上案例歸納出，對任意函數進行泰勒展開，并不一定用到f（x）的具體表達式，而結論往往是一般性的，試題的命制者出發點和思考點是奠定在綜合思維基礎上，將平時常用一般性的結論引進到某些特定函數之中，然后構造得到一些結構整齊勻稱的式子.這類題目是多重思維的疊加，綜合考察學生的創新思維能力，通常起到高考選擇題、填空題的壓軸作用[ 3 ].對大部分學生來說此類試題是陌生的，與他們平時訓練的題目有所不同，非常規思路.這會使大部分學生感到困難，無從下手，束手無策，尤其在考試中有一定的壓力.而解決這類問題只要學生平時多了解一些泰勒公式的應用，通過放縮等方法，比較兩個式子的大小，也就迎刃而解.

2.3 高考真題案例分析

A、a<b<c B、c<b<a C、c<a<b D、a<c<b

分析：從已知條件的中，選擇常用函數泰勒展開式得知

從以上分析中得c<a<b. 故選：C.

A、a<b<c B、b<c<a C、b<a<c D、c<a<b

分析：從已知條件的中，選擇常用函數泰勒展開式得知

從以上分析中得： a<b<c. 選A.

A、a<b<c B、b<c<a C、b<a<c D、c<a<b

將x=0.01，x=0.02，x=0.04代入以上泰勒公式即可得a，b，c值，

易得b<c<a. 故選：B.

由以上三個例子分析可知，泰勒公式在估值方面（尤其項數取值比較少時）一般非常準確，所以，在碰到幾個超越函數比較相近又一時無從下手時往往可以考慮運用泰勒公式.不難看出，泰勒公式在比較大小這類問題時，起著非常重要的作用，教師在高中實際教學中可以借助課后習題或平時拓展知識引入一些泰勒公式的知識，拓展學生思維，提升學生思維能力，引發學生學習興趣.

總之，利用泰勒公式對求解一些難度比較大的試題可以起到事半功倍的效果.利用泰勒公式前提是抓住函數的基本特征，靈活合理構造函數.在構造函數時，盡量不用除式，多用乘積表達逐步引入泰勒公式進行估計，在讓學生了解估計與計算這類近似問題時會很方便，而且對于我們研究某些具體函數會起到一定的指導作用.近年高考中，比較喜歡考查的是比較實數大小，此時考慮運用泰勒公式可以很快解決問題.這類問題一般出現在選擇題或填空題，常見的泰勒展開式也可以運用于解決證明題或者是導數大題[ 3 ].

3 價值取向

近年來，在各級各類考試和高考命題中，命題者都很喜歡不等式ex≥x+1，lnx≤x-1的應用，上面的不等式可以利用圖像說明結論.追其根本，這兩個不等式在某種程度上都來源于高等數學中的泰勒展開式，在高等數學中，泰勒公式利用函數在某點的信息，描述其附近取值的公式.如果函數連續且平滑，那么泰勒公式可用這些導數值作為系數構建一個多項式.

向量、導數、概率統計等等以前在大學才能接觸到的知識點，已經以探索、拓展、提升等形式滲透進新教材、新高考.高考這一極其重要的選拔人才的考試中，高等數學常常作為高考命題出發點，考查學生的知識遷移能力，綜合分析問題能力以及應用能力.培養并提高學生的創新思維，不僅要讓學生對各種常規題型、基礎題型等加以訓練，還要培養學生換位思考問題的能力，努力站在命題者的角度去考慮問題[ 4 ].高中教師要用新課程標準審視常規教學，不斷地提高教研能力.

參考文獻：

[1] 孔珊珊. 泰勒公式在數值計算中的應用[J].濟寧學院學報，2011，32（3）：70-72.

[2] 潘勁松. 泰勒公式的證明及應用[J].廊坊師范學院學報，2010，10（2） ：16-21.

[3] 陳炳泉. 一道高考導數題的思考與探索[J].數學通報，2021，60（3）：59-62，66.

[4] 陳炳泉. 基于數學核心素養的高考一類常見導數題思考與探索[J].福建中學數學，2023（4）：45-48.