高二期末創新模擬卷(2)

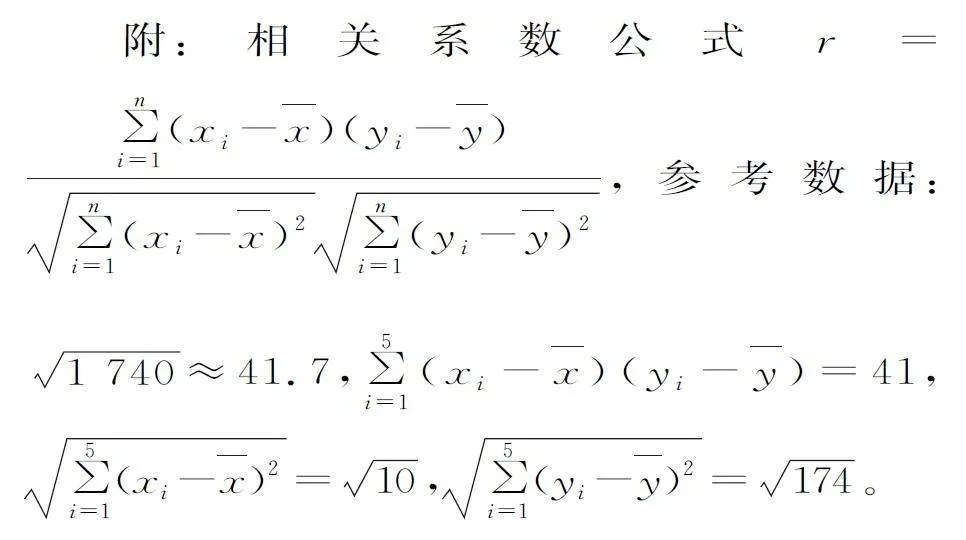
一、單選題（本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

1.2024 年賀歲片《第二十條》《熱辣滾燙》《飛馳人生2》引爆了電影市場，小明和他的同學一行四人決定去看這三部電影，每人獨立決定看其中的哪一部，則恰有兩人看同一部影片的選擇共有（ ）。

A.9種 B.36種

C.38種 D.45種

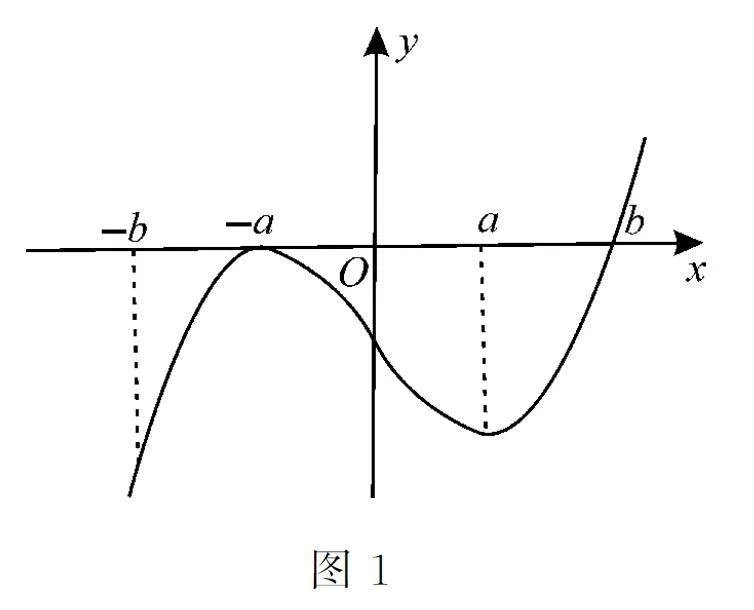
2.函數y =f（x）的導函數y=f'（x）的圖像如圖1所示，則下列說法中正確的是（ ）。

A.x=a 是函數y=f（x）的極小值點

B.當x=-a 或x=b 時，函數y=f（x）的值為0

C.函數y=f（x）在（a，+∞）上是增函數

D.函數y=f（x）在（b，+∞）上是增函數

3.用模型y=aekx 擬合一組數據組（xi，yi）（i=1，2，3，…，7），其中x1+x2+…+x7=14，設z=ln y，得到變換后的線性回歸方程為^z=x+1，則y1y2…y7=（ ）。

A.e35 B.e21 C.35 D.21

4.已知ξ 服從正態分布N（2，σ2），a∈R，當P（ξ>a）=0.5時，關于x 的二項式 （ax+1／x2 ）3的展開式的常數項為（ ）。

A.1 B.4 C.6 D.12

5.用2個0，2個1和1個2組成一個五位數，則這樣的五位數有（ ）。

A.8個 B.12個

C.18個 D.24個

6.中國南北朝時期的著作《孫子算經》中，對同余除法有較深的研究。設a，b，m（m>0）為整數，若a 和b 被m 除得的余數相同，則稱a 和b 對模m 同余，記為a≡b（mod m）。若a=C0 20+C1 20×3+C2 20×32+…+C20 20×320，a≡b（mod 5），則b 的值可以是（ ）。

A.2 004 B.2 005

C.2 025 D.2 026

7.函數的凹凸性是函數的重要性質之一。函數凹凸性的定義：函數y=f（x）在區間（a，b）內可導，x0 是（a，b）內任一點，若曲線弧上點（x0，f（x0））處的切線總位于曲線弧的下方，則稱曲線弧在（a，b）內是凹的;若曲線弧上點（x0，f（x0））處的切線總位于曲線弧的上方，則稱曲線弧在（a，b）內是凸的。函數f （x）在區間上為凹（凸）函數等價于f（x）的導函數在區間上單調遞增（遞減）。若f（x）=mex -x3 +1在定義域內是凹函數，則m 的最小值是（ ）。

A.-6e B.6／e

C.12／e2 D.12／e3

8.設a=ln（1+0.1），b=sin 0.1，c=2／21，則下列大小關系正確的是（ ）。

A.a<b<c B.a<c<b

C.c<a<b D.c<b<a

二、多選題（本題共3小題，每小題6分，共18分。在每小題給出的四個選項中，有多項符合題目要求。全部選對得6分，部分選對的得部分分，有選錯的得0分。）

9.下列說法正確的是（ ）。

A.若數據1，3，4，4，m 的極差和平均數相等，則m =17／4

B.數據1，3，7，7，9，12，16的第80百分位數為10.5

C.已知y 關于x 的回歸直線方程為^y=0.3-0.7x，則樣本點（2，-3）的殘差為-1.9

D.若X ～B（ 4，2／3），隨機變量Y=3X -1，則E（Y）=7

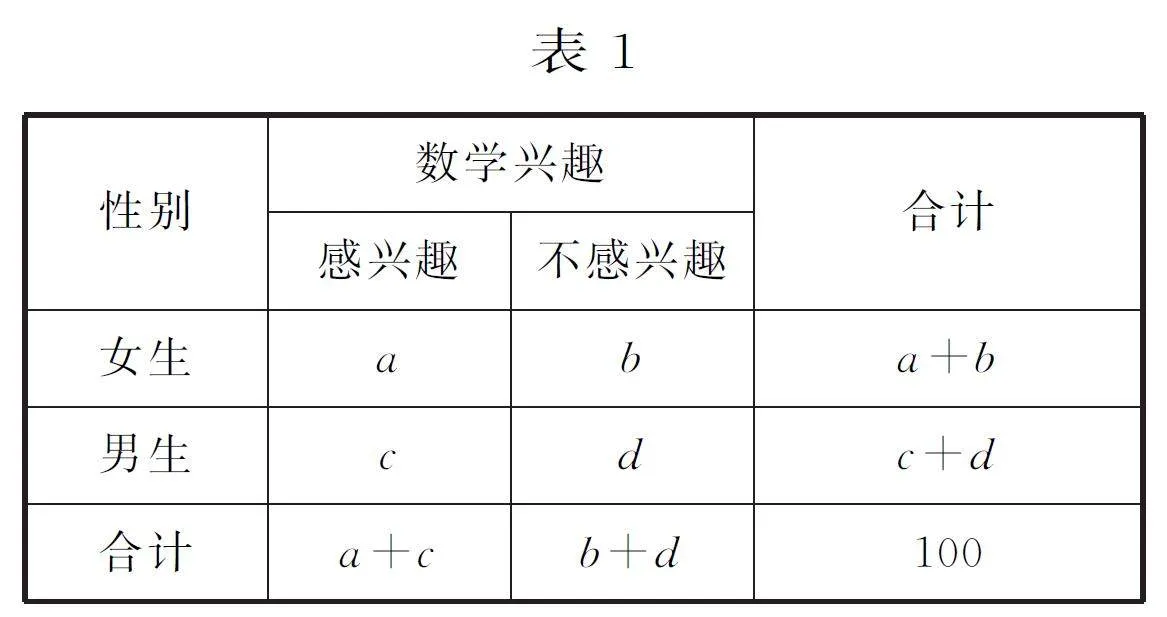
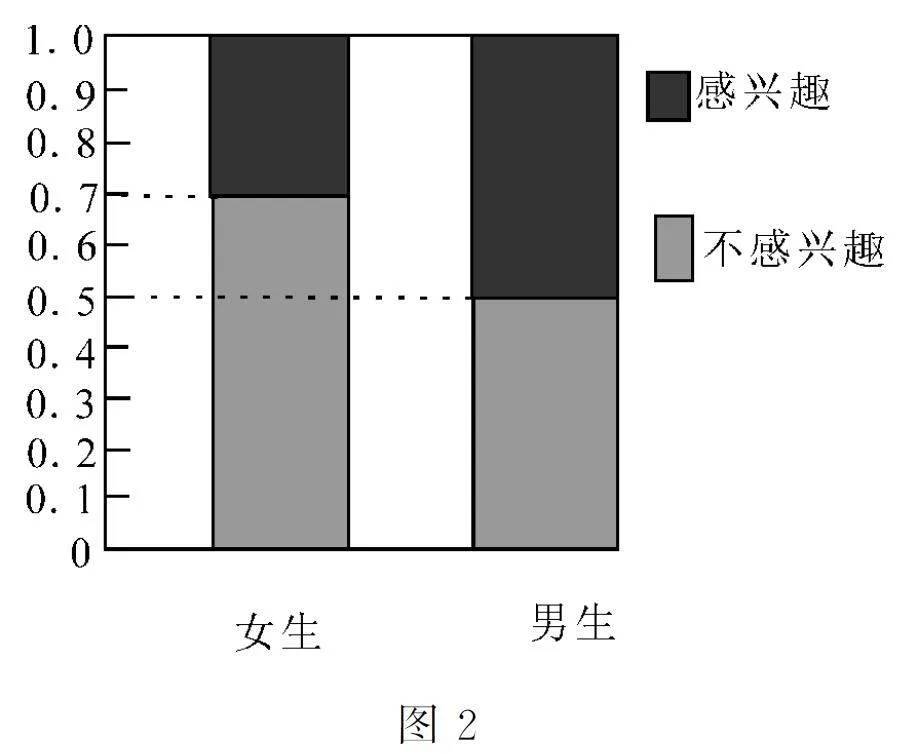
10. 某校為了解高一新生對數學是否感興趣，從400名女生和600 名男生中通過分層抽樣的方式隨機抽取100名學生進行問卷調查。由調查的結果得到如圖2所示的等高堆積條形圖和如表1所示的列聯表，則（ ）。

參考數據： 本題中χ2 =n（ad-bc）2／（a+b）（c+d）（a+c）（b+d）≈3.936。

A.表中a=12，c=30

B.可以估計該校高一新生中對數學不感興趣的女生人數比男生多

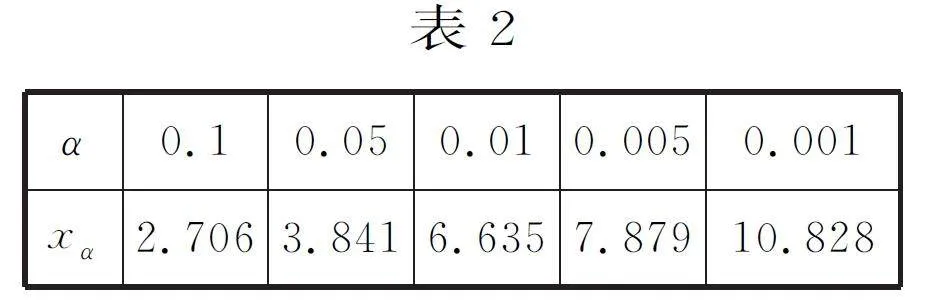
C.根據小概率值α=0.05的χ2 獨立性檢驗，可以認為性別與對數學的興趣有差異

D.根據小概率值α=0.01的χ2 獨立性檢驗，可以認為性別與對數學的興趣沒有差異

11.若關于x 的不等式ex-2 +x ≥2ax2-xln x 在（0，+∞）上恒成立，則實數a的值可以是（ ）。

A.1／e B.1／2

C.根號e／3 D.2

三、填空題（本題共3小題，每小題5分，共15分。）

12.已知（x +2）4 （2x2 +3x）=a0 +a1x+a2x2+…+a6x6，則a4=____。

13.在數學中，有一個被稱為自然常數（又叫歐拉數）的常數e≈2.718 28。小明在設置銀行卡的數字密碼時，打算將自然常數的前6位數字2，7，1，8，2，8進行某種排列得到密碼。如果排列時要求兩個2相鄰，兩個8不相鄰，那么小明可以設置的不同密碼共有____個。

14.甲、乙兩同學玩擲骰子游戲，規則如下：

（1）甲、乙各拋擲質地均勻的骰子一次，甲得到的點數為n1，乙得到的點數為n2;

（2）若n1 + n2 的值能使二項式（2x+1/x）n1+n2的展開式中第5 項的二項式系數最大，則甲勝，否則乙勝。

那么甲勝的概率為____。

四、解答題（本題共5小題，共77分，解答時應寫出文字說明、證明過程或演算步驟。）

15.（本小題13 分）已知函數f （x）=ax2-（a+2）x+ln x。

（1）若x=1是函數f（x）的極值點，求f（x）在區間[1/2，2] 上的最值;

（2）若g（x）=ax2 -2x +ex，f （x）≤g（x）恒成立，求實數a 的取值范圍。

16.（本小題15分）如圖3，一個質點在隨機外力的作用下，從數軸點1的位置出發，每隔1 s向左或向右移動一個單位，設每次向右移動的概率為p（0<p<1）。

（1）當p=1/2時，求5 s后質點移動到點0的位置的概率;

（2）記3 s后質點的位置對應的數為X ，若隨機變量X 的期望E （X ）>0，求p 的取值范圍。

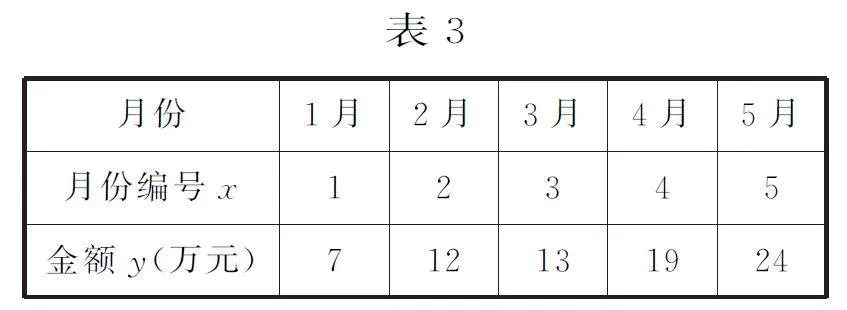
17.（本小題15分）直播帶v/iYJwrmdt529Y0kgQ+fgw==貨是一種直播和電商相結合的銷售手段，目前已被廣大消費者所接受。針對這種現狀，某公司決定逐月加大直播帶貨的投入，希望直播帶貨金額穩步提升。該公司2024年前5個月帶貨金額的統計表如表3所示（金額y（萬元））。

（1）根據統計表：

①求該公司帶貨金額的平均值y;

②求該公司帶貨金額y 與月份編號x 的樣本相關系數9BoJVLqX/9Id3C/6Dj5zeA==（精確到0.01），并判斷它們是否具有線性相關關系。（當0.75≤|r|≤1時，認為y 與x 的線性相關性較強;當|r|<0.75時，認為y 與x 的線性相關性較弱。）

（2）該公司現有一個直播間銷售甲、乙兩種產品。為對產品質量進行監控，質檢人員先用簡單隨機抽樣的方法從甲、乙兩種產品中分別抽取了5件、3件產品進行初檢，再從中隨機選取3件進一步檢驗，記抽到甲產品的件數為X ，試求X 的分布列與期望。

18.（本小題17分）寒假期間小明每天堅持在“跑步3 000米”和“跳繩2 000個”中選擇一項進行鍛煉，在不下雪的時候，他跑步的概率為0.6，跳繩的概率為0.4;在下雪天，他跑步的概率為0.2，跳繩的概率為0.8。若前一天不下雪，則第二天下雪的概率為0.5;若前一天下雪，則第二天仍下雪的概率為0.4。已知寒假第一天不下雪，跑步3 000 米大約消耗能量330卡路里，跳繩2 000 個大約消耗能量220卡路里。記寒假第n 天不下雪的概率為pn（n∈N* ）。

（1）求p1，p2，p3 的值，并證明{pn -6/11} 是等比數列;

（2）求小明寒假第n 天通過運動鍛煉消耗能量的期望。

19.（本小題17 分）已知函數f （x）=ex +msin x。

（1）當m =1時，求曲線y=f（x）在點（0，f（0））處的切線方程;

（2）若函數f（x）在（0，π）上單調遞增，求正實數m 的取值范圍;

（3）求證：當m =1 時，f （x）在（-π，+∞）上存在唯一極小值點x0，且-1<f（x0）<0。

（責任編輯 徐利杰）