概率統計重點題型與解題技巧

概率統計部分內容多，在現實生活中應用廣泛，是高中數學中的重要模塊。下面就該模塊的重點題型與解題技巧進行梳理，以期對同學們的學習有所啟發。

（3）從流水線上任取5件產品，恰有2件產品的質量超過505 g的概率為C2 50.32（1-0.3）3=0.308 7。

點評：抓住問題本質，認準數學模型是解題的關鍵。本題第二問為超幾何分布，第三問為二項分布，超幾何分布的本質是把樣本分為兩類有限抽樣，二項分布的本質是獨立重復試驗。

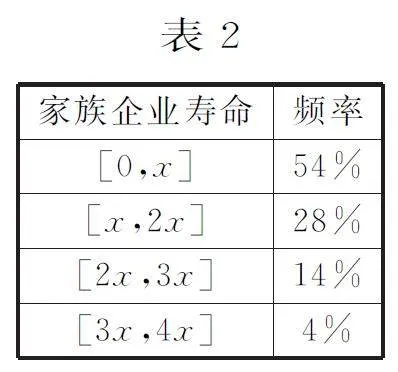
例8 “一世”又叫“一代”。東漢王充《論衡·宣漢篇》：“且孔子所謂一世，三十年也。”清代段玉裁《說文解字注》：“三十年為一世，按父子相繼曰世。”而當代中國學者測算“一代”平均為25年。另一家國家研究機構的研究報告顯示，全球家族企業的平均壽命其實只有26年，約占總量28%的家族企業只能傳到第二代，約占總量14%的家族企業只能傳到第三代，約占總量4%的家族企業可以傳到第四代甚至更久遠（為了研究方便，超過第四代的可忽略不計）。根據該研究機構的研究報告，可以估計該機構所認為的“一代”大約為（ ）。

A.23年 B.22年

C.21年 D.20年

解析：設“一代”為x 年，已知約占總量28%的家族企業只能傳到第二代，約占總量14%的家族企業只能傳到第三代，約占總量4%的家族企業可以傳到第四代，可列出頻率分布表，根據平均壽命其實只有26年，利用平均數的求法求解。

已設“一代”為x 年，企業壽命的頻率分布如表2所示。

因為全球家族企業的平均壽命其實只有26年，所以家族企業的平均壽命為：

0.54×0.5x+0.28×1.5x +0.14×2.5x+0.04×3.5x=26。

解得x≈22，選B。

點評：同學們要重視應用，學會建模。本題主要考查頻率分布表的應用以及平均數的求法，需要同學們具備一定的數學建模能力，才能把實際問題與數學知識聯系起來。

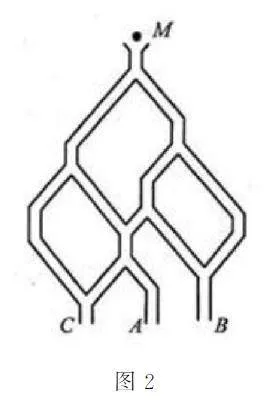
例9 如圖2，一個小球從M 處投入，通過管道自上而下落到A 或B 或C。已知小球從每個岔口落入左右兩個管道的可能性是相等的。某商家按上述投球方式進行促銷活動，若投入的小球落到A，B，C，則對應獲得一，二，三等獎。

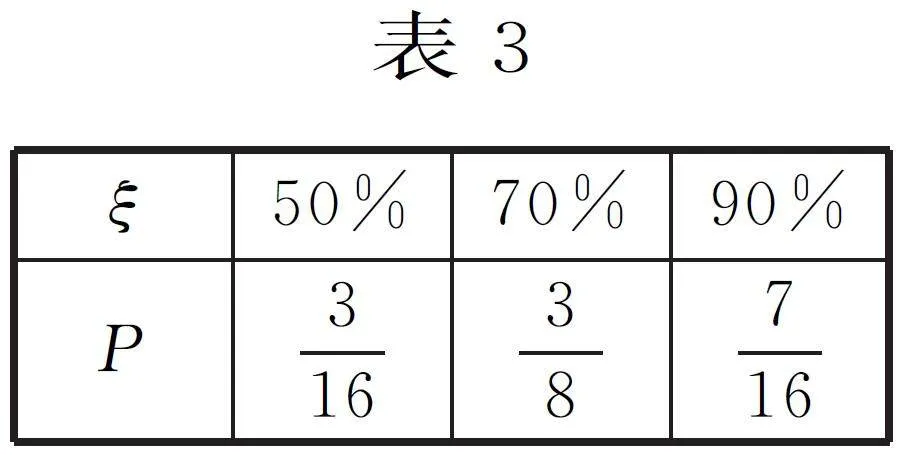
（1）已知獲得一，二，三等獎的折扣率分別為50%，70%，90%。記隨機變量ξ 為獲得k（k=1，2，3）等獎的折扣率，求隨機變量ξ 的分布列及期望E（ξ）。

（2）若有3人次（投入1球為1人次）參加促銷活動，記隨機變量η 為獲得一等獎或二等獎的人次，求P（η=2）的值。

解析：構建答題模板：

第一步，確定離散型隨機變量的所有可能取值;

第二步，弄清每個取值的意義，求出其對應概率;

第三步，列出隨機變量的分布列;第四步，求期望;

第五步，回顧解題過程，查看是否有重復或遺漏的情況，規范書寫過程。

如本題可重點查看隨機變量的所有可能取值是否正確，根據分布列性質檢查概率是否正確。

（1）由題意得ξ 的分布列如表3所示。