數學思想助力　解題思路自明

數學思想是數學知識的重要組成部分，是數學解題思路的指路明燈. 在運用一元二次方程的知識解決問題時，用數學思想助力，則解題思路自明. 下面舉例來說明.

一、整體思想

例1 關于x的一元二次方程x2 + bx + c = 0有兩個相等的實數根，則b2 - 2（1 + 2c）等于（ ）.

A. -2 B. 2

C. -4 D. 4

分析：求值式即b2 - 4c - 2，由方程有相等實根，整體求出b2 - 4c的值即可.

解：∵關于x的一元二次方程x2 + bx + c = 0有兩個相等的實數根，

∴Δ = b2 - 4c = 0，∴b2 - 2（1 + 2c） = b2 - 4c - 2 = -2，故選A.

點評：這里要分別求出b和c的值是不可能的，而將b2 - 4c視為一個整體求值，問題則迎刃而解.

二、轉化思想

例2 對于實數a，b，定義運算“?”為a?b = b2 - ab，例如：3?2 = 22 - 3 × 2 = -2，則關于x的方程（k - 3）?x = k - 1的根的情況，下列說法正確的是（ ）.

A. 有兩個不相等的實數根 B. 有兩個相等的實數根

C. 沒有實數根 D. 無法確定

分析：將方程（k - 3）?x = k - 1轉化為常規運算形式，再由根的判別式得出答案.

解：∵（k - 3）?x = k - 1，∴x2 - （k - 3）x = k - 1，∴x2 - （k - 3）x - k + 1 = 0.

∵Δ = ［-（k - 3）］2 - 4 × 1 × （-k + 1） = （k - 1）2 + 4 > 0，

∴關于x的方程（k - 3）?x = k - 1有兩個不相等的實數根，故選A.

點評：本題以新定義運算的形式考查根的判別式和實數的運算，解決這類問題的關鍵是弄清新規則，將新運算轉化為常規運算來處理. 在判定含字母系數的代數式的性質符號時，要用配方法將其轉化為“（ ）2”或“（ ）2 + 正數”或“-（ ）2”或“-（ ）2 - 正數”的形式，即可作出正確的判斷.

三、數形結合思想

例3 若一個菱形的兩條對角線長分別是關于x的一元二次方程x2 - 10x + m = 0的兩個實數根，且其面積為11，則該菱形的邊長為（ ）.

A. [3] B. 2[3] C. [14] D. 2[14]

分析：設菱形兩條對角線的長為a，b，利用根與系數的關系及對角線與菱形面積的關系得出關于a，b的等式，再求出菱形的邊長.

解：設菱形兩條對角線長分別為a，b，由題意，得[a+b=10，ab=22，]

∴菱形的邊長 = [a22+b22] = [12a2+b2] = [12（a+b）2-2ab] = [12100-44] = [14]. 故選C.

點評：本題也可先求出方程的兩實根（都含有二次根式），再用勾股定理求出菱形的邊長，但較復雜. 這里對根據勾股定理得到的表達式進行變形，與根與系數的關系聯系起來，簡潔明了.

四、模型思想

例4 若W = 5x2 - 4xy + y2 - 2y + 8x + 3（x，y為實數），則W的最小值為 .

分析：視W和y為常數，將已知式轉化為關于x的方程，由x為實數，利用根的判別式非負，借助配方即可得到答案.

解：由題意，得5x2 + （8 - 4y）x + （y2 - 2y + 3 - W） = 0.

∵x為實數，∴（8 - 4y）2 - 20（y2 - 2y + 3 - W） ≥ 0，

即5W ≥ （y + 3）2 - 10 ≥ -10，∴W ≥ -2，∴W的最小值為-2.

點評：這是求多字母代數式的最值問題，一般思路是運用配方法及偶次冪的非負性來處理，但需經過多次拆項配方才能得到結果，過程較復雜. 這里將已知式轉化為一元二次方程模型，運用根的判別式為非負數得到不等式的思路則應運而生. 由于減少了一個字母，再利用配方法及偶次冪的非負性來確定最值就容易多了.

五、分類思想

例5 已知實數s，t滿足2s2 + 3s - 1 = 0，2t2 + 3t - 1 = 0，求[1s-1t]的值.

分析：易知st ≠ 0. 從已知條件看，s與t之間有兩種情況：（1）s = t，此時易知答案為0；（2）s ≠ t，此時s，t是方程2x2 + 3x - 1 = 0的兩個不等實數根. 待求值式是s，t的倒數差，運用根與系數的關系即可得解.

解：（1）當s = t時，[1s-1t] = 0.

（2）當s ≠ t時，∵實數s，t滿足2s2 + 3s - 1 = 0，2t2 + 3t - 1 = 0，且s ≠ t，

∴s，t是方程2x2 + 3x - 1 = 0的兩個不等實數根，∴s + t = - [32]，st = - [12]，

∴（[t-s]）2 = （[t+s]）2 - [4st] [=94+2] [=174]，∴[t-s=172]或[-172].

當[t-s=172]時，[1s-1t=t-sst=-17]；

當[t-s=-172]時，[1s-1t=t-sst=17].

綜上可知，[1s-1t]的值為0或[17]或[-17].

點評：本題初看上去可求出s，t，再代入[1s-1t]求值，但十分復雜. 這里分s = t和s ≠ t兩種情況來思考求解. 當s ≠ t時，從兩個已知等式和求值式的結構出發，構造出一元二次方程，進而尋找到問題的最佳解法.

拓展訓練

1. 已知x = 1是一元二次方程x2 + ax + b = 0 的一個根，則a2 + 2ab + b2的值為 .

2. 已知a，b是方程x2 + 3x - 5 = 0的兩根，則a2 + 4a + b - 4 = .

3. 設α，β是方程（x + 1）（x - 4） = - 5的兩實數根，則[β3α+α3β] = .

4. 已知a，b是方程x2 - 3x - 5 = 0的兩根，則代數式2a3 - 6a2 + b2 + 7b + 1的值是（ ）.

A. -25 B. -24 C. 35 D. 36

5. 我們規定：對于任意實數a，b，c，d有［a，b］*［c，d］ = ac - bd，其中等式右邊是通常的乘法和減法運算，如：［3，2］*［5，1］ = 3 × 5 - 2 × 1 = 13. 已知關于x的方程［x，2x - 1］*［mx + 1，m］ = 0有兩個實數根，求m的取值范圍.

6. 如圖1，在長為100 m，寬為50 m的矩形空地上修筑四條寬度相等的小路，若余下的部分全部種上花卉，且花卉的種植面積是3600 m2，則小路的寬是（ ）.

A. 5 m B. 70 m C. 5 m或70 m D. 10 m

7. 如圖2，在△ABC中，∠ABC = 90°，BD為AC邊的中線，過點C作CE ⊥ BD于點E，過點A作BD的平行線，交CE的延長線于點F，在AF的延長線上截取FG = BD，連接BG，DF. 若AG = 13，CF = 6，則四邊形BDFG的周長為 .

8. 已知實數m，x滿足（mx1 - 2）（mx2 - 2） = 4.

（1）若m = [13]，x1 = 9，則x2 = ；

（2）若m，x1，x2為正整數，則符合條件的有序實數對（x1，x2）有 個.

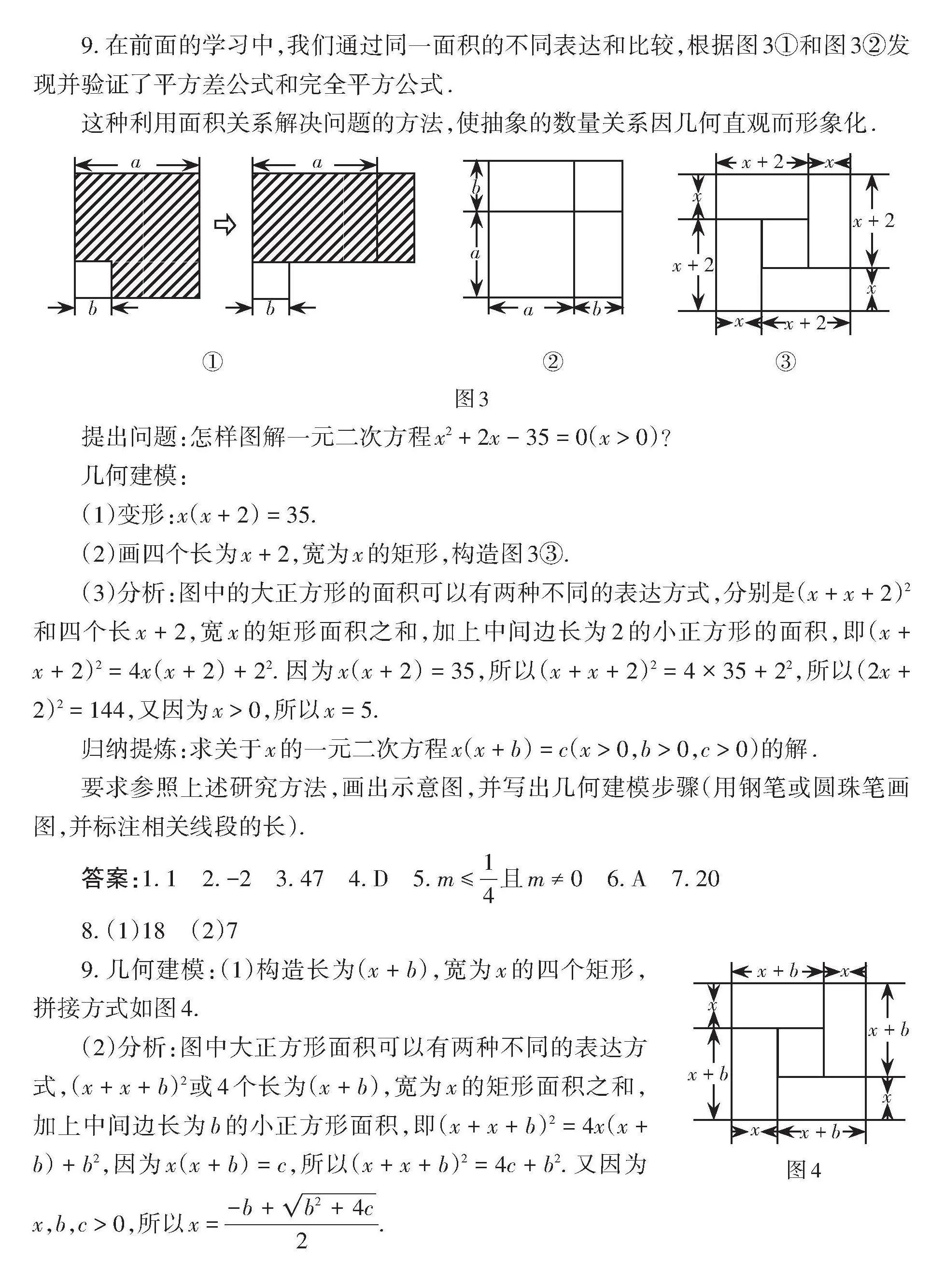
9. 在前面的學習中，我們通過同一面積的不同表達和比較，根據圖3①和圖3②發現并驗證了平方差公式和完全平方公式.

這種利用面積關系解決問題的方法，使抽象的數量關系因幾何直觀而形象化.

[b] [b] [①] [a][a] [a] [b] [a] [b][②] [x + 2][x][x][x + 2] [x][x + 2][x + 2][x][③]

圖3

提出問題：怎樣圖解一元二次方程x2 + 2x - 35 = 0（x > 0）？

幾何建模：

（1）變形：x（x + 2） = 35.

（2）畫四個長為x + 2，寬為x的矩形，構造圖3③.

（3）分析：圖中的大正方形的面積可以有兩種不同的表達方式，分別是（x + x + 2）2和四個長x + 2，寬x的矩形面積之和，加上中間邊長為2的小正方形的面積，即（x + x + 2）2 = 4x（x + 2） + 22. 因為x（x + 2） = 35，所以（x + x + 2）2 = 4 × 35 + 22，所以（2x + 2）2 = 144，又因為x > 0，所以x = 5.

歸納提煉：求關于x的一元二次方程x（x + b） = c（x > 0，b > 0，c > 0）的解.

要求參照上述研究方法，畫出示意圖，并寫出幾何建模步驟（用鋼筆或圓珠筆畫圖，并標注相關線段的長）.

答案：1. 1 2. -2 3. 47 4. D 5. m ≤ [14]且m ≠ 0 6. A 7. 20

8. （1）18 （2）7

9. 幾何建模：（1）構造長為（x + b），寬為x的四個矩形，拼接方式如圖4.

（2）分析：圖中大正方形面積可以有兩種不同的表達方式，（x + x + b）2或4個長為（x + b），寬為x的矩形面積之和，加上中間邊長為b的小正方形面積，即（x + x + b）2 = 4x（x + b） + b2，因為x（x + b） = c，所以（x + x + b）2 = 4c + b2. 又因為x，b，c > 0，所以x = [-b+b2+4c2].

（作者單位：江蘇省興化市戴澤初級中學）