具有[H∞]性能的輸入受限三級倒立擺控制器設計

摘 要：【目的】針對直線三級倒立擺控制輸入受限下的穩擺控制問題，設計了具有H∞性能的輸入受限三級倒立擺控制器。【方法】利用線性矩陣不等式（LMI）方法，將控制輸入約束問題轉化為利用線性矩陣不等式求解優化值的優化問題，經Lyapunov穩定性推導出符合條件的LMI，利用MATLAB中的LMI工具箱求解得到有效的K。進一步在控制輸入受限下引入H∞性能指標，使所設計的控制輸入受限下的算法具有H∞性能。【結果】仿真結果表明，該控制器對于控制輸入受限下的復雜高階次不穩定系統具有很好的控制效果。【結論】控制輸入信號在給定的受限范圍內實現了三級倒立擺的穩擺要求，且引入H∞性能指標后控制輸入和擺桿波動更小。

關鍵詞：直線三級倒立擺；控制輸入受限；線性矩陣不等式（LMI）；H∞性能指標

中圖分類號：UTP273 文獻標志碼：A 文章編號：1003-5168（2024）17-0004-06

DOI：10.19968/j.cnki.hnkj.1003-5168.2024.17.001

Design of Input Constrained Triple Inverted Pendulum Controller with H∞ Performance

HAN Guangxin ZHANG Baokui

（College of Information and Control Engineering， Jilin of Chemical Technology， Jilin 132022， China）

Abstract： [Purposes] To solve the stabilization control problem of triple inverted pendulum with control input constraint， an input constrained control strategy with H∞ performance is proposed.[Methods] By using linear matrix inequalities（LMI）， the control input constraint problem is transformed into an optimization problem using LMI to solve the optimization value. A suitable LMI is obtained by Lyapunov stability derivation， and an effective K is obtained by using the LMI toolbox in MATLAB. Furthermore， H∞ performance index is introduced to make the designed algorithm with control input constraint have H∞ performance. [Findings] The simulation results show that the control strategy has a good control effect on the complex high-order unstable system with control input constraint. [Conclusions] The control input signal can achieve the stability requirement of the triple inverted pendulum within the given limited range， and the fluctuation of the control input and pendulum rod is less after the introduction of H∞ performance index.

Keywords： linear triple inverted pendulum; control input constraint; linear matrix inequality（LMI）; H∞ performance

0 引言

控制輸入受限問題［1］在實際的控制系統中是廣泛存在的。由于其自身的物理特性而引起的執行機構飽和約束，例如，在汽車主動懸架控制系統［2］中，力發生器只能產生有限的作用力；在化工反應釜生產過程控制中，填料速率［3］不可能無限地快，必然要有個限度。因此，對于控制輸入受限的研究［4-6］具有十分重要的現實意義。如果只考慮系統性能而忽略控制輸入約束，那么在實際應用時極有可能會因執行機構限制而造成整個控制系統發散，進而導致整個控制系統失控。即使系統不發散，長時間高強度的振蕩也會造成控制系統結構損壞，從而導致故障。在不超出規定的約束范圍內，完成倒立擺的穩擺控制目標，對于諸多的實際控制系統來說，具有極為值得借鑒的現實意義。

對于控制輸入受限的控制器設計方法分為兩大類。一類為補償器設計法［7］：即通過定義輔助系統，采用輸入飽和誤差動態放大的方法，可以實現一種基于控制輸入抗飽和控制；另一類為直接法：即在設計控制器之時就考慮控制輸入受限，使控制輸入在給定的受限范圍內完成穩擺控制目標。本研究采用直接法設計，將約束條件轉化為線性矩陣不等式［8-9］的條件，求解出有效的控制器增益，使控制輸入在給定的有限范圍內實現對三級倒立擺的控制。

1 數學模型

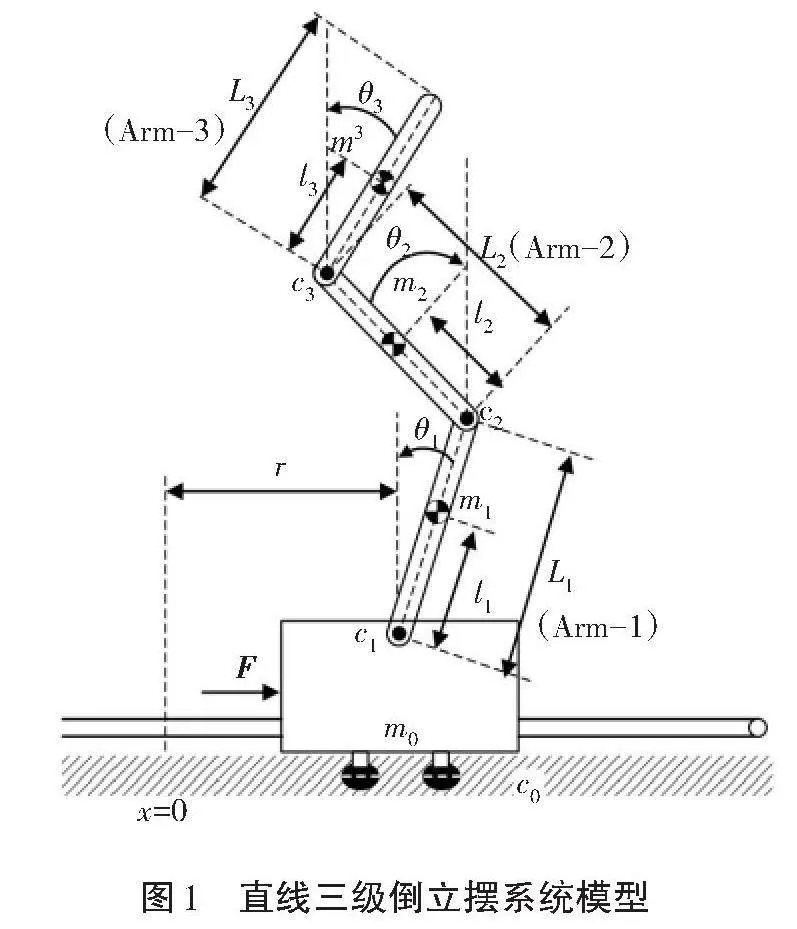
直線三級倒立擺系統簡化模型如圖1所示。在系統建模時定義擺桿正旋轉方向為逆時針，小車位移的正方向為向右運動，以擺桿垂直位置為0。下擺桿離垂直位置的偏角為[θ1（t）]，中擺桿離垂直位置的偏角為[θ2（t）]，上擺桿離垂直位置的偏角為[θ3（t）]。

在對直線三級倒立擺系統應用拉格朗日力學［10］的方法進行建模時，分別列出小車、下擺、中擺、上擺、質量塊1和質量塊2這6個部分的動能和勢能。之后構建拉格朗日算子，列寫出拉格朗日方程，對所得到的微分方程組化簡后，即可得到三級倒立擺系統的非線性數學模型。

利用拉格朗日方程推導運動學方程，對于直線三級倒立擺系統，系統的總動能見式（1）。

[T=T0+T1+T2+T3+T4+T5] （1）

系統的總勢能見式（2）。

[V=V0+V1+V2+V3+V4+V5] （2）

拉格朗日方程見式（3）。

[L=T-V] （3）

式中：[L]為系統的總動能與總勢能之差。

在倒立擺系統進行建模時，在理想條件下（忽略摩擦和干擾），小車和擺桿相對于伺服電機而言，電壓的拉格朗日方程的一般形式表示見式（4）。

[ddt?L?qi-?L?qi=Qi] （4）

式中：[qi]為廣義坐標。

對于直線三級倒立擺系統，則存在的關系見式（5）。

[qi（t）T=x（t）θ1（t）θ2（t）θ3（t）] （5）

系統在[θ1（t）]、[θ2（t）]、[θ3（t）]方向上不受外力，在小車水平方向上受外力[F]，且[F]為系統的控入輸入量[u]，則等式（6）成立。

[?2L?t?x-?L?x=F=u?2L?t?θ1-?L?θ1=0?2L?t?θ2-?L?θ2=0?2L?t?θ3-?L?θ3=0] （6）

對于直線三級倒立擺系統而言，其工作點是倒立擺系統保持在平衡狀態下各個變量的值，在倒立擺處于平衡狀態時，系統在平衡點處線性化，則有[sinθ≈0，cosθ≈1]。

假定系統保持豎直向上的平衡狀態時，所有狀態都取零，見式（7）。

[X=xθ1θ2θ3xθ1θ2θ3T=[00000000]T] （7）

將式（6）得到的微分方程組，在平衡點位置附近用Taylor Series展開并代入此刻狀態變量的值，運用Mathematica科學計算軟件進行計算，且取[x]作為輸入，令控制輸入量等于加速度，即[u=x]。系統的線性狀態方程見式（8）。

[X=AX+BuY=CX] （8）

將倒立擺機械系統的結構參數值代入，即可得到三級倒立擺的線性數學模型，具體見文獻［11］。

為了得到存在外部擾動不確定性因素的三級倒立擺數學模型，將小車與三級擺桿作為一個整體系統，外界擾動作為系統的輸入，可以得出的結果見式（9）。

[x=u-wM] （9）

式中：[M]表示小車、三級擺桿和質量塊的總質量；[w]表示系統的建模誤差及外界輸入擾動。

因此，可得到三級擺不確定性數學模型的狀態空間方程見式（10）。

[X=AX+B1w+B2uY=CX] （10）

式中：[A=]

[00001000000001000000001000000001000000000159.504-38.435 60.784 64600000-127.957.9951-17.189000002.570 86-16.924 539.348 50000；]

[B1=0 0 0 0 -1 -6.649 04 0.158 31-0.003 182 11T]；[B2=0 0 0 0 1 6.649 04 -0.158 31 0.003 182 11T]；

[C=1000000001000000001000000001000000001000000001000000001000000001] 。

2 控制器設計與分析

2.1 具有H∞性能指標的輸入受限下LMI控制器

根據三級倒立擺系統模型式（10），控制器設計見式（11）。

[u=KX] （11）

式中：[K=k1k2k3k4k5k6k7k8]。

控制目標為[t→∞]時，在控制輸入滿足[|u|?umax]條件下，使得[X→0]且[||Gzω（s）||∞<γ]，把控制目標轉化為LMI設計，推導得到具有H∞性能指標的輸入受限下三級倒立擺控制結論見式（12）。

[AN+BF+NAT+FTBTBBT-γ2<0N>0， N=NTk0NFTF1≥0wX0TX0N≥0] （12）

通過式（12）構造的4個LMI，可求得具有H∞指標的控制輸入受限下［12］有效的[K]，其中：[P]是李雅普諾函數設計的正定矩陣，[F=KP-1]，[N=P-1]，[X0]是倒立擺系統初始狀態，其余為待選參數。

2.2 具有H∞性能指標的LMI控制器設計分析

根據模型式（10）相當于在狀態方程中加入擾動[d]，模型可表示為式（13）。

[X=AX+Bu+dY=CX] （13）

設計的Lyapunov函數見式（14）。

[V=XTPX] （14）

其中[P>0]為8×8階正定矩陣，通過P的設計可有效調節X的收斂效果。

[V=XTPX+XTPX=（AX+Bu+Bd）TPX+XTP（AX+Bu+Bd）=（AX+BKX+Bd）TPX+XTP（AX+BKX+Bd）=XT（A+BK）TPX+XTP（A+BK）X+（Bd）TPX+XTP（Bd）=XTQT1X+XTQ1X+（BTPX+XTPB）d=XTQX+（BTPX+XTPB）d]

（15）

式中：[Q1=P（A+BK）]，[Q=QT1+Q1]。

[令η=XTdT，則η=Xd， ηT=XTd]

從而得到式（16）和式（17）。

[XTQX=XTdQ000Xd]

[=ηTQ000η] （16）

[BTPX+XTPBd=dBTPXTPBXd=XTd0PBBTP0Xd=ηT0PBBTP0η] （17）

即：

[V=XTQX+ηT0PBBTP0η=ηTQPBBTP0η] （18）

輸出為 [Z=CX]， 則H∞性能指標取式（19）。

[0tZTZdt<0tγ2d2（t）dt+V（0）]（[γ>0]） （19）

由于式（20）和式（21），則得出式（22）。

[ZTZ-γ2d2=XTCTCX-γ2d2] （20）

[ηTCTC00-γ2η=XTdCTC00-γ2Xd]

[=XTCTC-γ2d2Xd=XTCTCX-γ2d2] （21）

[ZTZ-γ2d2=ηTCTC00-γ2η] （22）

從而[V+ZTZ-γ2d2=ηTQ+CTCPB（PB）T-γ2η] （23）

取[θ=Q+CTCPB（PB）T-γ2<0] （24）

則[V+ZTZ-γ2d2≤0] （25）

對上式積分，可得式（26）。

[V+0tZTZdt≤0tγ2d2dt+V（0）] （26）

假設[d]為遞減的擾動信號，即積分有界擾動，取：

[0∞d2 dt≤γ-2vmax] （27）

由于[0tZTZdt≥0，則：]

[V（t/aLo1CNMnnqxDbHZQ/L0YiBjOVQrTAe/759T14Uw3oU=）≤w] （28）

其中[vmax +V（0）≤w]。

由[V（t）≤w]可得式（29）。

[Pmin ‖X‖2≤XTPX≤w] （29）

則收斂結果為式（30）。

[‖X‖2≤vmax+V（0）Pmin] （30）

將式（24）展開即可得到滿足H∞性能指標的條件：

[PA+PBK+ATP+KTBTPPB（PB）T-γ2<0] （31）

左右兩邊同時乘[P-1001]

[AP-1+BKP-1+P-1AT+P-1KTBTBBT-γ2<0] （32）

令[F=KP-1，][ N=P-1]。由式（32）可化為LMI設計形式，得到第一個LMI，見式（33）。

[AN+BF+NAT+FTBTBBT-γ2<0] （33）

根據[P]的定義可設計第二個LMI，見式（34）。

[N>0， N=NT] （34）

2.3 控制輸入受限下LMI控制器設計分析

由于[V（0）=X0TPX0]，如果存在正定矩陣P和[w>0，]使得[X0TPX0≤w]成立，則可保證[V（0）≤w]，從而[V（t）≤w]。

取[KTK?w-1u2maxP]，由[u=KX]可得式（36）。

[u2=（KX）TKX=XTKTKX≤XTw-1u2maxPX=w-1u2maxV≤u2max] （35）

則 [|u|?umax] （36）

通過上述理論分析，可以構造線性矩陣不等式見式（37）。

[KTK-w-1u2maxP≤0] （37）

由于不等式（37）中含有非線性項，必須轉化為線性矩陣不等式才能求解。故取[k0=w-1u2max]，則有式（38）。

[KTK≤k0P] （38）

根據Schur補定理［13］，假設[C]為正定矩陣，則[A-BC-1BT≥0]等價于[ABBTC≥0]，則有式（39）。

[k0PKTK1≥0] （39）

式（39）左右兩邊同時乘[P-1001]，則有式（40）。

[k0P-1P-1KTKP-11≥0] （40）

[取F=KP-1， N=P-1]根據式（40）可得到第三個LMI，見式（41）。

[k0NFTF1≥0] （41）

要滿足[X0TPX0≤w]，根據Schur補定理，可以將其設計為第四個LMI，見式（42）。

[wX0TX0N≥0] （42）

通過式（33）、式（34）、式（41）、式（42）構造的4個LMI，可求得具有H∞指標的控制輸入受限下有效的[K]。

3 仿真結果

采用Matlab中的LMI工具箱—YALMIP求解倒立擺初始值為小車位置-0.5 m，上擺桿、中擺桿、下擺桿分別為-0.2 rad、0.1 rad、0.1 rad。控制器參數為[w=1.0、α=2.0、γ=0.5][umax=20]。即可得到H∞指標的控制輸入受限控制器反饋增益：[K =0.1118 ]

[-106.8847 90.4163 -132.2230 0.3735 -4.8538 ][8.1204 -19.8516]。

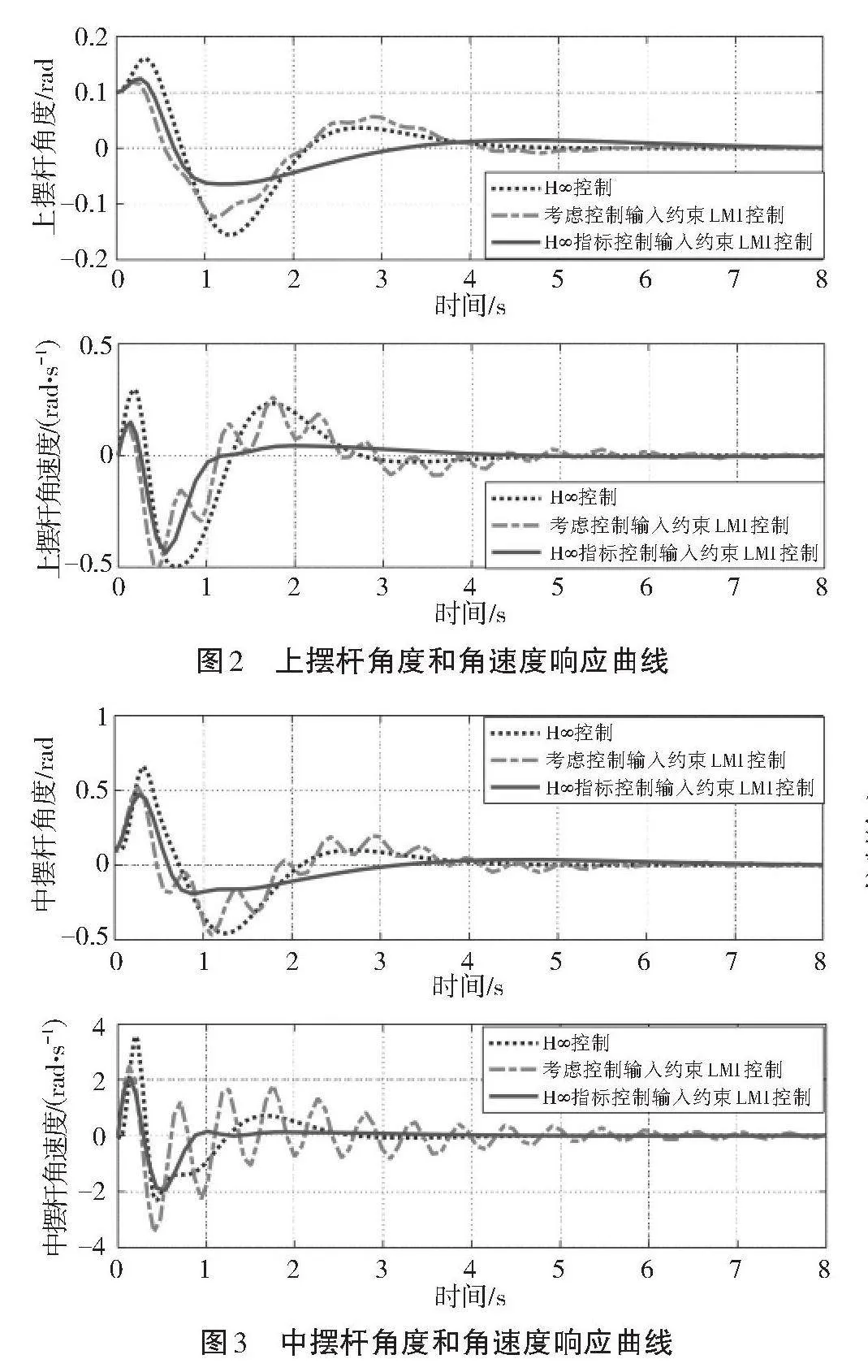
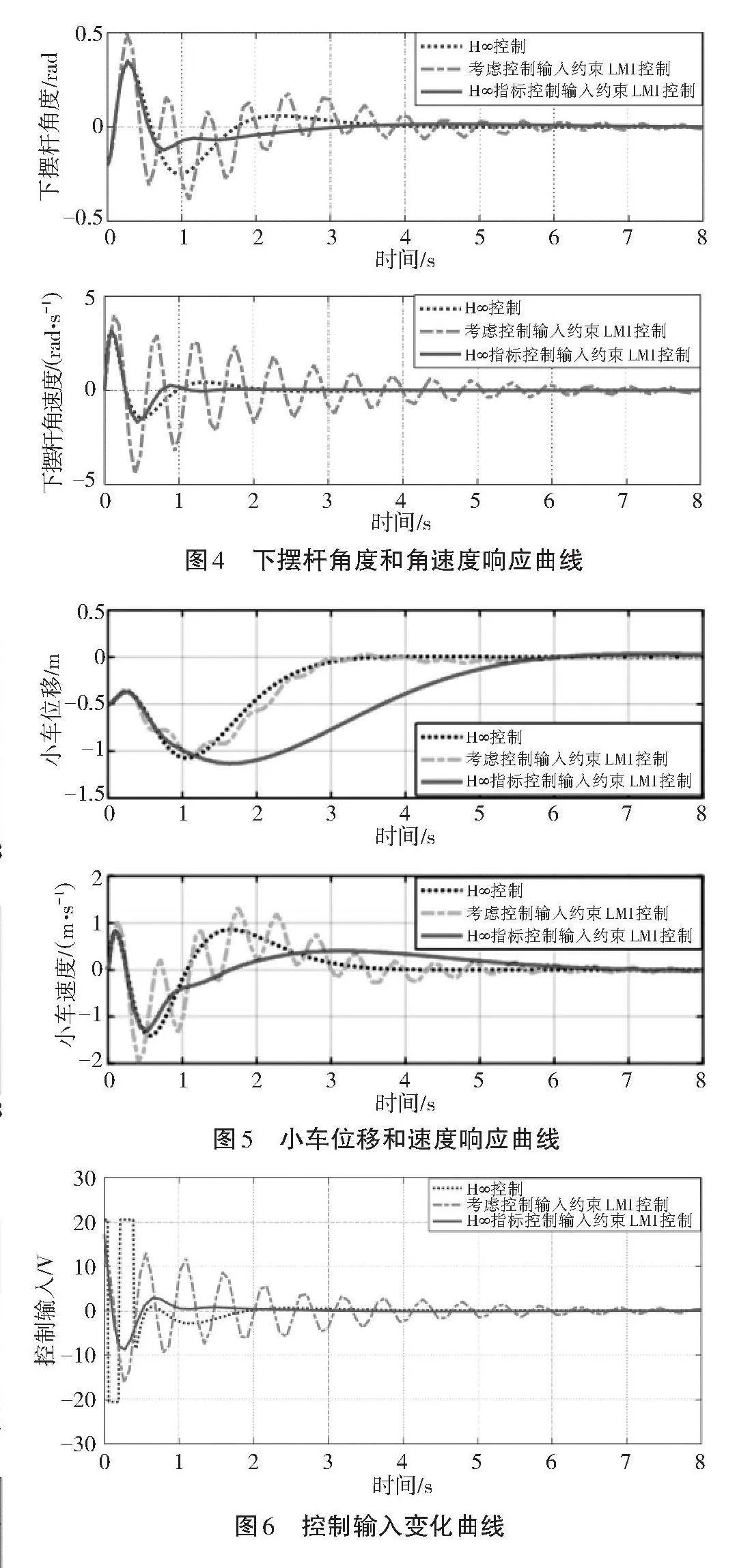
對比算法選用H∞控制器［14-15］實現三級倒立擺穩擺控制目標可以看出控制輸入不滿足限制的要求，采用直接法線性矩陣不等式技術可以直接考慮控制輸入，使控制輸入在給定的受限范圍內對直線三級倒立擺達到穩擺控制的要求。為了進一步對比出效果，H∞控制器的控制輸入利用限幅模塊對其進行壓縮，壓縮到20.5 v系統已發生變形，再壓縮系統將發散變得不穩定，無法達到期望的控制輸入20 v條件下穩擺的控制目標。控制輸入約束下LMI控制器則可以使控制輸入在期望的受限范圍內完成控制目標，加入H∞指標控制輸入約束LMI控制器也可以在控制輸入被限制的范圍內完成穩擺的控制目標且擺桿具有更小的波動，仿真實驗過程如圖2至圖6所示。

4 結論

針對直線三級倒立擺高階次欠驅動系統控制輸入受限下的控制問題，本研究基于線性矩陣不等式采用直接法解決控制輸入受限問題，推導出考慮控制輸入受限時的LMI，利用LMI工具箱求解出有效的K，使三級倒立擺在保證控制輸入在期望范圍內完成穩擺控制目標，再進一步引入H∞性能指標使擺桿和控制輸入在波動上更為平穩，有更為優越的控制性能。經仿真實驗驗證所提控制算法的有效性，控制輸入受限下和引入H∞指標控制輸入約束LMI控制器均達到了控制輸入信號在給定的受限范圍內對直線三級倒立擺穩擺的控制要求，也進一步說明了線性矩陣不等式對于解決高階次復雜非線性系統控制方面的有效性。

參考文獻：

［1］ZHAO W，LIU Y，YAO X Q.Pde-based boundary adaptive consensus control ofmultiagent systems with input constraints［J］.IEEE Transactions on Neural Networks and Learning Systems，2023.

［2］賈俊茹，鄭黎明，張鎮.汽車非線性主動懸架系統的自適應事件觸發控制［J］.汽車安全與節能學報，2023，14（4）：439-447.

［3］袁建華，陳慶，劉力溥.基于催化劑與變進料比控制的化工生產反應速率及轉化率的研究［J］.三峽大學學報（自然科學版），2018，40（4）：74-78.

［4］LI B，YONG K，CHEN M， et al. Flexible performance‐based adaptive fault‐tolerant attitude tracking control for input‐constrained satellite［J］.International Journal of Adaptive Control and Signal Processing，2023，37（12）：3193-3211.

［5］賀戰勝，邱宏凌，沈俊.輸入受限下無人直升機自適應固定時間滑模控制［J/OL］.控制與決策：1-9［2024-05-17］.https：//doi.org/10.13195/j.kzyjc.2023.1354.

［6］韓光信，付偉，劉冬.控制輸入受限的四水箱系統分布式預測PI控制［J］.吉林化工學院學報，2019，36（9）：51-53.

［7］路瑩昕，韓光信.輸入受限的倒立擺系統變結構PID控制研究［J］.河南科技，2019（16）：37-38.

［8］呂申，武俊峰.基于LMI優化的魯棒控制器設計［J］.工業儀表與自動化裝置，2017（3）：123-125，128.

［9］甄玉婕，王天成.基于LMI的不確定隨機時滯系統輸出反饋保性能控制［J］.魯東大學學報（自然科學版），2023，39（2）：146-152.

［10］BAEK J， LEE C， LEE Y S， et al. Reinforcement learning to achieve real-time control of triple inverted pendulum［J］.Engineering Applications of Artificial Intelligence， 2024， 128： 107518.

［11］齊心舒.智能控制算法設計及倒立擺實現［D］.呼和浩特：內蒙古大學，2018.

［12］陳虹，韓光信，劉志遠.基于LMI的約束系統H∞控制及其滾動優化實現［J］.控制理論與應用，2005（2）：189-195.

［13］曾誠，馮林安.Schur補和矩陣不等式［J］.貴陽學院學報（自然科學版），2011，6（2）：12-14.

［14］夏炎，謝瑋.基于魯棒H∞理論的三級倒立擺控制系統研究［J］.計算技術與自動化，2017，36（1）：17-22.

［15］吳文波，李小華，程萬勝.基于LMI三級倒立擺系統的H∞魯棒控制［J］.遼寧科技大學學報，2010，33（3）：253-257.

收稿日期：2024-05-17

作者簡介：韓光信（1971—），男，博士，教授，研究方向：欠驅動機器人運動控制、非線性控制、帶約束控制、魯棒控制。

通信作者：張保葵（1999—），男，碩士生，研究方向：倒立擺系統控制算法研究。