三視圖補線技巧——線面法、數點法

［摘 要］三視圖補線是通用技術高考中的一種經典題型，因其對學生綜合素養的高要求而成為教學的重難點。文章根據三視圖形成過程（正投影）的特征提出兩種補線技巧：線面法和數點法。線面法，即將體的投影視為多個面的投影之和，根據某面正投影的真實性、相似性、積聚性特征補線并驗證；數點法，即在線面法的基礎上，將某個面的投影視為多個點的投影之和，根據某點正投影的三等關系特征以及數點的順序補線。將體的投影逐步分解為面、線、點的投影便可大大降低思維難度，提高解題速度與正確率。

［關鍵詞］三視圖；正投影；線面法；數點法；相似性

［中圖分類號］ G633.98 ［文獻標識碼］ A ［文章編號］ 1674-6058（2024）27-0018-03

《普通高中通用技術課程標準（2017年版2020年修訂）》對“圖樣表達”核心素養的說明為：學生能識讀簡單的機械加工圖及控制框圖等常見技術圖樣；能分析技術對象的圖樣特征，會用手工和二維、三維設計軟件繪制簡單的技術圖樣等；能通過圖樣表達設計構想，用技術語言實現有形與無形、抽象與具體的思維轉換。

三視圖作為培養學生圖樣表達能力的一個載體，以補線的形式出現，旨在讓學生根據已有的線條分析物體的結構特征。通過省去軸測圖的方法，讓學生想象該結構的加工或繪制過程，以更好地檢測學生抽象思維與具體思維的轉換能力。三視圖補線因空間想象難度大，對學生綜合素養要求高，而成為通用技術考試中的重難點。如何在短時間內準確地完成補線，是提高分數、拉開差距的關鍵。為此，教師總結出了許多解題技巧，如軸測圖繪制法、拐點法等。筆者所在的教研組通過探究三視圖形成過程（正投影）的特征，嘗試提出線面法、數點法這兩種補線技巧，希望能為相關的教育教學提供參考。

一、思路簡介

將某個結構體的投影分解為構成該結構的面的投影，甚至分解到點，逐步降低空間維度，從而降低思維難度，是本文中兩種三視圖解題技巧的關鍵思路。因此，從分析面與點的投影特性出發，可以幫助我們更好地理解并掌握解題技巧。

物體在光線的照射下，會在地面或墻面上投下影子。正投影即當投射線與投影平面垂直時，在投影平面上求取物體的投影方法。本節將簡單闡述在正投影下面和點的投影特征，以及依據這些特征而提出的線面法和數點法。

（一）面的正投影特征及線面法

1.面的正投影特征

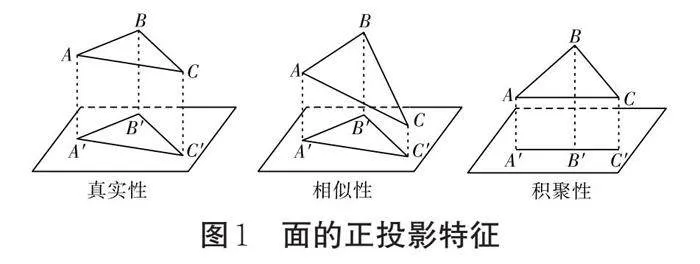
由正投影易得：當面ABC與某一投影面平行時，所得的投影即為其本身；當面ABC與某一投影面處于傾斜狀態（成一定的角度）時，所得的投影則是一個與其本身形狀一致但面積有所縮小的圖形；當面ABC與某一投影面垂直時，所得的投影將積聚為一條線段。我們可以將這三種不同情況下的投影特征分別稱為真實性、相似性、積聚性，如圖1所示。

2.線面法

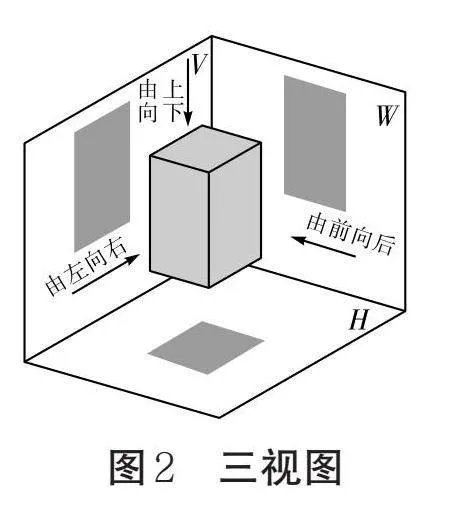
對于一個復雜的物體，為了更加準確地描述其結構形狀，我們一般會采用多面正投影法——利用三個互相垂直相交的投影面（正面投影面V、水平投影面H和側面投影面W）建立一個三投影面體系，再采用正投影法將物體同時向三個投影面投影，得到三個投影圖，分別稱為主視圖（由前向后，在正面投影面上形成的投影圖）、俯視圖（由上向下，在水平投影面上形成的投影圖）和左視圖（由左向右，在側面投影面上形成的投影圖）。主視圖、俯視圖、左視圖統稱為三視圖，如圖2所示。

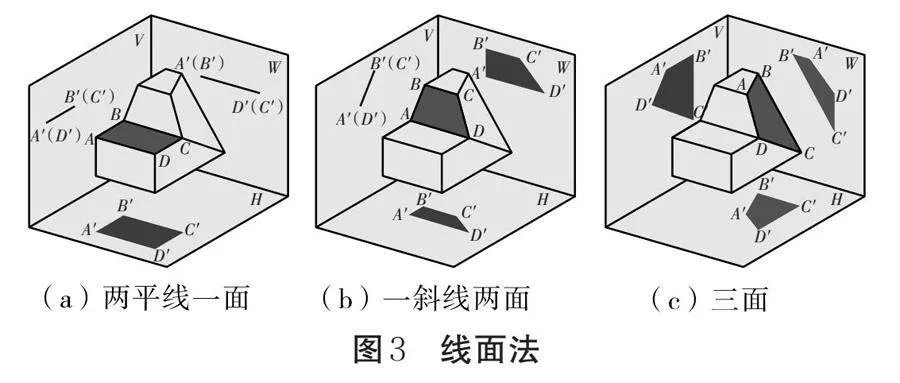
若某個面（如面ABCD）的位置非常特殊，與三個投影面中的兩個投影面V、W都垂直，與另一個投影面H平行。根據面的正投影特征可知，該面在投影面V和投影面W上的投影均為一條水平的線段——積聚性；在投影面H上的投影與其本身的形狀大小均一致——真實性。它的三個投影圖可簡稱為“兩平線一面”，如圖3（a）所示。

若某個面的位置較為特殊，僅與一個投影面V垂直，與另兩個投影面W、H均呈傾斜關系。根據面的正投影特征可知，該面在投影面V上的投影為一條傾斜的線段——積聚性；在投影面W、H上的投影均為一個與其本身的形狀一致但面積有所縮小的圖形——相似性。它的三個投影圖可簡稱為“一斜線兩面”，如圖3（b）所示。

若某個面的位置關系一般，與三個投影面V、W、H均呈傾斜關系。根據面的正投影特征可知，該面在投影面V、W、H上的投影均為一個與其本身形狀一致但面積有所縮小的圖形——相似性。它的三個投影圖可簡稱為“三面”，如圖3（c）所示。

線面法口訣為“兩平線一面”“一斜線兩面”“三面”。我們可以從三視圖已給出的輪廓線的“平”“斜”“虛”“實”來判斷被投影面與投影面的位置關系，再根據口訣補全缺失的圖線并利用投影的相似性判斷所補線條的正確性。

（二）點的正投影特征及數點法

1.點的正投影特征

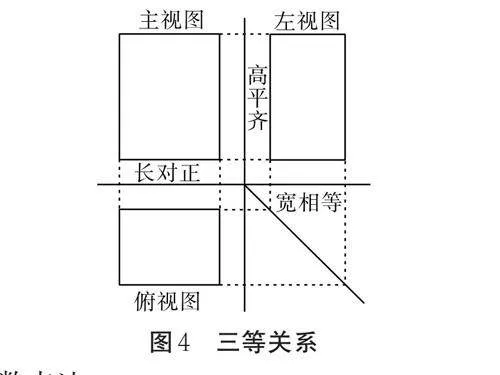
在三視圖中，主視圖反映物體的長和高，俯視圖反映物體的長和寬，左視圖反映物體的高和寬。因此三視圖存在以下投影規律：主、俯視圖長對正；主、左視圖高平齊；俯、左視圖寬相等——三等關系。

2.數點法

若某個面的形狀復雜或位置關系一般（與三個投影面均呈傾斜關系），其在某視圖中投影圖線缺失時，需要補線。由于題中未提供軸測圖，單憑空間想象難度較大且易出錯。此時可再次進行降維處理——將面的投影看作點的投影的連線。

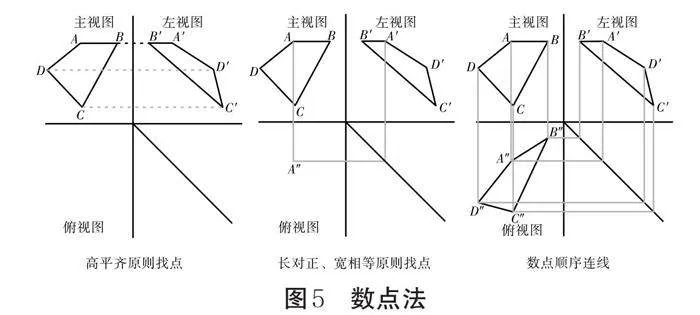
如圖5所示，已知某面與三個投影面均呈傾斜關系，其在主視圖、左視圖中的投影是完整的，現在需要在俯視圖中畫出該面的投影。

我們可以在主視圖中將該面上的點按照一定的順序標號，再根據高平齊原則標出這些點在左視圖上的位置，接著根據長對正、寬相等原則找出各點在俯視圖的投影并按照順序連線，最后還可用所得投影的相似性檢驗所補線段的正誤。

二、補線技巧及其應用

當我們面對一個結構體時，首先可用組合或切割的思路粗略分析其大致的加工過程；再根據加工的過程，將體的投影看成是由加工所得的面的投影的總和；最后借助線面法、數點法等技巧進行解題。

（一）例題

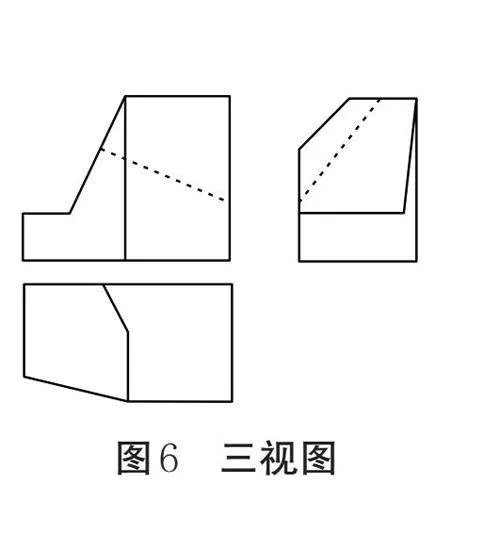
請補全三視圖（如圖6）中所缺的3條圖線。

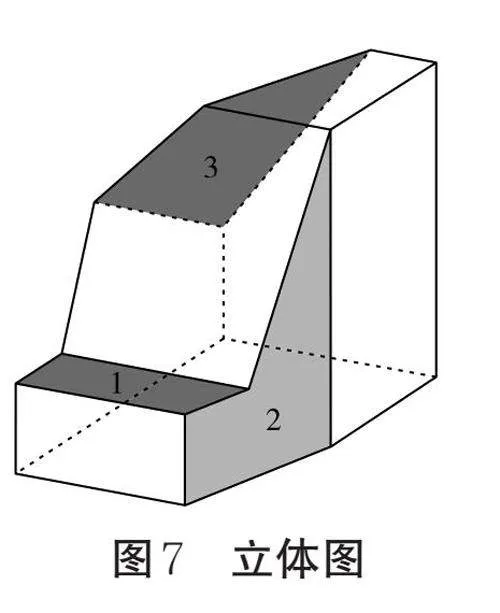
該結構可看作由一個長方體進行三步加工而得。第一步，由主視圖可得，該長方體的左上角切去了一塊截面為梯形的四棱柱；第二步，由俯視圖可得，該長方體的左前方切去了一塊截面為三角形的三棱柱；第三步，結合三視圖可得，該長方體的右后方切去了一塊復雜結構，切割后形成了一個與三投影面均不垂直的面。（立體圖僅為幫助理解，實際解題時無須繪制。圖7中的1、2、3分別對應三步加工形成的部分加工面）

（二）線面法及其應用

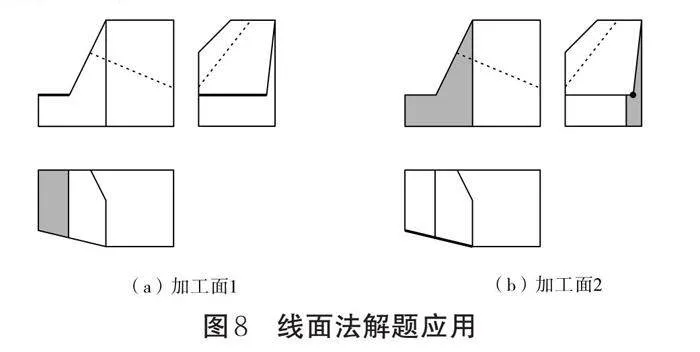
觀察例題，我們發現加工面1與正面投影面和側面投影面均垂直，與水平投影面平行，因此它的投影屬于“兩平線一面”的類型。結合已有三視圖很容易發現主視圖左側加粗的水平線段和左視圖對應等高位置處加粗的水平線段為該加工面的“兩平線”；可推斷在俯視圖的對應處缺少“一面”，如此便可快速鎖定位置并根據三等關系補線，如圖8（a）所示。

再觀察俯視方向切去三棱柱后形成的加工面2，該面與水平投影面垂直，與正面投影面和側面投影面均傾斜，其對應的投影應屬于“一斜線兩面”的類型。俯視圖左下角的一條加粗傾斜線段即為“一斜線”，主視圖中與該斜線長對正之處已有一五邊形，根據高平齊和寬相等原則可在左視圖對應位置處補出另一個形狀相似的五邊形，這兩個五邊形即為“兩面”，如圖8（b）所示。

此題的易錯點在于不少學生會從左視圖的拐點（黑點標注處）作垂線，如此所得的圖形為四邊形。在掌握了線面法后，學生可由相似性規律（兩投影形狀一致，應均呈現為五邊形）自行檢查，以判斷所補線段的正誤。

（三）數點法及其應用

當某個面與任一投影面均不垂直時，三個投影面上會呈現出三個相似的面，即“三面”。這類投影涉及的維度更多，立體感更強，需要降維處理，此時可使用數點法。

此題的難點為右后方切去一個復雜結構后所形成的加工面3，該加工面與三個投影面均呈傾斜關系，其對應的投影應屬于“三面”的類型。觀察可得，該結構在主視圖與左視圖上的投影是完整的，且均為四邊形，可推斷在俯視圖對應處需補出一個形狀相似的四邊形。

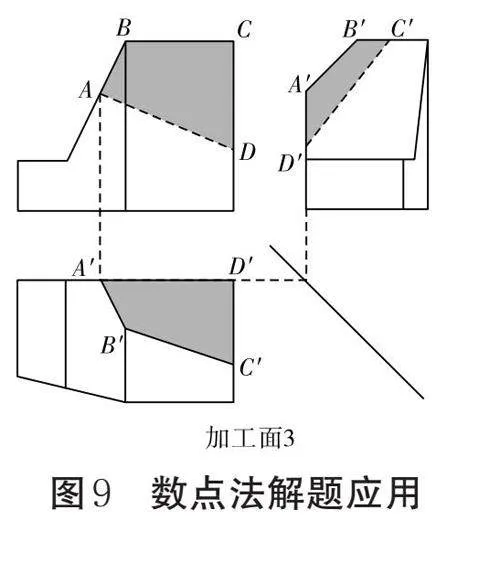
如圖9所示，應用數點法補線：先按照順時針的順序將主視圖四邊形的各個點標為ABCD，再根據高平齊原則在左視圖上標出各點的對應投影[A'B'C'D']（由于BC等高，光憑高度關系難以直接確定具體的位置，此時可根據連接的順序判斷出與[A']相連的是[B']）。確定了四個點在主視圖、左視圖上的位置后，使用三等原則畫出各點在俯視圖上的對應位置，再將所得的點按照順序連線并根據相似性規律判斷正誤。（圖9中僅展示了點A投影的尋找過程）

三、現有方法優缺點總結

三視圖補線是通用技術高考中的常考題型，以往補線時常用的方法主要有：軸測圖繪制法、拐點法。軸測圖繪制法：根據已有的三視圖，用組合法或切割法逐步繪制出軸測圖。該方法能夠很好地展現結構加工成形的整個過程，并引導學生立足整體去解題。所繪的軸測圖雖然可以降低對空間想象能力的要求，但該方法所花費的時間較長，且對學生繪制圖樣的能力有較高的要求。拐點法：常用的口訣是“有折必有線”。該方法雖然可以幫助我們快速鎖定因面面相交而產生的交線，但只能大致判斷交線所在的位置，無法確定線段的起始點。當物體結構復雜時，有轉折的地方也可能只呈現為一個折點而非交線。在這種情況下若依舊使用拐點法，會將解題者的思路引入歧途。

本文介紹的線面法和數點法立足整體、著眼局部，是根據正投影的原理，依照“體—面—線—點”的投影層層降維的分析方法，在復雜結構中有較好的應用。但這兩種方法對學生的基礎有一定的要求，初學者在理解和應用上會有些困難。

三視圖在通用技術紙筆測試中有著舉足輕重的地位，“圖樣表達”核心素養是高校理工科類專業需具備的重要素養，其包含的抽象思維與具象思維相互轉換的能力在生活的各個方面都有或大或小的作用。技巧可以幫助我們高效解題，但想真正實現質的飛躍仍需將精力放在空間想象能力的提升上。以培養能力為主、善用技巧為輔，能夠根據不同題型的特點靈活選擇適合的補線技巧是三視圖提分的關鍵。

［ 參 考 文 獻 ］

［1］ 中華人民共和國教育部.普通高中通用技術課程標準：2017年版2020年修訂［M］.北京：人民教育出版社，2020.

［2］ 梁靈輝，陳湛.指向深度學習的三視圖變式設計［J］.中學教學參考，2021（30）：42-44.

［3］ 朱仕成.基于平面立體的三視圖繪制正等軸測圖教學探析［J］.中學理科園地，2021（1）：60-61.

［4］ 沈杰.三視圖補線線索探究［J］.新課程（下），2019（11）：222-223.

［5］ 顧建軍.高中通用技術教學參考書 必修 技術與設計１［M］.南京：江蘇鳳凰教育出版社，2009.

（責任編輯 羅 艷）