緊扣“聯系”，提高學習效率

圓既是日常生活中常見的圖形之一，又是平面幾何中的基本圖形。之前，我們學習了直線、射線、線段、角、平行線，以及三角形、四邊形等幾何圖形，這些可以統稱為直線形。而圓是一個曲線形，從直線形到曲線形，在認識上是一個飛躍。

我們要學習本章的哪些內容呢？我們該如何既輕松又高效地學習這些內容呢？這兩個問題都可以通過“聯系”得到解決。

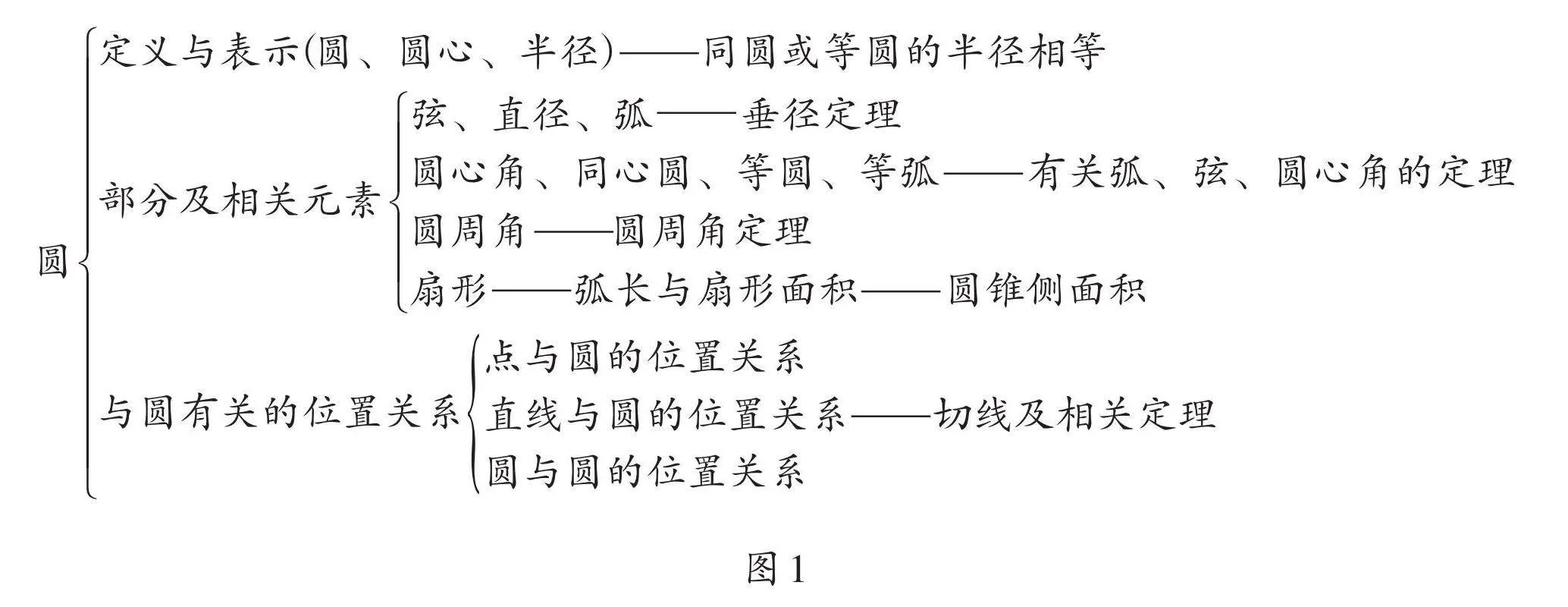
首先，我們可以將研究圓與直線的基本思路聯系起來。我們知道，研究直線的基本思路是：定義與表示→研究直線的部分及相關元素（射線與線段）→研究兩條直線的位置關系。其實，這也是研究一個平面幾何圖形的基本思路。按此思路，研究圓的基本思路是：定義與表示→研究圓的部分及相關元素（半徑、直徑、弦，弧，圓心角、圓周角，扇形）→研究與圓有關的位置關系（點與圓的位置關系，直線與圓的位置關系，圓與圓的位置關系）。同時，圓具有特殊的對稱性——軸對稱性和旋轉不變性：通過圓的軸對稱性，探索“垂徑定理”，建立圓中直徑、弧、弦之間的關系；通過圓的旋轉不變性，探索“有關弧、弦、圓心角的定理”，建立弧、弦、圓心角之間的關系（圓的思維導圖見圖1）。由于正多邊形是一種特殊的多邊形，它有一些類似于圓的性質，所以本章還會研究正多邊形的概念及正多邊形和圓的關系。

其次，我們要將圓中不同內容之間的研究方法聯系起來。比如，圓心角與圓周角是圓中很重要的兩個概念，我們可以從構成角的兩個要素（頂點、邊）出發，類比圓心角學習圓周角，并且在特定條件下，兩者有確定的數量關系；又如，點與圓的位置關系、直線與圓的位置關系、圓與圓的位置關系都體現幾何特征與代數特征的一致性以及位置關系與數量關系之間的邏輯性，而且直線與圓的位置關系也是通過過圓心作直線的垂線段轉化為點（垂足）與圓的位置關系；再如，在證明圓周角定理時，通過分類思想，將無限（情形）轉化為有限（三種情形），同時把一般情況轉化為特殊情況進行證明；在研究點與圓的位置關系、直線與圓的位置關系、圓與圓的位置關系時，我們也運用了分類思想；等等。當我們能主動將不同內容的研究方法聯系起來時，學習的難度便會降低，同時加強了不同知識之間的關聯，有利于建立富有邏輯關系的知識結構。

最后，我們要將圓與直線形的知識聯系起來。雖然本章是學習圓的知識，但呈現的圖形不單是一個圓，許多圖形是圓和直線形的組合。因此，我們要善于將與圓有關的問題進行轉化（化未知為已知，化復雜為簡單，化特殊為一般），并綜合利用直線形的知識解決問題，以提升我們的邏輯思維能力和解決問題的能力。

（作者單位：江蘇省南京市江寧區教學研究室）