基于假設法的高中化學解題應用分析

摘要：隨著科學教育的不斷發展，教育強調培養學生的邏輯推理、分析和創新思維能力.在此背景下，假設法作為一種有效的化學解題工具，在提高學生這些能力方面展現出了獨特的優勢.通過極端假設、賦值假設和過程假設等多種方式，將抽象的化學概念具體化，不確定的問題明確化，復雜的過程簡單化，極大地促進了學生在化學學科的深入理解和應用能力的提升.因此，深入研究和應用假設法在高中化學教育中具有重要的實踐意義，對于培養新時代學生的科學素養和創新能力起到了關鍵作用.

關鍵詞：假設法；高中化學；解題；應用

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2024）27-0124-03

在當前高中教育體系中，化學學科不僅僅是知識的傳授，更重要的是通過化學解題來培養學生的邏輯推理、分析及創新思維能力.假設法作為一種重要的解題技巧，在高中化學教學中扮演著至關重要的角色，其通過引導學生在解決化學問題時建立和驗證假設，幫助學生更深入地理解化學概念，提升解題能力.從極端假設法的具體化思維，到賦值假設法的明確化未知，再到過程假設法的簡化復雜問題，假設法的多種應用方式不僅使化學解題過程變得更加高效，而且促進了學生綜合思維能力的發展.因此，深入分析和探討假設法在高中化學解題中的應用，對于提高化學教育質量、培養學生的科學素養具有重要意義.

1假設法在高中化學解題中的作用機制

1.1有助于提升學生邏輯推理能力

假設法要求學生在面對化學問題時，基于已有的知識和信息建立合理的假設，然后通過邏輯推理過程驗證這些假設的可行性[1].假設法的運用，特別是在探討未知或復雜的化學問題時，能夠有效地指導學生從不同角度進行思考，促使其主動探索問題的多種可能性.這種主動探索和問題解決的過程，是對學生邏輯推理能力的直接鍛煉.

1.2有助于提高學生分析能力

假設法不僅要求學生掌握化學基礎知識和原理，還需要其在實際問題解析中運用這些知識進行深入分析[2].通過構建和驗證假設，學生能夠逐步分解化學問題，從而更加深入地理解化學反應的本質和機理.如在處理化學平衡問題時，學生需要分析反應物、生成物、反應條件等多個因素如何影響平衡狀態.通過假設法可以設定特定條件下的反應結果，進而分析實際觀察與理論預測之間的差異，找出原因并深化對化學平衡原理的理解[3].

1.3有助于培養學生創新思維能力

假設法激勵學生在面對化學問題時不拘泥于傳統的解題路徑，而是鼓勵學生基于已有知識構建新穎的假設，并探索其有效性[4].這一過程不僅是知識應用的實踐，更是創新思維能力培養的重要環節.此外假設法還可應用于探索未知化學現象，如在化學實驗中，學生通過對觀察到的現象提出假設，再通過實驗驗證，從而在探究過程中鍛煉創新思維.這種思維方式鼓勵學生主動探索化學世界的多樣性.2假設法在高中化學解題中的應用

2.1極端假設法，化抽象為具體

極端假設法的基本原理是在解題過程中設定某些條件至極限或極端狀態，以此為基礎進行問題的分析和解答[5].如當處理涉及濃度、壓力或溫度變化的化學平衡問題時，可假設其中一個因素達到極端值（如無限大或接近零），然后分析這種極端條件下系統的反應和變化.通過這種方式，學生能夠更直觀地看到各種化學參數之間的關系及其對反應的影響，從而更深入地理解化學原理.

極端假設法的應用能夠幫助學生從復雜的化學概念中抽離，通過極端化的條件簡化問題的復雜性，將難以捉摸的化學現象變得更加清晰易懂，還能培養學生的批判性思維和創新能力[6].在解題過程中，學生被鼓勵思考不同的假設條件下可能出現的各種情況，這不僅鍛煉了其思維靈活性，也促進了對化學知識的深入理解和應用.

例1給定50 mL、濃度為18 mol/L的硫酸溶液，加入過量的銅片后加熱一段時間，求反應后被還原硫酸的物質的量，選項為（）.

A.0.85 molB.不超過0.45 mol

C.超過0.45 mol且不足0.9 mol

D.0.9 mol

解答首先分析化學反應式，明確題目中涉及的硫酸和銅發生的是氧化還原反應Cu+2H2SO4（濃）CuSO4+SO2↑+2H2O.在此反應中，過量的銅片僅與濃硫酸發生反應，不會與稀釋后的硫酸作用.考慮到反應進行的時間和其他變量無法準確判定反應終止點，故采用極端假設法.假定所有硫酸均參與反應，則根據化學反應式推算，所消耗的硫酸量為初始濃度與體積的乘積，即0.9 mol.然而，這種情況在實際中不會全部發生，故真實被還原的硫酸量應在0.45 mol以下，故正確答案為B.

由此可見，極端假設法在高中化學教學中的應用，對于提高學生解題能力、深化化學知識理解，以及培養創新和批判性思維具有顯著作用.通過對極端假設法的系統訓練和應用，學生能夠在化學學習中取得更好的成效，為日后的科學研究和實踐打下堅實的基礎.

2.2賦值假設法，化不確定為明確

賦值假設法在高中化學解題應用中扮演著關鍵角色，此法通過為化學題目中的未知變量賦予特定值或范圍，將不確定性轉化為明確的數值問題，從而簡化解題過程并提高準確率.這種方法特別適用于那些涉及多個變量、條件復雜的化學題目，如化學反應的量的關系、溶液的濃度計算等.通過為某些變量賦予特定值，可以將復雜的化學問題轉化為簡單的數學運算，學生能夠更加集中地分析關鍵因素，從而快速找到問題的解決方案.在高中化學教學中，賦值假設法不僅能夠幫助學生提高解題效率，還能夠加深其對化學概念的理解.

例2觀察硝酸銀與碘化鉀溶液的反應過程中，當反應停止，反應后的溶液質量與反應前的碘化鉀溶液質量相等.為了分析所添加硝酸銀溶液的質量分數，需要進行深入探究.要求：闡述反應原理，計算出硝酸銀溶液的質量分數，并給出相應的解釋.

解答解題過程中由于題目未給出具體數值，要確定碘化鉀的質量百分比，需采用賦值技巧以實現定量分析.分析得知，此題涉及的反應是KI+AgNO3AgI↓+KNO3.假設反應中碘化鉀的物質的量，為1 mol，則消耗的硝酸銀的質量為170 g.依據題意反應后溶液的總質量與反應前相同，因此加入的硝酸銀溶液質量等同于析出的碘化銀質量，即235 g.據此可計算出硝酸銀的質量百分比為ω=170/235×100%，結果約為72.34%.通過這一解題實例可以看出，在高中化學解題中運用假設法不僅拓展了思維，也有效應對了解題時的各種情境.

由此可見，在探討反應物與生成物的量的關系時，通過對反應物量的賦值，學生可以直觀地看到不同反應物量如何影響生成物的產量，進而更深入地理解化學計量學原理.此外，賦值假設法也培養了學生的邏輯思維和解決問題的能力，使其在面對復雜的化學問題時，能夠靈活運用知識，有效進行分析和推理.因此，賦值假設法作為一種高效的化學解題工具，在高中化學教育中具有重要的應用價值，對于提高學生的學習效率和化學思維能力都具有顯著的促進作用.

2.3過程假設，化復雜為簡單

過程假設法在高中化學解題應用中，是將復雜化學反應或過程分解為更易于理解和處理的簡單步驟的一種有效策略.這種方法要求學生在面對包含多個階段或因素的化學問題時，不是一次性解決整個問題，而是將問題拆解成若干個小的、可管理的部分，逐一進行假設和驗證.如在處理涉及多步化學反應的題目時，學生可以假設每一步反應單獨發生，分別分析每一步的可能結果，最終再綜合考慮所有步驟的影響，從而得出結論.這種方法使得原本復雜的化學問題變得清晰可控，學生可以更加專注于每一個具體步驟，有效避免在解題過程中的混淆和錯誤.

例3已知在一定溫度下，固定體積的封閉容器中存在反應2NO2N2O4，在第一次平衡時，NO2的轉化率為a，氣體總壓強為p.隨后，再加入1 mol的NO2，系統再次達到平衡.要求分析并確定第二次平衡時NO2的轉化率b與第一次的轉化率a的關系，以及氣體總壓強p′與2p的關系.

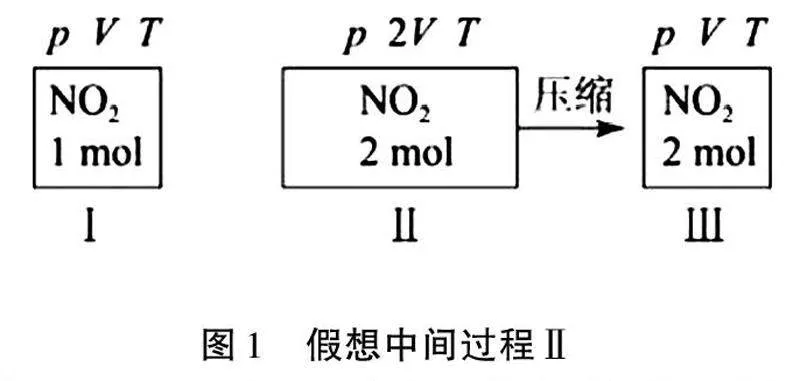
解答為了解決這個問題，采用過程假設的方法.考慮到化學平衡的狀態與反應條件和初始反應物的量有關，而與達到平衡的路徑無關.因此，設想一個假想的中間過程Ⅱ，如圖1.

解答過程Ⅰ與Ⅱ等效，在保持容器體積不變的情況下，向其中注入1 mol的NO2，當系統達到平衡時，NO2的轉化率為a.若在同一容器中再次加入1 mol NO2直至平衡，其效果與一開始就向容器中注入2 mol NO2相同.若對過程Ⅱ的容器施加壓力，將其體積減小到原來的一半，這將與過程Ⅰ的條件相等.考慮到2NO2N2O4的平衡反應，增加壓力會使平衡向生成物方向移動，從而NO2的轉化率增加，因此b大于a.按照同樣的邏輯，可以推斷出2p大于p′.

由此可見，在高中化學解題過程中，假設法的應用具有重要意義.首先，有助于學生更準確地理解化學反應的整體過程和機理，尤其是在面對那些步驟復雜、涉及多個反應物和產物的題目時；其次，通過將復雜過程分解為簡單步驟，學生的解題思路更加清晰，能夠更有效地組織和處理信息，從而提高解題的準確性和效率.此外，過程假設法還能夠培養學生的邏輯思維和問題分析能力，使他們在化學學習中形成系統化、條理化的思維方式.

3結束語

在探索高中化學解題策略的過程中，假設法展現了其在提升學生邏輯思維、分析能力和創新能力方面的獨特優勢.假設法不僅優化了化學解題過程，也為學生提供了一個全面、深入理解化學原理的平臺.這種方法的應用對于高中化學教育具有重大意義，能夠有效地激發學生的學習興趣，提高學生的綜合科學素養，為未來的科學研究和職業發展奠定堅實的基礎.因此，將假設法融入高中化學教學是一種值得推廣的有效教學策略.

參考文獻：

［1］ 云建禮.高中化學解題中假設法的應用[J].數理化學習（高一二版），2022（4）：59-60，64.

[2] 黃阿倩.高中化學實驗探究式教學模式的構建深析[J].互動軟件，2022（6）：579-580.

[3] 劉敏.假設法在高中化學解題中的應用分析[J].文理導航，2022（17）：64-66.

[4] 李明.假設法在高中化學解題中的應用研究[J].中學生數理化（學習研究），2022（12）：70-71.

[5] 陳艷.例析假設法在化學解題中的應用[J].數理化解題研究，2022（10）：125-127.

[6] 謝海龍，付旭偉.“證據推理與模型認知”核心素養的培養：以有機推斷與合成類試題的解答為例[J].高中數理化，2022（20）：51-52.

［責任編輯：季春陽］