邏輯推理素養視角下高考試題分析及教學建議
摘要:以2023年高考數學試題為研究對象,基于試題題型和試題內容兩個方面,對試題中考查的邏輯推理素養水平進行量化分析,探索高考命題規律,提出教學建議.
關鍵詞:邏輯推理素養;高考數學試題;教學建議
中圖分類號:G632文獻標識碼:A文章編號:1008-0333(2024)27-0030-03
通信作者:*常健(1975.7—),女,陜西省榆林人,碩士,副教授,從事數學教學研究.
《普通高中數學課程標準(2017年版)》(以下簡稱《標準》)提出數學學科核心素養涵蓋數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析六種[1].邏輯推理素養在整個數學體系的構建中占有重要地位,數學教學應全面、準確地把握邏輯推理素養的內涵和實質,以學生對數學概念理解和數學方法的運用為抓手,有意識地培養學生的邏輯推理素養.
1邏輯推理素養水平的劃分
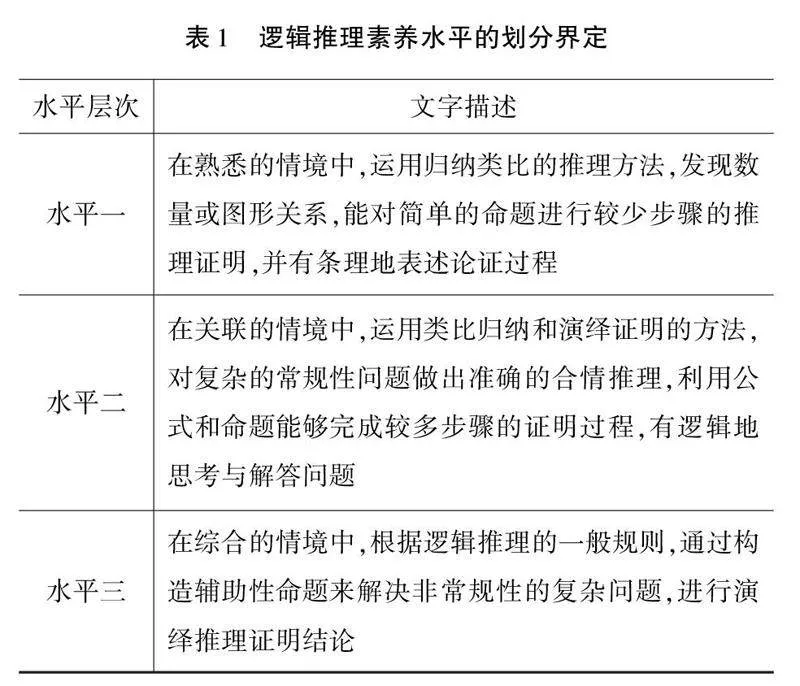
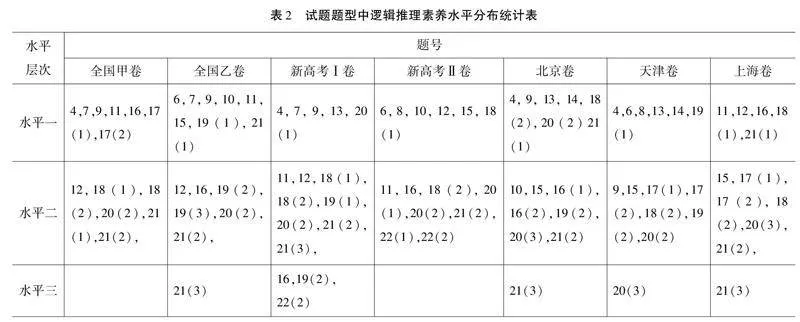
《標準》對數學學科核心素養的界定進行說明,提出邏輯推理是指從簡單命題出發,依照一定的規則推導得出結論,主要包括合情推理和演繹推理兩種類型.《標準》對邏輯推理素養劃分了三種水平,并用文字進行闡述[2],見表1.
依照劃分標準,舉例說明邏輯推理素養“水平”的確定.
例題(全國乙卷理21)已知函數f(x)=(1/x+a)ln(1+x).(1)當a=1時,求曲線y=f(x)在點(1,f(1))處的切線方程;(2)是否存在a,b,使得曲線y=f(1/x)關于直線x=b對稱,若存在,求a,b的值,若不存在,說明理由;(3)若f(x)在(0,+∞)存在極值,求a的取值范圍.
分析(1)本題考查導數的幾何意義,只要確定切線斜率和切點坐標,在熟悉的情境中進行簡單推理便可解決問題,考查邏輯推理素養水平一;(2)考查函數的性質,屬于含參函數的常規性問題,利用函數對稱性和特殊值法進行較多步驟的演繹推理,求解參數的值并進一步驗證結果,主要考查邏輯推理素養水平二;(3)考查函數與導數的關系,構造輔助函數,通過演繹推理證明結論,主要考查邏輯推理素養水平三.
2高考試題中邏輯推理素養水平的考查分析
選取2023年高考數學全國甲卷(理)(以下簡稱“全國甲卷”)、全國乙卷(理)(以下簡稱“全國乙卷”)、新高考Ⅰ卷、新高考Ⅱ卷、北京卷、天津卷,上海卷共計 7套試卷作為研究對象,從試題題型和試題內容兩個方面分析2023年高考試題的命題特點及考查情況.
目考查邏輯推理水平一,表現為學生能夠從常規命題中發現解題思路,只有新高考Ⅰ卷考查了水平三.
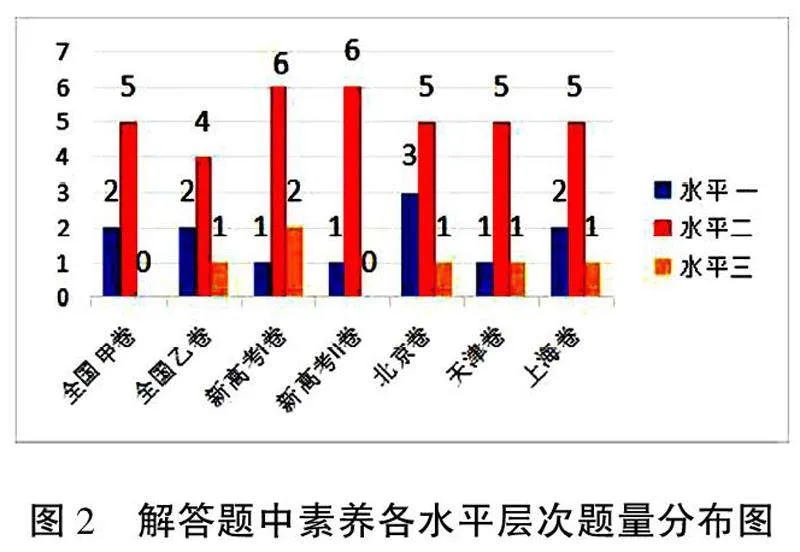
如圖2,7套試題的解答題考查邏輯推理素養水平二的題量最多,其次是水平一,水平三較少,解答題注重考查學生的邏輯思維能力和推理驗證能力,需分析和轉化問題,化難為簡,全國甲卷和新高考Ⅰ卷未考查邏輯推理水平三.
2.1高考試題邏輯推理素養水平的考查
本文整理了2023年高考數學7套試題中考查學生邏輯推理能力的題目,將每道解答題內涵蓋的小題作為單獨題目進行統計,并參照標準劃分水平,結果見表2.
2.2基于試題題型的邏輯推理素養水平考查分析
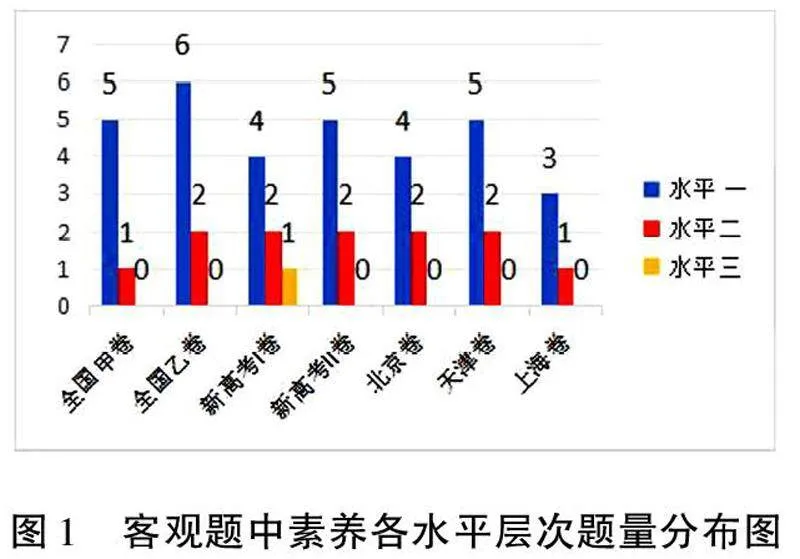
對表2進行整理,將試題中客觀題和解答題涉及的邏輯推理素養水平的考查題目分別進行頻數統計,得到圖1和圖2.
如圖1,7套試題的客觀題考查題量較多的為邏輯推理素養水平二,主要表現為在常規的情境中能利用公式性質對一般命題概念進行簡單推理,其次是每套試卷客觀題中均有1~2個題
2.3基于試題內容的邏輯推理素養水平考查分析
《標準》提出高中數學課程內容包括預備知識、函數、幾何與代數、概率與統計、數學建模與數學探究活動五大主題[3],對于預備知識中的內容考查形式基本固定,涉及邏輯推理較少,所以本文選取高考試題中函數、幾何與代數、概率與統計三部分內容對學生邏輯推理能力的考查情況進行分析.
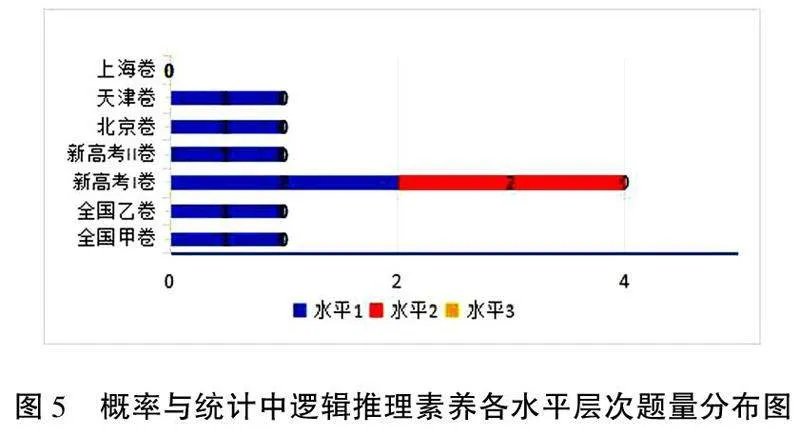
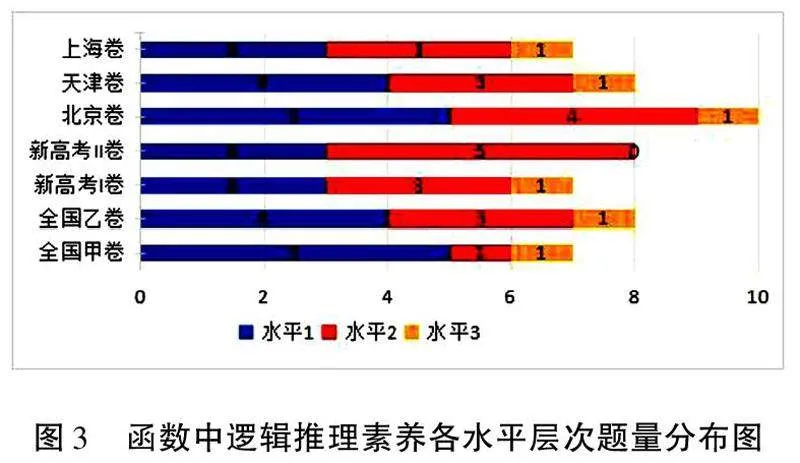
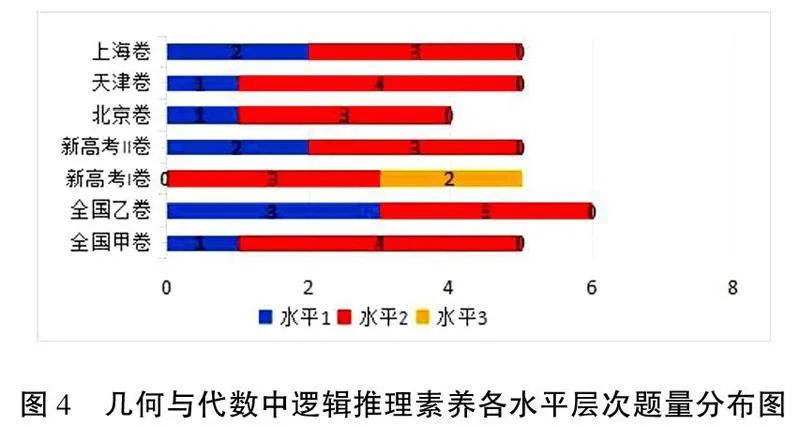
對表2進行整理,將試題中函數、幾何與代數、概率與統計內容涉及的邏輯推理素養水平的考查題目分別進行頻數統計,得到圖3、圖4和圖5.
如圖3,7套試題中除了新高考Ⅱ卷外,其余試題對于函數的考查均涉及邏輯推理素養三個水平的考查,并且每套試卷對于水平一和水平二的考查題量均保持在3~5道.可見高考中對于函數知識的考查難易結合,不僅要夯實基礎,也要有較高的歸納分析和構造轉化能力.
如圖4,7套試題對于幾何與代數考查邏輯推理素養水平二的題量最多,對學生的推理驗證能力的要求較高,只有新高考Ⅰ卷考查了水平三.
如圖5,7套試題對于概率與統計整體考查的題量較少,問題較為簡單,利用公式簡單推理便可解決問題,上海卷無邏輯推理素養的考查.
3結論與建議
3.1結論
高考數學命題注重理性思維素養,7套試卷從試卷題型來看,客觀題是基于學生對數學概念公式和性質定理的認識,考查學生分析綜合和歸納類比的能力,題目多為對邏輯推理水平一的考查;解答題考查形式基本固定,考查知識的聯系和運用,需演繹證明,主要考查水平二,對學生的邏輯思維能力要求較高,同時重點在解答題中考查.從試卷內容來看,函數、幾何與代數、概率與統計的考查均基于邏輯推理素養水平一和水平二的考查,注重知識基礎,同時函數內容考查邏輯推理的題量多且水平廣.
3.2建議
在教學實踐中,教師可結合高考命題規律進行針對性教學,讓學生在數學實踐與應用中逐步提升邏輯推理核心素養.基于上述結論,提出以下教學建議.
第一,夯實基礎,拓展拔高.教師在日常的教學中,給學生提供熟悉情境下的簡單問題,激發學生對數學學習的興趣,使學生化被動的數學學習為主動的邏輯推理過程,滲透學生對數學基礎題型的認識,掌握基本概念定理.對于復雜的數學問題,注重提問的啟發性,引導學生大膽猜想和演繹證明,鼓勵學生勇于探索,形成嚴謹的邏輯思維.
第二,分層設計,針對訓練.在日常學習中,教師需重視對函數知識的講解與練習,要讓學生做到扎實基礎,學以致用,舉一反三.同時,要重視解答題的訓練,要明確解題思路和步驟,讓學生能夠有條理地處理實際問題,形成完善的推理思維.
第三,運用方法,提高素養.在數學概念的教學中,教師可借助實際物體,將抽象的數學概念具象化,夯實學生的底層邏輯,引導學生積極參與數學探究活動,鍛煉學生的邏輯思維.在解題過程中,啟發學生找出已知和未知的聯系,引導學生聯想與類比,體會分類與整合的方法,體會“化整為零”的思想,從而提高學生的邏輯推理素養.
參考文獻:
[1] 李海東.基于發展學生核心素養的初中數學教學[J].中國數學教育,2019(7):3-8,13.
[2] 劉凱莉.邏輯推理素養視角下的高考試題研究[D].長沙:湖南師范大學,2021.
[3] 謝發超,原坤.SOLO分類理論視域下高考數學試題思維層次分析:以2023年全國新高考Ⅰ卷為例[J].中國數學教育,2024(2):46-49,56.
[責任編輯:李璟]

