基于核心素養的中職數學解答題命題分析


摘要:本文收集近五年福建省中等職業學校學業水平考試和各地市的統考題目,對知識點和數學核心素養進行分析,結合學生實際學情,研究教材幾個章節知識點之間的聯系,并對幾道典型的例題進行側重分析.
關鍵詞:中職數學;學業水平考試;解答題;命題分析
中圖分類號:G632文獻標識碼:A文章編號:1008-0333(2024)27-0015-03
《福建省中等職業學校學生學業水平考試公共基礎知識考試大綱》提出,中等職業學校數學學科核心素養主要包括:數學運算、直觀想象、邏輯推理、數學抽象、數據分析和數學建模[1].作為福建省中等職業學業水平考試(以下簡稱“學考”)文化課數學科目的重要組成部分,解答題看似簡單,實則暗藏玄機,對福建省的中職考生來說,最頭疼的莫過于二卷的解答題,很多題目無從下手.
為幫助中職學生更好地準備考試,發展數學思維,本文對福建省歷年的數學學考真題進行統計分析,以此達到鞏固學生數學核心知識、落實數學方法的目的.
1試卷分析
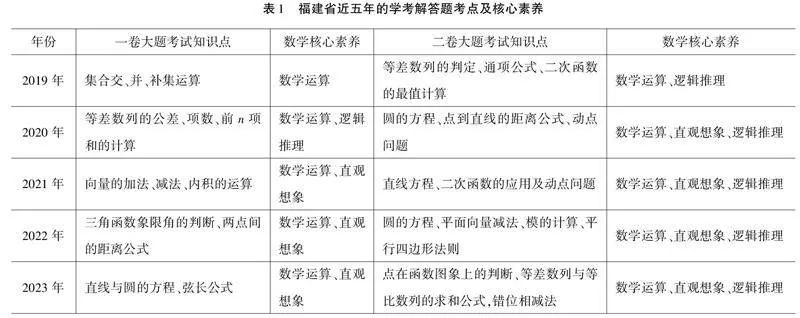
作為一名扎根于一線教學的中職數學老師,每年都進行學考的教學工作,見證一批批學子從備考到應考的過程,也經歷了學考由簡到繁、由易到難的整個歷程.表1統計了福建省近五年的學考真題和福建省各地市的考卷,分析知識點及考查的數學核心素養等,具體詳情見表1.
在近五年的學業水平考試中,解答題的考查范圍集中在二次函數、數列、向量和直線與圓的章節中.通過對比年份之間的差異,我們可以發現,無論是一卷還是二卷,考試的知識點正在由單一知識點過渡到多個知識點,考查的數學能力由簡單的數學計算、歸納演變到邏輯推理、圖形分析和數值計算.很顯然,這場考試的難度正在逐年提高.
針對近年考試熱點,教師需要培養學生在學會知識的基礎上融會貫通,綜合應用不同章節的知識解決問題.如何高效地解決不變的課時與日益增長的綜合性問題,是本文要研究的主要內容.
2研究內容
一方面,由表1可以發現,在福建省歷年學業水平考試的數學學科的考題中,解答題對于數學運算和直觀想象兩個方面核心素養有較多次的考查;另一方面,分析福建省當下使用的中等職業數學教材,以最新的學業水平考試標準要求,分析章節中的知識點以及它們之間的聯系.從數學運算與直觀想象兩個角度展開知識點分析,可得到表2、表3.
由上述的兩個表可以發現:很多考題同時要求學生掌握數學運算和直觀想象這兩個核心素養,二者早已密不可分,難舍其誰.對于學生來說,最難的部分在于如何構建這兩個核心素養的橋梁,達到融會貫通的目的;對于教師而言,在解題過程中培養學生數形結合的數學思想,養成幾何和代數問題相互轉化的數學方法,是接下來教學中要著重解決的地方.
3教學建議
基于以上教學目標,筆者提出以下幾點教學建議,用于平時教學推進落實.
(1)在講授新課時,可以從多個角度引入知識,培養學生圖形觀察和數學計算能力,突出知識點的關鍵性質和本質問題;
(2)在解答問題時,鼓勵學生勤動腦,在觀察圖象中分析圖中的數量關系,并轉化成代數式;分析圖表和圖形,學會用代數式表達不同的變量關系,獲得精準的答案;
(3)教師在習題課上,要抓住本質問題,進行變式訓練,有意識地歸納、總結相似知識點;
(4)在數學運算和直觀想象中滲透數學邏輯推理方法,不斷提升學生分析問題的能力,鼓勵學生一題多解,從“數”“形”兩個緯度分析問題,構建多種方式的解題思路;
(5)加強錯題本的利用,在課后幫助學生養成歸納總結知識的學習習慣;
(6)收集普高的習題、學考的真題和福建省各地市的解答題,對學生定期進行訓練,培養學生思維的靈活性和創新性,發展數學推理和計算能力.
4經典例題
例1(2022年廈門市質檢)已知點A(-1,1),點B(4,0),在第一象限內存在點C(1,m),使得AC⊥BC.
(1)求向量BA的坐標;
(2)求m的值;
(3)求sin〈BA,BC〉+cos〈BA,BC〉的值.
分析本題在平面直角坐標系中,應用了向量的知識,第(3)問考查了銳角三角函數的知識,結合第(1)問的結論,學生可以應用內積解決問題,計算量大,也可以應用直角三角形的性質解決問題.本題對學生觀察能力要求高.兩種方法都鍛煉了數學運算能力,是一道不可多得的好題.
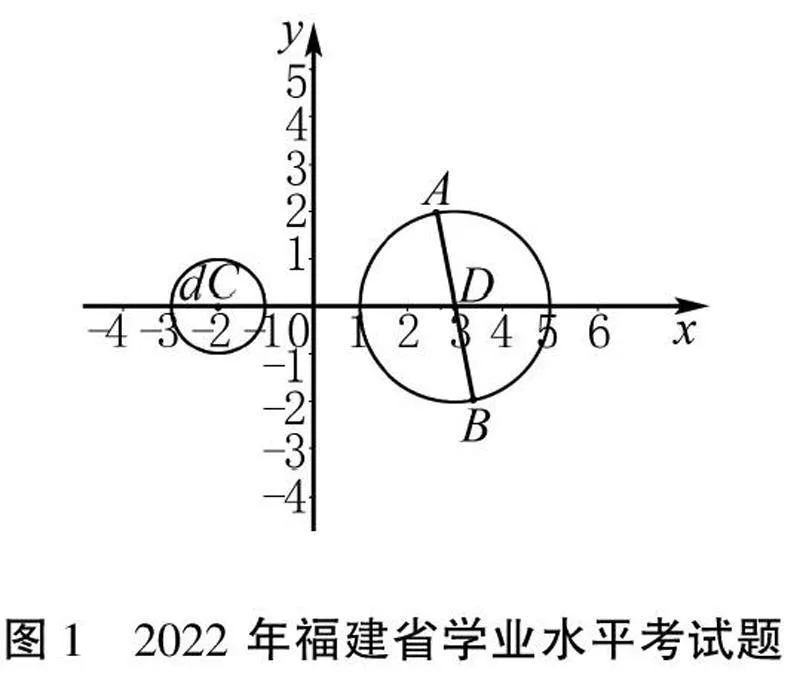
例2(2022年福建省學業水平考試)如圖1所示,已知圓C:(x+2)2+y2=1,圓D:(x-3)2+y2=4,P(x,y)為圓C上的動點,AB恒為圓D的直徑.
(1)寫出圓D的圓心和半徑;
(2)求PA-PB的值;
(3)求PA+PB的最小值.
分析本題在圓的基礎上考查了向量的加法、減法和模的運算知識.學生比較容易解決前兩個問題,第(2)問在進行向量的減法運算以后,還考查學生對向量的模的掌握情況;第(3)問是動點問題,顯然需要觀察圖象,要求學生有較強的觀察能力,又用到了平行四邊形法則、平行四邊形的性質和向量的模長知識.本題考查了學生對數形結合、邏輯推理和數量分析等多種數學能力的綜合應用.
例3(普高練習題改編)在公比為q(q>0)的等比數列{an}中,已知a=2,且-4a,1/2a,3a-12成等差數列.
(1)求等比數列的公比q ;
(2)求該等比數列的通項公式 an;
(3) 若滿足loga≥4,求n的取值范圍.
分析第(1)問考查了學生對于等差數列性質的應用,重點考查計算能力;第(2)問考查了等比數列的知識,根據題意可求出一個等比數列的通項公式;數列作為特殊的函數,第(3)問考查了對數的計算法則和不等式的求解.這道題結合了三個不同的知識點,每一小題都對學生的運算能力提出了較高的要求.
5結束語
在解決函數、數列、直線與圓的三種位置關系的相關問題時,追根究底,要求學生結合圖形找到對應的位置關系,并轉化為數量關系[2].由于本人研究能力有限,通過網上查找相關的資料,收集的案例可能不夠全面,今后筆者將繼續收集相關題型資料,不斷完善該知識體系,提高教學效率,構建知識體系,幫助學生更好地運用直觀想象分析問題.希望本文對一線執教的中職數學老師有所幫助.
參考文獻:
[1] 福建省教育廳.福建省中等職業學校學業水平考試《公共基礎知識》考試大綱[EB/OL].(2024-01-18)[2024-03-12].https://jyt.fujian.gov.cn/xxgk/zywj/202401/P020240118349932794744.pdf.
[2] 李士榮.中職“直線與圓錐曲線”專題解題分析[J].數理化解題研究,2021(04):18-19.[責任編輯:李璟]

