挖掘“圓錐曲線”本質 培養高中生數學核心素養

摘要：課程改革背景下，培養核心素養是高中數學教學的最終目標.對于圓錐曲線問題，要根據問題求解需求，建立坐標系，按照幾何圖形特點運用轉化思想，將幾何問題轉化為代數問題.文章簡要介紹圓錐曲線中蘊含的思想及育人價值，并結合圓錐曲線教學實踐，探討核心素養的落實策略.

關鍵詞：高中數學；圓錐曲線；核心素養；培養策略

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2024）27-0040-03

在高中數學教學過程中，基于直線和圓方程展開圓錐曲線內容學習，要求學生能夠掌握坐標法解決幾何問題的方法，感受平面解析幾何蘊含的思想.通過教學活動設計，培養學生數學建模、運算、推理等方面的能力，最終提高他們的核心素養.

1圓錐曲線蘊含的價值分析

圓錐曲線也稱“二次平面曲線”或者“圓錐截面”.在數學發展過程中，笛卡爾提出解析幾何這一概念，自此，解決解析幾何問題時，圓錐曲線成為重點學習內容，在高考中，圓錐曲線也是重要考點.隨著科技的發展，社會需求也逐漸發生變化，數學家、天文學家在各自領域研究成果顯著.開普勒通過對行星運行軌跡的研究，發現軌道為橢圓形；牛頓計算出天體運動軌道同樣為橢圓形；伽利略得出拋擲物體會得到拋物線.圓錐曲線和以上內容聯系緊密，通過圓錐曲線的研究，能夠促進天文、物理等學科發展.笛卡爾統一了代數和幾何知識，將解析幾何體系創立起來，將幾何問題進行轉化變為代數問題求解.

數學學科素養要求下，圓錐曲線內容十分重要，其內容豐富，包括拋物線、雙曲線以及橢圓等知識.在教學過程中，教師要重點培養學生運算、推理等方面能力，深入挖掘圓錐曲線這一章節當中的數學思想，強化學生的抽象思維.針對圓錐曲線的幾何特征教學，教師可以利用數學實驗、實際問題等作為載體，將圓錐曲線幾何特征提取出來，通過實驗組成要素，將其轉化成數學現象.這一過程也是數學抽象過程，對于學生運算素養、推理能力、邏輯思維的培養十分有利[1].

根據圓錐曲線內容，結合本章節知識教學要求，從圓錐曲線的發展史、內涵等角度，將教學內容進行適當調整，授課過程中滲透數學問題解決應用思想及方法，深度思考所學內容.學生在思考期間自主生成知識，形成數學思維，達到核心素養要求.解析幾何屬于方法論的一種，典型的就是坐標法.應用此方法就是應用轉化思想，將幾何問題變成代數問題，建立坐標系作為轉化思想應用的載體，利用坐標和方程解決問題，運用推理思維、代數運算，得出代數結果，反映幾何性質，提高學生解決問題的能力[2].

2培養高中生數學核心素養的策略

解析幾何教學過程中，教師要注重引導學生思維，引領學生研究和分析幾何問題，按照問題組成幾何要素分析其幾何性質，運用代數方式表達幾何問題，得出幾何結論.以下選擇蘇教版高中數學教材“橢圓的標準方程”一課教學為例，探討運用圓錐曲線培養學生核心素養的幾點策略.在核心素養教學目標之下，教師要兼顧知識技能、數學思想、數學文化、數學方法等方面指導，促進學生核心素養生成.本節課教學目標設定如下：第一，知識技能目標，能熟練掌握橢圓概念，了解橢圓幾何特點，利用推導方式，將標準方程推出，明確方程參數的幾何意義，反過來，利用標準方程來判定其是否為橢圓，掌握焦點坐標；第二，過程和方法目標，學生能夠根據橢圓的幾何特點，推導出其定義，在探究交流階段經歷抽象的過程，明確橢圓的幾何特點，即具有對稱性，以此建立合適的直角坐標系，利用代數的方法推導標準方程，提高運算能力及素養，利用橢圓習題進一步鞏固橢圓領域知識；第三，情感態度價值觀目標，學生經歷數學實驗過程，直觀觀察橢圓圖形特點，分析特征，總結幾何概念，參與標準方程的推導過程，體會轉化思想的應用過程，感受數學方法和思想學習的重要性[3].

2.1啟發導入，設問引導

導入環節，教師可以引入古希臘的故事創設教學情境：“某小島統治者開鑿出一個巖洞監獄，形狀為橢圓形，被關押犯人時常商討出逃計劃，可是計劃很快被發現，犯人們之間相互猜忌，認為有同伴叛變，實際上內部人員并沒有叛變，而是犯人商議事情的位置在橢圓焦點上，看守人員處于另一焦點，此時即使犯人聲音較小，聲音經過墻壁反射以后也會被看守人員聽到”.根據以上故事，引入生活當中和橢圓相關的圖片，根據圖片提出問題“結合光反射路線，有怎樣的結論？”“如果一個籃球被放在桌面上，受到一束平行光的照射，籃球投影輪廓可能有怎樣的變化？影子輪廓上多點到地面切點和籃球之間距離的變化是怎樣的？”選擇生活當中學生熟悉的場景，啟發其思考數學問題，學生利用生活經驗，結合實際觀察，可以總結出“光能聚焦，經過反射以后，產生橢圓的形狀”.同時，通過觀察得出結論，即橢圓一共有兩個焦點，如果光線從橢圓其中一個交點射入，利用鏡面聚焦之后，光線可以匯集在另一個焦點上，此時光線長度相同，也就是籃球受到正上方的光照以后，可以形成圓形的輪廓，球與地面相切的點即為圓心，所有輪廓上的點到切點的距離都是一個常數，所以，可以得出結論，光線傾斜地照射籃球的時候，產生的影子輪廓就是橢圓，此時橢圓上的點至切點的距離可跟隨點位置不斷變化.利用趣味故事和生活情境，配合問題引導，讓學生對橢圓知識形成初步感知.

2.2問題探索，新知抽象

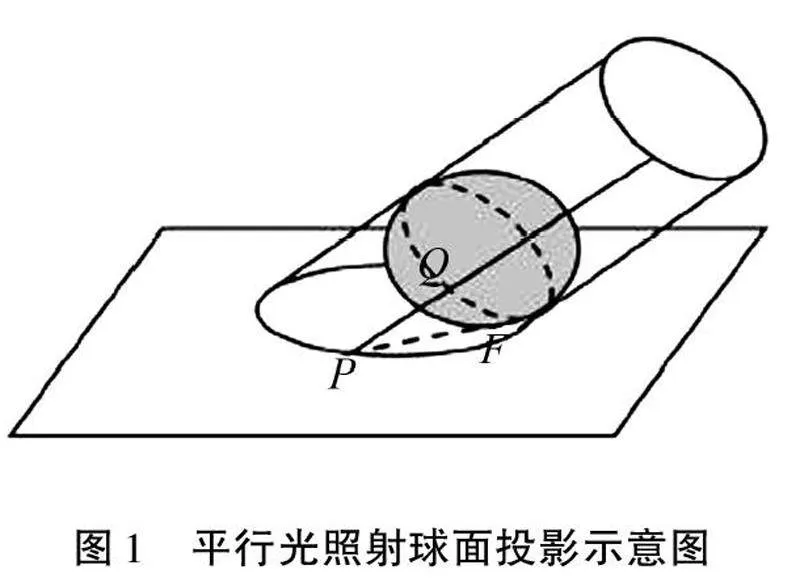
在課堂上，為了幫助學生抽象新知，教師可以設計探究學習任務，給出平行光照射球面的圖形，創設教學情境，設置問題“若將平行光線視為圓柱面，其與球面相切，則橢圓和圓柱關系是怎樣的？”引領學生思考，使其運用抽象思維進行觀察，將籃球抽象為球形，對面抽象為與球面相切的面，這時平面與柱面的相交線就是橢圓.為體現課堂教學教師的引導性，教師繼續設置探究任務“如圖1所示，當球與平面相切于點F的時候，點P在橢圓上，且點P在母線上，球與橢圓相切，切點是Q.如果點P為動點，隨著點P的移動，PF和PQ會有怎樣的變化？如何移動才能得到圖1？點P運動期間，圖中的長度關系是怎樣保持不變的？”

根據橢圓的對稱性思考“圖1中的橢圓可以通過怎樣的方式得到？”“點P運動過程中，長度關系的不變性是怎樣的？”根據圖形對稱性，引導學生利用拼接的方式在平面下方補充完整，或者將另一側看作為相同大小的球體，和平面保持相切.假設切點是E，經過點E母線和球之間相交于點M，那么PE=PM，PF=PQ，PM+PQ=MQ，即定長，進而得出PE與PF之和為定長.此時，學生即可了解“橢圓上的點至兩定點間距離為常數”.教師繼續提問“若用不平行于底面的平面截取圓柱，可以得到怎樣的圖形？截面當中是否有兩個定點距離為一個常數？”以探究問題啟發學生思考橢圓特征，學生可以直觀了解到橢圓截線的定義，即不與底面平行的截平截圓柱得到的圖形即為橢圓，如果在截面的上方和下方畫出同樣大小的球，使其與截面保持相切的狀態，得到的切點就是所求定點.教師可以利用技術手段去掉圓柱、球等，幫助學生抽象出橢圓圖形及其特征，輔助學生掌握橢圓的定義.在任務驅動和提問啟發的環境之下，師生共同對橢圓定義進行總結，就是“處于平面之內，到兩個定點距離的和等于定長度的所有點的軌跡，其中定點即為焦點，兩焦點距離就是橢圓的焦距”.為了讓學生理解焦點名稱，可以展示生活中的事例，如播放電影時，燈泡反射的鏡面屬于橢圓面，所有從定點發出的光線都可向另一定點聚焦.在教學過程，引入光學、聲學等傳播問題，幫助學生感受橢圓的幾何特點，運用抽象思維思考球切線相關知識，形成抽象思維，提高邏輯推理能力和抽象素養，學會利用數學思維思考圓柱、球和截面三者之間的關系.

2.3擴展新知，類比探索

為培養學生的類比思維，在課堂上，教師可以帶領學生回憶直線和圓等方程求解的一般步驟，調動其以往學習經驗，學生思考以后，回答“先建立坐標系，將動點坐標設出，之后列出幾何等式，將坐標代入，經整理和化簡得出結果”.教師此時要做好引導工作，提出問題“通過學習，同學們已經掌握了橢圓的特點，那么直角坐標系的建立方式有哪些？選擇哪種坐標系進行計算相對簡單？”基于問題引領，學生深度思考，計算時可將坐標軸選在焦點所在直線，通過作焦點線段的中垂線，完成坐標系建立，不但坐標表達簡單，而且符合圖形對稱特點，設出點坐標以后，根據橢圓定義化簡方程.如果運用移項平方的方式化簡，也可以得到橢圓的方程.橢圓方程當中存在三個量，即a，b，c都是正數，“是否能夠從橢圓當中找到代表線段？”以問題為載體，指導學生探究不同量的幾何含義.在類比思想的運用之下，學生順利寫出焦點在y軸上的標準方程，之后對比觀察焦點、標準方程，分析二者之間的關系.經過仔細觀察可知，標準方程中，哪個坐標軸所對應分母大，橢圓焦點就在此坐標軸上.將橢圓的標準方程引入，結構更簡潔，學生可以體會到數學的對稱美和簡潔美，運用數形結合思想，形成直觀想象能力，提高核心素養.

2.4及時總結，鞏固提升

在總結階段，教師可以通過問題引導及習題設計的方式輔助學生理解.問題為“橢圓定義當中有哪些注意事項？”“橢圓標準方程的推導，要依據怎樣的方式建立聯系？”“推導橢圓方程及方程化簡過程你有哪些感想？”“根據方程判斷幾何圖形是否為橢圓，若是，則將其轉化為標準方程，當a，b，c的值能確定之后，求橢圓的焦點坐標”.教師設計作業任務，學生根據問題判斷，在解決問題時經歷從“數”到“形”的過渡，對標準方程形成深刻的認識.通過對比分母大小，確定焦點位置，將a，b，c值求出，求出焦點的坐標，深化學生對橢圓定義及焦點的理解.針對含有參數的方程，學生精準判斷是否為橢圓的標準方程還有困難，因為參數取值不同，曲線形狀的變化也各有不同，通過反復練習有助于學生內化分類討論思想，提高其核心素養[4].

3結束語

綜上分析，在高中數學圓錐曲線內容教學過程中，教師要深挖內容蘊含的思想和教育價值，引領學生學習，體會圓錐曲線在解決問題中的重要性，依托各類教學活動作為載體，引領學生參與知識探究，在學習過程中，感受其中蘊含的數形結合思想，最終提高數學核心素養.

參考文獻：

［1］ 趙家早.問題引領，追求本質，讓數學核心素養的培育落地：以“圓錐曲線的離心率問題”專題復習為例[J].中學數學月刊，2020（5）：22-24.

[2] 陳言.基于數學教學主題培養數學核心素養：以“再探圓錐曲線的離心率”教學為例[J].福建基礎教育研究，2019（7）：57-58.

[3] 陳新滎.基于數學核心素養，培養高中數學閱讀能力：“圓錐曲線的光學性質”教學設計[J].中小學數學（高中版），2018（3）：14-15.

[4] 耿曉紅，郭守靜.基于數學抽象核心素養，引導學生變式探究：以一類圓錐曲線定值問題探究為例[J].中學數學教學參考，2019（10）：4.

［責任編輯：李璟］