多種方法解答平均數問題

小朋友，在生產和生活中，我們經常會遇到計算平均數的問題。如何解答這類問題呢，下面和我一起來學習吧！

一、常規解法

常規解法就是用計算平均數的基本數量關系式來解答，應記住這些數量關系式：平均數=總數量÷總份數，總數量=平均數×總份數，總份數=總數量÷平均數。

例題1 在一次數學測試中，前5 名學生的成績分別是99分、98分、97分、96分、95分。這5 名學生的平均成績是多少？

可根據“平均數=總數量÷總份數”計算這5名學生的平均分。這5名學生的分數總和是99+98+97+96+95=485（分），平均成績是485÷5=97（分）。

例題2 某鑄造廠接到一份生產零件的訂單，用6 天的時間完成了生產任務。鑄造廠前3 天共生產了168個零件，后3 天平均每天生產52個零件。鑄造廠平均每天生產多少個零件？

先算出鑄造廠后3天生產了52×3=156（個）零件，再算出鑄造廠生產零件的總數是168+156=324（個），最后根據“平均數=總數量÷總份數”算出鑄造廠平均每天生產零件324÷6=54（個）。

二、基數法

在計算一組數據的平均數時，可先找出這組數據中最小的數（或最大的數），選取最小的數（或最大的數）作為這組數據的基數，算出其他所有的數與所選基數的差，然后算出這些差的總和，再用算出的總和除以這組數據的個數得到商，最后用所選的基數加上（或減去）商，得到的結果就是這組數據的平均數。

例題3 某筑路隊用4 天的時間修了一條公路，第一天修了1320米，第二天修了1350米，第三天修了1360米，第四天修了1370米。這個筑路隊平均每天修公路的長度是多少？

筑路隊修公路長度的最大數是1370，最小數是1320。

如果選最小的1320作為基數，先算出余下各數比1320大多少，1350-1320=30（米），1360-1320=40（米），1370-1320=50（米），再用這些差的總和除以這組數據的總個數得到商，商是（30+40+50）÷4=30（米），最后用基數加上商，得出這個筑路隊平均每天修公路1320+30=1350（米）。

如果選最大的1370作為基數，先算出余下各數比1370少多少，1370-1320=50（米），1370-1350=20（米），1370-1360=10（米），再用這些差的總和除以這組數據的總個數得到商，商是（50+20+10）÷4=20（米），最后用基數減去商，得出這個筑路隊平均每天修公路1370-20=1350（米）。

三、畫圖法

畫圖法就是答題者通過分析題目，把題目中的信息用圖形（線段圖、實物圖等）畫出來，借助圖形進行分析，找出解決問題的方法。

例題4 在一次植樹活動中，彤彤所在的小組共有5 名學生，其他4 名學生植樹的棵數分別是6 棵、6 棵、7 棵、5 棵，彤彤植樹的棵數比5 名學生植樹棵數的平均數多4 棵。彤彤植樹的棵數是多少？

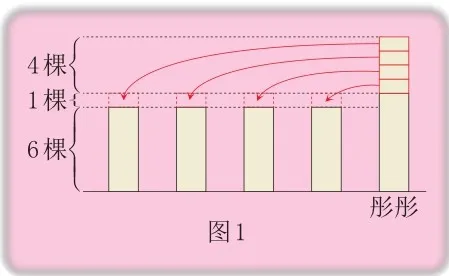
其他4名學生植樹棵數的平均數是（6+6+7+5）÷4=6（棵），把其他4名學生植樹的棵數都看作6棵，畫出圖形（如圖1），從圖1中可以看出，把彤彤比5名學生植樹棵數的平均數多出的4棵樹平均分給其他4名學生，每名學生能分到4÷4=1（棵），這樣，其他4名學生植樹的棵數都是6+1=7（棵），算出的7棵就是5名學生植樹棵數的平均數，彤彤植樹的棵數是7+4=11（棵）。

四、移多補少法

在計算一組數據的平均數時，可以用移多補少法，移多補少就是從數據中較大的數中拿出一部分補給較小的數，最后使得這組數據中每一個數都相同，這個相同的數就是這組數據的平均數。移多補少法是解答平均數問題的常用方法之一。

例題5 某地6 月份某一周7 天的最高氣溫分別是25℃、23℃、21℃、26℃、24℃、27℃、29℃，這一周的平均最高氣溫是多少？

先把這一周最高氣溫的數值按從大到小的順序排列，然后從較大的數中拿出一部分補給較小的數（如圖2），可知這一周的平均最高氣溫是25℃。

五、找中間數法

計算一組數據的平均數，可以先把這組數據按從小到大（或從大到小）的順序排列，排序后的數據滿足每相鄰兩個數的差都相同，當這組數據的個數是奇數個時，所求的平均數就是這組數據排序后最中間的那個數；當這組數據的個數是偶數個時，所求的平均數就是這組數據排序后最中間兩個數之和的一半。

例題6 在一次拔河比賽中，樂樂所在的隊伍共有5 名選手，他們的體重分別是41千克、45千克、44千克、42千克、43千克，這5 名選手的平均體重是多少？

把這5名選手的體重按從輕到重的順序排列：41，42，43，44，45。經過觀察可以發現，排序后每相鄰兩個數中，后面的數減去前面的數的差都是1，又已知這組數據的個數是奇數個，不需要計算，就可直接確定最中間的43是這組數據的平均數，所以，這5名選手的平均體重是43千克。

例題7 露露家今年上半年1 至6 月的電費支出分別是98元、95元、89元、92元、86元、83元。露露家今年上半年平均每個月的電費支出是多少？

將露露家的電費支出按從少到多的順序排列：83，86，89，92，95，98。經過觀察可以發現，排序后每相鄰的兩個數中，后面的數減去前面的數的差都是3，又已知這組數據的個數是偶數個，可知89與92之和的一半就是這組數據的平均數，所以露露家今年上半年平均每個月的電費支出是（89+92）÷2=90.5（元）。

六、假設法

在某些平均數問題中，給出的已知信息較少，不易求解，我們可以假設出某一信息，這樣便可順利解題了。

例題8 明明從家出發去爺爺家，去時的速度是15千米/ 時，返回時的速度是10千米/ 時。明明往返的平均速度是多少？

根據平均數問題的常規解法可知，要計算明明往返的平均速度，應知道他往返爺爺家的總路程和總時間，題中這兩個信息都沒有給出。我們不妨假設從明明家到爺爺家的路程是30千米（假設的30既是15的倍數，又是10的倍數，這樣假設是為了方便計算），則可算出他往返的總路程是30×2=60（千米）。明明去爺爺家用的時間是30÷15=2（時），返回家用的時間是30÷10=3（時），往返的總時間是2+3=5（時）。明明往返的平均速度是60÷5=12（千米/時）。

小朋友，你學會了嗎，在遇到解答平均數的問題時，一定要認真思考，選擇合理的方法解答。