小學數學統整型關鍵課的確立與實施

［摘要］ 實施關鍵課教學是落實新課標課程內容結構化這一變化的腳手架。關鍵課可供遷移、可供生長，有利于核心素養的培養；統整型關鍵課是復習課中的一種重要課型，有助于學生建立更深刻的知識體系，進一步凸顯知識本質。本文以六年級下冊總復習“圖形的測量”為例，通過憶“關鍵過程”、抓“關鍵圖形”、定“關鍵線段”，展現統整型關鍵課的確立與實施的思路及做法。

［關鍵詞］ 統整型；關鍵課；小學數學；“圖形的測量”

“課程內容結構化”是《義務教育數學課程標準（2022年版）》（以下簡稱“新課標”）的顯著變化之一，實施關鍵課教學是落實新課標這一變化的腳手架，因為關鍵課可供遷移、可供生長，有利于學生核心素養的培養。統整型關鍵課是復習課中的一種重要課型，有助于學生建立更深刻的知識體系，進一步凸顯知識本質，實現讀書“由厚到薄”。下面，以北師大版小學數學六年級下冊總復習“圖形的測量”為例，探討統整型關鍵課的確立與實施。

一、關鍵課的概念、類型及特征

認識統整型關鍵課，首先要了解其前概念“關鍵課”，即理解“關鍵課”的概念、類型和特征。

1.關鍵課的概念。俞正強老師將“種子課”界定為“關鍵課”，認為它是“處于學生思維發展重要節點的課，是老師教學應該花大力氣的課”。筆者認為，小學數學關鍵課是指以發展學生數學核心素養為目標，以學科大觀念中關鍵內容或關鍵節點為重點，對小學數學一個學習單元的認知起重要作用的一類課。例如，“什么是面積”是三年級下冊“面積”單元的關鍵課。首先，它是學生學習圖形測量的一個重要節點，因為學生之前學習了“長度測量”，包括“周長測量”，現在從一維測量跨越到二維測量，在數學知識和學生認知上都是一個飛躍；其次，“什么是面積”是“面積”單元的起始課，建立“面積”概念是學習面積單位和長方形面積公式的前提。因此，我們認為，關鍵課是源自數學知識或學生思維發展的起點、節點或拐點的一類課，其內容與方法是可遷移、可生長的。

2.關鍵課的類型。基于對關鍵課的本質內涵的理解，我們可以將其分為起點型、節點型和統整型_{LOjI4KqBxwvZNNg4J8RKjuTd/+9trbcYuBNvQ2ceXVQ=}等類型。起點型關鍵課是指源自數學知識起點的一類課，一般指某一學習單元中的第一課，其內容具有基礎性、根本性和生長性的特點，后幾課時的知識都是由它引發或展開的。例如，六年級下冊“圓柱和圓錐”單元中，“面的旋轉”是該單元的起始型關鍵課，因為這是從動態的視角認識立體圖形，掌握圓柱和圓錐的特點，為后續學習圓柱的表面積和體積以及圓錐的體積打下基礎。

節點型關鍵課是指處在數學知識或學生思維發展的重要節點的一類課。例如“長方形的面積”，它是學生在認識了長方形、知道了面積的概念和面積單位的基礎之上學習的，為后續學習多邊形面積、立體圖形的表面積打下基礎，是空間形式認識發展上的一次飛躍，是研究圖形面積的“節點型關鍵課”。

統整從字面上理解指統一、整合。統整型關鍵課是指學生經過一個階段學習后，教師引導學生將學過的數學知識進行整理、歸納和總結，使其形成一個有意義的整體的課。統整型關鍵課有助于學生建立更深刻的系統，讓學生觸及知識的本質。例如，筆者曾執教過的“加減乘除手拉手”就屬于統整型關鍵課。學生經過一、二年級的學習，對加減乘除法有了一定的認識，但是對四則運算的學習是分散的。因此，在學生學習完除法后，有必要設計一節“統整型關鍵課”，將“加減乘除”放在一起，通過分類活動，幫助學生溝通四則運算之間的聯系，促使他們掌握運算的本質。

3.關鍵課的特征。基于對關鍵課概念的理解和類型的探討，我們用一棵樹來做比方，起點型關鍵課是樹的根，是基礎，整棵樹要從根部汲取營養，因而起點型關鍵課具有基礎性和生長性的特征；節點型關鍵課是樹干與樹枝的聯結點，是整棵樹的關鍵點，可供遷移，因而節點型關鍵課具有深刻性、遷移性；統整型關鍵課可以看作一棵完整的樹，樹的各個部分相互關聯、相互作用，形成一個有機的整體，它強調關聯，關注本質，因而統整型關鍵課具有整體性、系統性的特征。

二、統整型關鍵課的確立分析

無論是在學習、研究還是工作中，統整都發揮著重要的作用，統整型關鍵課有助于學生建立更深刻的結構和對知識本質更深入的理解。作為總復習的關鍵課，自然屬于統整型關鍵課。該類課不僅具有關鍵課的一般特征，也體現了總復習的特點。對于一個主題的總復習，一般要經歷“理要點—找聯系—會應用”三個階段。“理要點”是復習單元的第一層面的教學單位，它是復習的起始課，通過回顧并梳理該復習單元的知識要點，形成對該單元的整體概覽；“找聯系”是復習單元的第二層面的教學單位，是復習的關鍵課，通過尋找復習單元知識間的聯系，進一步凸顯知識本質，實現“讀書由厚到薄”；“會應用”是復習單元的第三層面的教學單位，通過多層次、多維度的練習，促使知識得以固化、變化和深化，提高學生綜合運用知識解決實際問題的能力，發展應用意識。

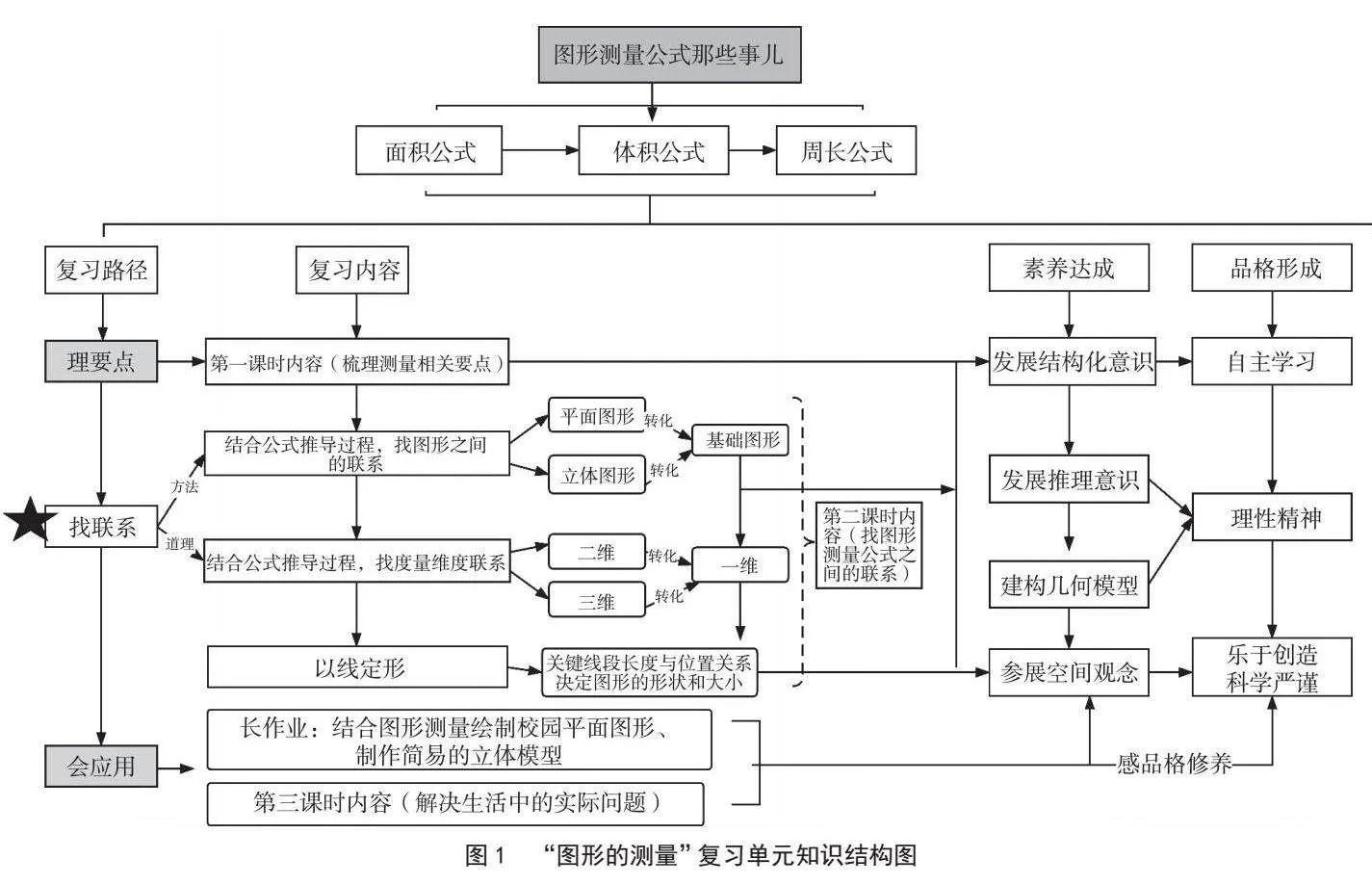
例如，“圖形測量公式那些事兒”就是“圖形的測量”復習單元的關鍵課，是在“理要點”的基礎上找圖形測量公式之間的聯系，旨在打通一維測量、二維測量和三維測量，凸顯圖形測量“度量單位的個數”這一本質，體會圖形測量的一致性。如圖1所示，“圖形測量公式那些事兒”作為“圖形的測量”復習單元的關鍵課，在“理要點”的基礎上引導學生找圖形測量公式之間的聯系，從一維測量轉向二維測量和三維測量，凸顯圖形測量“度量單位的個數”這一本質。具體內容如下：從找圖形面積公式聯系入手，結合公式的推導過程，找到圖形之間的聯系，即圓形、三角形、梯形、平行四邊形都可以轉化為長方形，并遷移運用，將其他不規則、較復雜的圖形轉化為學過的基本圖形，最終都轉化為長方形，從而確定長方形為面積測量的基礎圖形。結合長方形的面積公式推導過程，將二維測量轉化為一維測量，由數面積單位的個數到算面積，優化思維模型。立體圖形的體積公式之間的聯系與公式推導過程同樣如此，周長公式也是這樣，做到觸類旁通，由此培養學生的量感及空間觀念。

三、統整型關鍵課的實施案例

高質量的復習，需要設計高質量的統整型關鍵課，從而幫助學生既“見森林”又“建森林”。現以“圖形測量公式那些事兒”為例，展現統整型關鍵課的課堂教學實施策略。

（一）憶“關鍵過程”，找圖形測量公式的聯系

在小學階段，圖形測量公式包括周長公式、面積公式和體積公式。在總復習階段要想通過建立圖形測量公式之間的聯系找到度量本質，更宜從面積公式開始。因為小學階段圖形周長公式較少，而面積公式較多且比周長和體積更為繁雜，同時面積的內容比重也較大。以北師大版教材為例，周長和體積只需要分為兩個階段就學習完了，而面積則分為長方形、多邊形面積以及圓的面積三個階段來學習。復習課應先復習重點和學生易混淆的知識，稍微簡單的知識，學生可以舉一反三。基于此，筆者認為可以重點讓學生梳理面積公式推導過程，養成結構化的意識，幫助學生梳理面積知識，使之結構化。進而，讓學生借用梳理面積公式的方式和方法來梳理體積公式之間的聯系。最后，學生自然會聯想到周長公式，并可能做大膽猜測：周長公式的測量方法和其中的道理也是一回事。這樣一氣呵成，符合學生學習的一般規律。如何找到圖形測量公式之間的聯系？圖形測量公式的關鍵在于推導過程，因而筆者設計了回顧公式的推導過程，突出公式之間的聯系。

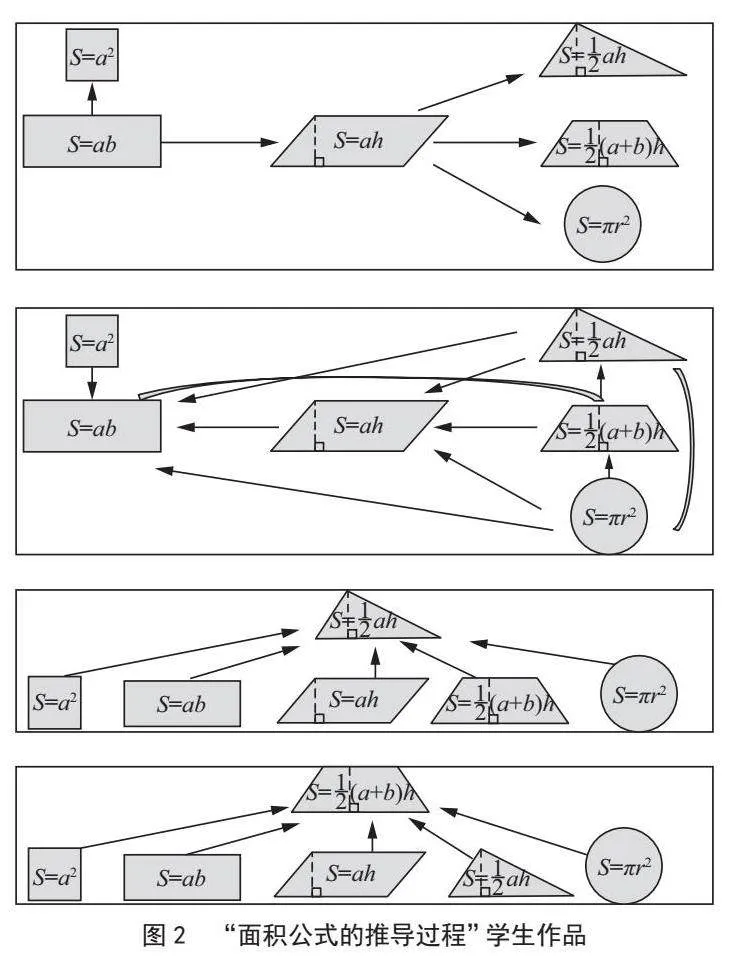
一是回顧面積公式的推導過程，找到面積公式之間的聯系。基于學科大概念，設計核心問題“面積公式之間有什么聯系”，布置“回顧面積公式的推導過程，找一找它們之間的聯系”這一學習任務，讓學生以四人小組為單位，用學具袋里的圖形在小黑板上擺一擺，并用箭頭連一連。如圖2所示，學生作品如下：①箭頭從長方形發出的，即從學習的先后順序找到聯系；②箭頭都指向長方形，利用轉化的方法推導公式，即新學圖形的面積都可以轉化為學過的圖形的面積；③箭頭指向三角形的，因為平面圖形的面積可以通過分割轉化成三角形來計算；④箭頭指向梯形，因為梯形面積公式是多邊形面積的萬能公式，圓的面積也可以轉化為梯形來計算。

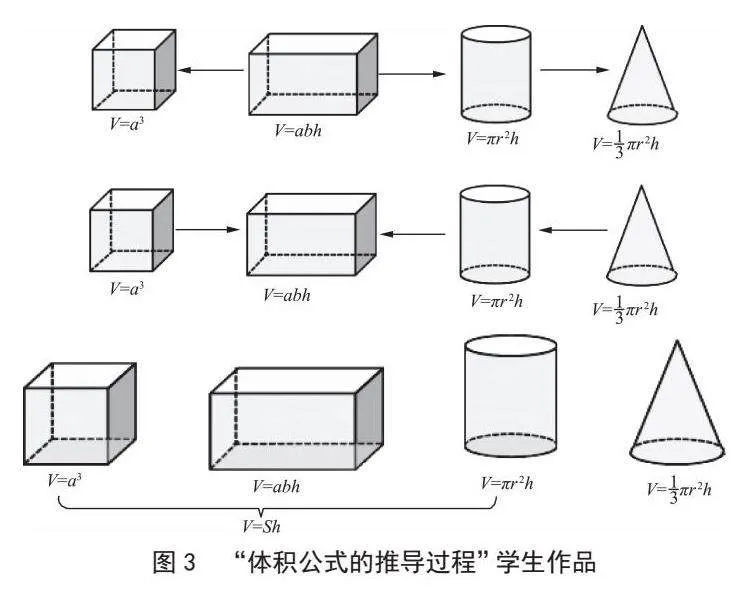
二是遷移“找聯系”的經驗，找到體積公式之間的聯系。在解決核心問題“體積公式的推導方法與道理也是一回事兒嗎”時，設計了“回顧立體圖形體積公式的推導過程，和同桌說一說它們的聯系”，學生通過交流匯報，呈現了如圖3的成果：①箭頭由長方體發出的，即從學習路徑上找到聯系；②箭頭都指向長方體的，因為正方體體積可以由長方體推導得到，圓柱可轉化為長方體，圓錐可轉化為等底等高的圓柱；③長方體、正方體、圓柱、圓錐的體積都與底面積、高有關。進而引入對點變式練習，明確“直柱體的體積=底面積×高”。

通過回顧圖形測量公式的推導過程，厘清圖形測量公式之間的關聯，將它們連成線、結成網，形成完整的“知識面”，促使學生體會轉化的數學思想方法，明白“面積公式在推導方法上是一回事兒”“體積公式在推導方法上也是一回事兒”，從而實現對知識形成過程的理解。

（二）抓“關鍵圖形”，明圖形測量知識的聯系

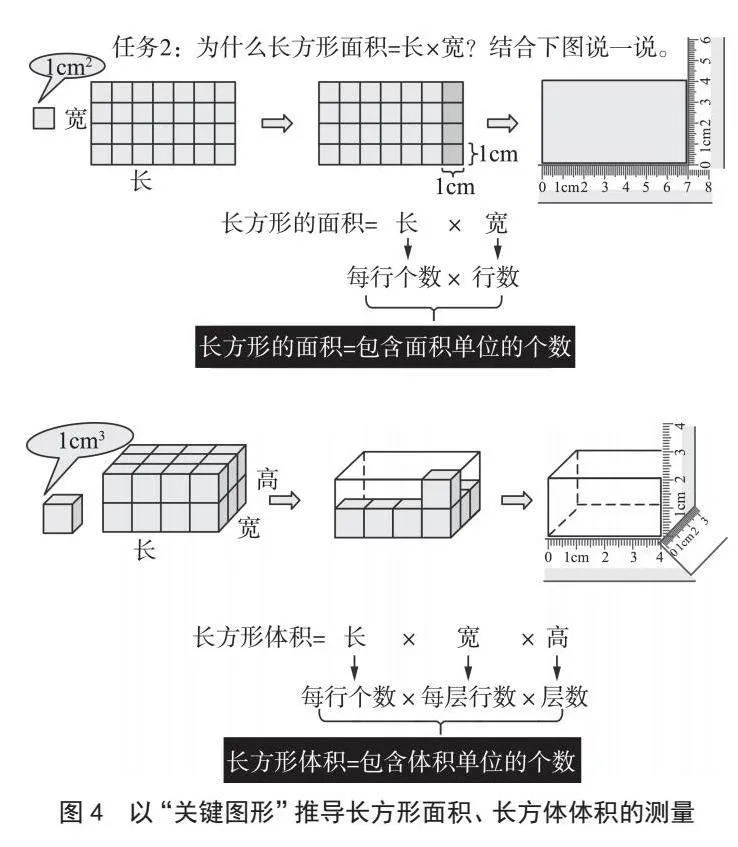
統整型關鍵課教學強調知識之間的關聯，這就需要抓住圖形測量的本質，回到知識的原點進行理解。通過找圖形測量公式之間的聯系，學生明白“長方形、長方體分別是圖形面積測量和體積測量的基礎”。于是，聚焦關鍵圖形“長方形”和“長方體”，讓學生結合長方形面積公式的推導過程、長方體的體積公式的推導過程，闡述“為什么長方形面積=長×寬”和“為什么長方體的體積=長×寬×高”的道理，啟發學生回到原點去理解“長方形的面積=包含面積單位的個數=每行面積單位個數×行數”和“長方體的體積=包含體積單位的個數=每行體積單位個數×行數×層數”（見圖4），進而發現量“面”和量“體”可轉化成量“線”再用公式算，都能得到圖形中包含面積單位或體積單位的個數，從而得出面積測量和體積測量的道理是一回事兒。

面積測量、體積測量存在維度的轉化，而周長測量屬于一維測量，并沒有維度的轉化，根據圖形的特征只需要測量關鍵線段的長度，再利用周長公式即可得到圖形的周長。進而，將找面積公式、體積公式之間的聯系的經驗遷移到周長公式上，讓學生觀看相關微課，打通一維測量、二維測量和三維測量之間的聯系，感悟圖形測量本質上的一致性。最后，將本課課題“圖形測量公式那些事兒”變更為“圖形測量公式一回事兒”。

（三）定“關鍵線段”，建圖形測量的本質模型

周長的本質是圖形一周中包含多少個長度單位，平面圖形面積的本質是平面圖形中包含多少個面積單位，立體圖形體積的本質是立體圖形中包含多少個體積單位。周長、面積、體積不僅在知識結構上有著內在的聯系，更重要的是它們在方法原理上有著共同的測量本質。因此，總復習時需要提供給學生合適的學習材料和不同情景，讓學生經歷分類和總結實踐，感受到在實際測量時，對不規則圖形的周長、面積或體積，常常可以先通過轉化再測量，對于規則圖形，可以根據圖形整體特征，只需要測量關鍵線段的長度，再運用公式算出其中包含的單位個數，從而建立圖形測量的本質模型。

基于此，給出下面兩個任務：通過給定的“關鍵線段”（有兩條相互垂直的線段，分別長15厘米和10厘米），①你能想到哪些平面圖形？請畫一畫；②算出你畫的圖形的面積。如圖5所示，學生在想象、操作中感受到二維面積計算可以轉化為一維長度的測量，再用公式算出其中包含的面積單位個數，圖形形狀雖然不同，但只要關鍵線段確定，圖形的面積就能確定，在分類、比較中領悟“關鍵線段的長短決定平面圖形的大小”，從而發展學生的空間觀念，建立起圖形面積測量的本質模型。

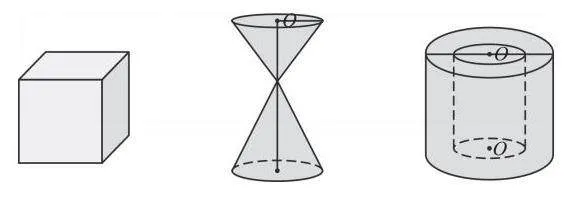
隨后，又出示立體圖形，設計如下的任務：至少量出幾條線段的長度就能計算出下圖中立體圖形的體積？畫一畫。

該任務中，學生會嘗試將上面總結的圖形面積測量的模型聯想、遷移到立體圖形中，發現立體圖形仍然是根據圖形的特征，找到關鍵線段，就可以算出包含的體積單位個數。通過以上兩個任務的設計，讓學生經歷圖形測量模型建構的過程，進一步加深對圖形的認識。

概言之，在“圖形的測量”的統整型關鍵課教學中，教師要緊扣圖形測量的本質，抓住圖形測量的關鍵要素，通過憶“關鍵過程”，找圖形測量公式的聯系；抓“關鍵圖形”，明圖形測量知識的聯系；定“關鍵線段”，建圖形測量的本質模型，真正實現讀書“由厚到薄”。關鍵課教學是一個系統工程，教師要從學科知識結構化的特點和學生認知規律出發，聚焦核心素養，立足單元整體教學對單元學習內容進行解讀，建構知識結構，設計單元課時，確定單元教學關鍵課，并規劃單元學習路徑，及時反思、調整、優化，以關鍵課的學習撬動整個單元內容的學習，促進學生對知識本質的把握、對思想方法的遷移運用、對單元學習內容的結構化認識，進而推動學生數學核心素養的發展。

［參考文獻］

［1］崔允漷.素養本位的單元設計，助力各國進入“素養時代”[J].上海教育，2021（32）：22-25.

［2］鄧穎潔，宋顯慶.聚焦關鍵課例 發展關鍵能力[J].江西教育，2022（27）：31-34.

［3］夸美紐斯.大教學論·教學法解析[M].北京：人民教育出版社，2006：147.

［4］陸蘭芳.初三數學復習課的有效教學模式[J].生活教育，2012（22）：52-53.

黃慧章 四川省成都市龍泉驛區第二小學校副校長，正高級教師，四川省特級教師，教育部“國培計劃”指導專家。

蘭 云 四川省成都市龍泉驛區第二小學校，成都市骨干教師。

徐龍燕 四川省成都市龍泉驛區第二小學校。