課本中一道求面積最小值問題的解法探究及變式

眾所周知，高考試題一般在教科書上都可以找到“影子”。“源于教材，高于教材”已經(jīng)成為高考命題的一條重要原則，也是專家青睞的一種命題手法。這就啟示我們要研究課本習(xí)題，重視課本習(xí)題的組合、演變、延伸、推廣及拓展。下面以課本中的一道復(fù)習(xí)參考題為例，分析題目的背景、結(jié)構(gòu)和考查目標(biāo)，從不同視角探究題目的解法，然后對題目進行變式拓展，希望對同學(xué)們的學(xué)習(xí)有所幫助。

一、題目呈現(xiàn)

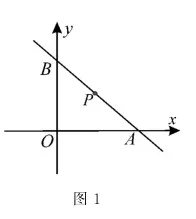
題目 如圖1，過點P（ 1， 1）作直線A B，分別與x軸的正半軸， y軸的正半軸交于點A， B。當(dāng)直線A B在什么位置時，△A O B的面積最小？最小面積是多少？

此題是人教A版《數(shù)學(xué)選擇性必修第二冊》第五章“一元函數(shù)的導(dǎo)數(shù)及其應(yīng)用”中復(fù)習(xí)參考題5的第1 0題。

題目是一道典型的求函數(shù)最值問題，由于解答入口較寬，求函數(shù)最值除用導(dǎo)數(shù)方法外，還可以運用基本不等式、一元二次方程判別式、對勾函數(shù)、凹凸函數(shù)等知識點，利用整體思想、函數(shù)思想、消元思想等數(shù)學(xué)思想，主要的解題方法有基本不等式法、判別式法、導(dǎo)函數(shù)法等。下面避開導(dǎo)數(shù)，利用所學(xué)方法進行解答，以饗讀者。

二、解法探究

點評：解法1、解法2是解題的常規(guī)思路，也是直接利用基本不等式進行求最值。當(dāng)然，本題可以從多角度建立直線方程或?qū)で驛， B兩點的坐標(biāo)關(guān)系，如可以利用三點共線、斜率相等、向量共線等，請同學(xué)們自行解答。

故當(dāng)直線A B的橫截距為2時，△A O B的面積最小，最小值是2。

點評：構(gòu)造法是一種創(chuàng)造性解題方法，它是一種解題的輔助手段，通過構(gòu)造適當(dāng)?shù)臄?shù)學(xué)對象（如圖形、模型、函數(shù)、方程、不等式、數(shù)列等）轉(zhuǎn)換命題，為解題創(chuàng)造條件。構(gòu)造法的核心是“構(gòu)造”，就是“創(chuàng)造適當(dāng)?shù)慕Y(jié)構(gòu)”，構(gòu)造法解題貴在“創(chuàng)新”。

點評：三角函數(shù)是一個非常精細、有用的工具，三角代換是構(gòu)造法的一種重要形式，其本質(zhì)體現(xiàn)了換元思想，消元策略，尤其利用三角函數(shù)的有界性可以求解其最值（值域）。

三、變式

在解完一道經(jīng)典習(xí)題后，可以通過改變問題的條件、結(jié)論以及問題的背景等進行變式，以鍛煉同學(xué)們靈活應(yīng)用不同方法解答問題的能力，達到做一題通一類，以不變應(yīng)萬變的運算素養(yǎng)。

變式3 過點P（ 2， 1）作直線l分別交x軸， y軸的正半軸于A， B兩點。

（ 1）求| O A |·| O B |的最小值，及此時直線l的截距式方程；

（ 2）求| P A |·| P B |的最小值，及此時直線l的截距式方程。

四、反思

同學(xué)們在平時學(xué)習(xí)中，要領(lǐng)悟教材主編的意圖，深入研究教材中的例題、習(xí)題。教材是連接課程方案與教學(xué)實踐的樞紐，是教師教與學(xué)生學(xué)的載體。教材例習(xí)題只是提供了基本的教學(xué)素材，并非教學(xué)內(nèi)容的全部，要樹立“用好教材，超出教材”的理念。研究教材時既要尊重教材，又要不拘泥于教材。我們只有吃透教材的精神與實質(zhì)，創(chuàng)造性地使用教材資源，才能不斷提高教材例題、習(xí)題的“附加值”。

（責(zé)任編輯 徐利杰）