旋轉角問題的深入探究


摘要:旋轉角問題對學生空間想象力和幾何思維的培養有著重要意義,然而,由于旋轉角問題的抽象性和復雜性,許多學生在解題過程中感到困惑.因此,研究初中旋轉角問題的教學策略,對于提高學生的數學能力和興趣具有重要意義.
關鍵詞:初中數學;旋轉角;教學策略;解題能力
旋轉角問題是初中數學中重要的幾何題型之一,本文探討了初中階段旋轉角問題的教學策略,通過分析旋轉角問題的特點,結合教學實踐,提出了針對性的教學方法和策略,旨在幫助學生更好地理解和掌握旋轉角知識,提高解題能力.
1旋轉角問題梳理
在線段上某一特殊點C處作固定大小的角∠DCE(如圖1、圖2),我們把與這個角有關的各種問題稱之旋轉角問題.
解決此類問題有以下四種常見方法.
(1)造等角.
以C為頂點再構造一個和∠DCE相等的角,這樣就可以得到一對新的相等的角,然后利用新角相等去解決問題.
(2)構造一線三角.
過旋轉角的頂點會有一些特殊的直線,利用這些直線構造一線三角.
(3)構造特殊三角形.
利用固定的旋轉角構造直角三角形或者等腰三角形等特殊三角形,以此來轉化成其他角的問題或者其他基本圖形問題.
(4)導出角的特殊關系.利用旋轉角的特殊關系進行分析、轉化,得到三角形中的特殊關系去解決問題.
總結:教學策略的實施有效提高了學生的旋轉角問題解題能力,通過直觀演示和動手操作,學生更容易理解旋轉角的概念和性質.
教師可以利用教具或多媒體展示旋轉過程,讓學生觀察旋轉前后圖形的變化,從而加深對旋轉角的理解.
2例題精講
例題如圖所示,在矩形ABCD中,AB=6,點E在邊BC上,∠CAE=45°,CE=10,則線段AE的長度為.
方法1:造等角(1).
把∠CAE看成是旋轉角,以A為頂點再造一個45°角和原45°角旋轉.
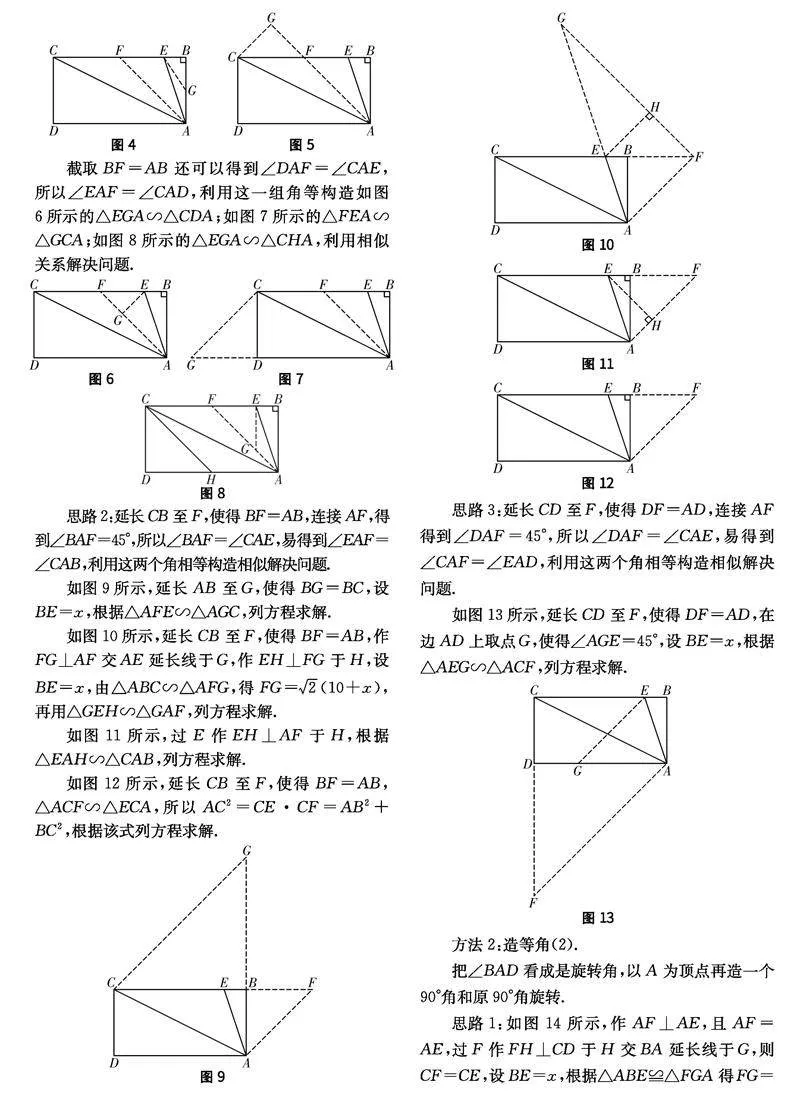
思路1:在邊BC上取點F,使得BF=AB,連接AF得到∠BAF=45°,所以∠BAF=∠CAE,易得到∠BAE =∠CAF,利用這兩個角相等構造相似解決問題.
如圖3所示,延長AB至H,使得BH=BE,延長AF交DC延長線于G,設BE=x,根據△AHE∽△AGC,列方程求解.
利用∠BAE=∠CAF相等,還可以構造如圖4所示的△ACF∽△AEG;如圖5所示的△ACG∽△AEB,列方程求解.
截取BF=AB
還可以得到∠DAF=∠CAE,所以∠EAF=∠CAD,利用這一組角等構造如圖6所示的△EGA∽△CDA;如圖7所示的△FEA∽△GCA;如圖8所示的△EGA∽△CHA,利用相似關系解決問題.
思路2:延長CB至F,使得BF=AB,連接AF,得到∠BAF=45°,所以∠BAF=∠CAE,易得到∠EAF= ∠CAB,利用這兩個角相等構造相似解決問題.
如圖9所示,延長AB至G,使得BG=BC,設BE=x,根據△AFE∽△AGC,列方程求解.
如圖10所示,延長CB至F,使得BF=AB,作FG⊥AF交AE延長線于G,作EH⊥FG于H,設BE=x,由△ABC∽△AFG,得FG=2(10+x),再用△GEH∽△GAF,列方程求解.
如圖11所示,過E作EH⊥AF于H,根據△EAH∽△CAB,列方程求解.
如圖12所示,延長CB至F,使得BF=AB,△ACF∽△ECA,所以AC2=CE·CF=AB2+BC2,
根據該式列方程求解.
思路3:延長CD至F,使得DF=AD,連接AF得到∠DAF=45°,所以∠DAF=∠CAE,易得到∠CAF=∠EAD,利用這兩個角相等構造相似解決問題.
如圖13所示,延長CD至F,使得DF=AD,在邊AD上取點G,使得∠AGE=45°,設BE=x,根據△AEG∽△ACF,列方程求解.
方法2:造等角(2).
把∠BAD看成是旋轉角,以A為頂點再造一個90°角和原90°角旋轉.
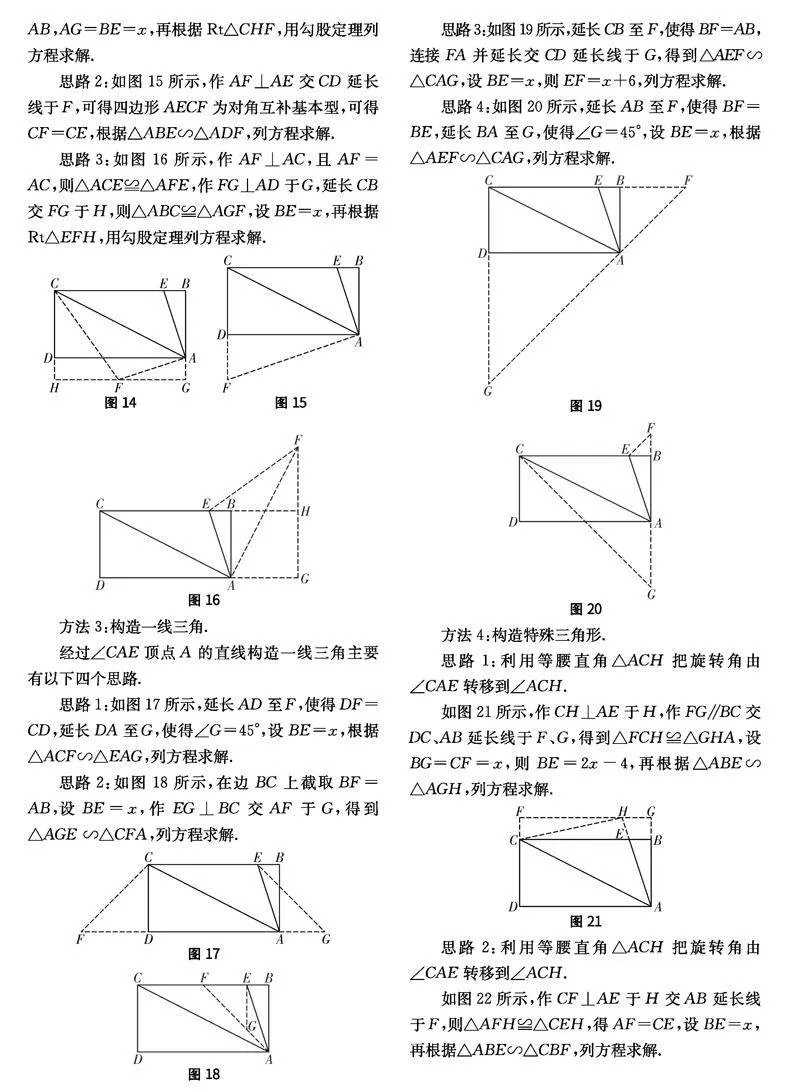
思路1:如圖14所示,作AF⊥AE,且AF=AE,過F作FH⊥CD于H交BA延長線于G,則CF=CE,設BE=x,根據△ABE≌△FGA得FG=AB,AG=BE=x,再根據Rt△CHF,用勾股定理列方程求解.
思路2:如圖15所示,作AF⊥AE交CD延長線于F,可得四邊形AECF為對角互補基本型,可得CF=CE,根據△ABE∽△ADF,列方程求解.
思路3:如圖16所示,作AF⊥AC,且AF=AC,則△ACE≌△AFE,作FG⊥AD于G,延長CB交FG于H,則△ABC≌△AGF,設BE=x,再根據Rt△EFH,用勾股定理列方程求解.
方法3:構造一線三角.
經過∠CAE頂點A的直線構造一線三角主要有以下四個思路.
思路1:如圖17所示,延長AD至F,使得DF=CD,延長DA至G,使得∠G=45°,設BE=x,根據△ACF∽△EAG,列方程求解.
思路2:如圖18所示,在邊BC上截取BF=AB,設BE=x,作EG⊥BC交AF于G,得到△AGE ∽△CFA,列方程求解.
思路3:如圖19所示,延長CB至F,使得BF=AB,連接FA并延長交CD延長線于G,得到△AEF∽△CAG,設BE=x,則EF=x+6,列方程求解.
思路4:如圖20所示,延長AB至F,使得BF=BE,延長BA至G,使得∠G=45°,設BE=x,根據△AEF∽△CAG,列方程求解.
方法4:構造特殊三角形.
思路1:利用等腰直角△ACH把旋轉角由∠CAE轉移到∠ACH.
如圖21所示,作CH⊥AE于H,作FG∥BC交DC、AB延長線于F、G,得到△FCH≌△GHA,
設BG=CF=x,則BE=2x-4,再根據△ABE∽△AGH,列方程求解.
思路2:利用等腰直角△ACH把旋轉角由∠CAE轉移到∠ACH.
如圖22所示,作CF⊥AE于H交AB延長線于F,則△AFH≌△CEH,得AF=CE,設BE=x,再根據△ABE∽△CBF,列方程求解.
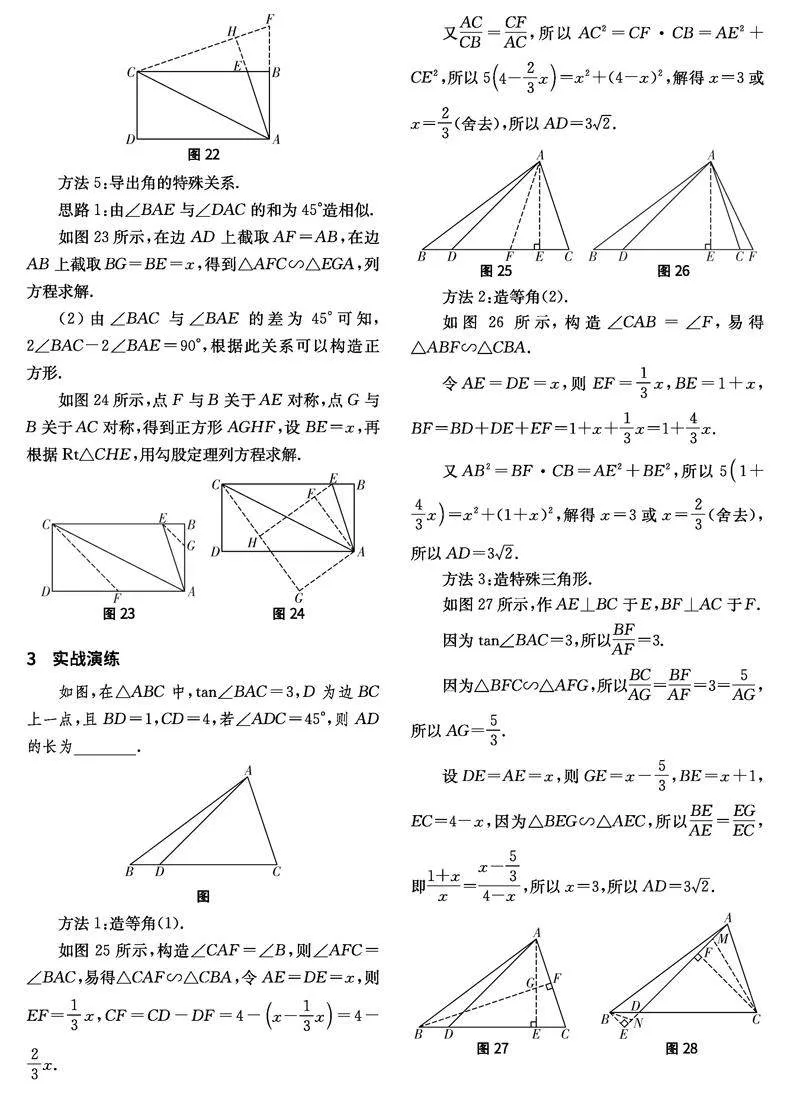
方法5:導出角的特殊關系.
思路1:由∠BAE與∠DAC的和為45°造相似.
如圖23所示,在邊AD上截取AF=AB,在邊AB上截取BG=BE=x,得到△AFC∽△EGA,列方程求解.
(2)由∠BAC與∠BAE的差為45°
可知,2∠BAC-2∠BAE=90°,根據此關系可以構造正方形.
如圖24所示,點F與B關于AE對稱,點G與B關于AC對稱,得到正方形AGHF,設BE=x,再根據Rt△CHE,用勾股定理列方程求解.
3實戰演練
如圖,在△ABC中,tan∠BAC=3,D為邊BC上一點,且BD=1,CD=4,若∠ADC=45°,則AD的長為.
方法1:造等角(1).
如圖25所示,構造∠CAF=∠B,則∠AFC=∠BAC,
易得△CAF∽△CBA,令AE=DE=x,則EF=13x,CF=CD-DF=4-x-13x=4-23x.
又ACCB=CFAC,所以AC2=CF·CB=AE2+CE2,所以54-23x=x2+(4-x)2,解得x=3或x=23(舍去),所以AD=32.
方法2:造等角(2).
如圖26所示,構造∠CAB=∠F,易得△ABF∽△CBA.
令AE=DE=x,則EF=13x,BE=1+x,
BF=BD+DE+EF=1+x+13x=1+43x.
又AB2=BF·CB=AE2+BE2,所以51+43x=x2+(1+x)2,解得x=3或x=23(舍去),所以AD=32.
方法3:造特殊三角形.
如圖27所示,作AE⊥BC于E,BF⊥AC于F.
因為tan∠BAC=3,所以BFAF=3.
因為△BFC∽△AFG,所以BCAG=BFAF=3=5AG,所以AG=53.
設DE=AE=x,則GE=x-53,BE=x+1,EC=4-x,
因為△BEG∽△AEC,所以BEAE=EGEC,即1+xx=x-534-x,所以x=3,所以AD=32.
方法4:造一線三等角.
如圖28所示,作CF⊥AD,BE⊥AD,垂足分別為F,E.
因為∠ADC=45°,DC=4,BD=1,
所以CF=22,BE=22.
構造∠BNE=∠CAB=∠DMC,所以BN=53,CM=453,
則△BNA∽△AMC,BN·MC=AM·NA.
設AD=x,
則33·433=x-23x-823,解得x=32.
4結語
傳統數學教學中,教師往往注重知識的灌輸和解題方法的傳授,導致學生缺乏獨立思考和創新能力,一題多解的教學策略強調從多個角度、多種方法解決問題,有助于提高學生的數學思維能力.[1]構建數學有效課堂是提高數學教學效果,培養學生數學思維能力的重要途徑,教師應從優化教學內容,改進教學方法,提高學生學習興趣等方面入手,不斷探索和實踐有效的數學教學方法和策略.
參考文獻
[1]中華人民共和國教育部.義務教育數學課程標準(2022年版)[M].北京:北京師范大學出版社,2022.

