非線性分布參數切換系統事件觸發采樣迭代學習控制

摘 要：本文研究了一類非線性分布參數切換系統事件觸發采樣迭代學習控制問題。基于系統的輸入和系統的輸出數據采樣，利用Lyapunov函數的方法得出事件觸發條件，使得控制器只在事件觸發條件被滿足時才更新，有效地減少了迭代學習過程中控制器的更新。通過嚴格的數學推導證明了事件觸發采樣迭代學習控制的收斂性。最后，通過數值仿真實驗驗證了算法的有效性。

關鍵詞：分布參數切換系統；數據采樣；迭代學習控制；事件觸發

中圖分類號：TP273 DOI：10.16375/j.cnki.cn45-1395/t.2024.04.008

0 引言

切換系統由子系統和子系統之間的切換規律組成，其作為一類典型的特殊混雜系統，被廣泛應用于電力系統[1]、交通控制系統[2]、化學過程[3]中。采樣控制是一種基于離散信號的控制策略，控制器會在固定的周期上獲取系統的信息，并通過采樣得到的數據對系統進行控制。關于切換系統采樣控制的研究，目前已在自適應控制[4]、T-S模糊系統[5]、Markovian切換[6]等相關研究上取得了一些成果。文獻[7]研究了具有異步現象的連續時間切換T-S模糊系統的量化采樣數據控制問題。文獻[8]研究了二階非線性系統異構多智能體切換系統的采樣數據一致性問題。類似于集中參數系統，分布參數系統的采樣控制也得到了學者們的廣泛關注，最早可追溯至1988年[9]。目前，隨著數字控制技術的發展，分布參數系統的采樣控制已成為研究熱點，在指數穩定[10]、魯棒控制[11]、模糊控制[12]、分布參數時滯系統[13]、非線性拋物型分布參數系統[14]等方面都有相應的研究成果。

迭代學習控制是一種具有廣泛應用前景的智能控制方法，其以優異的跟蹤控制性能有效地應對重復性和周期性的控制任務；同時由于其在工業領域的重要價值和應用潛力，迭代學習控制已成為一個備受關注的研究領域。文獻[15]研究了一類具有高相對度的非正則離散拋物型分布參數系統的迭代學習控制問題。相比于傳統的迭代學習控制，采樣迭代學習控制更加符合實際工業數字控制的要求。文獻[16]研究了一種具有不確定性的非線性連續系統，并提出了一種采樣迭代學習控制器。文獻[17]針對非線性系統提出了一種任意相對度的采樣迭代學習控制，該學習算法不需要對跟蹤誤差進行任何階次的數值微分。文獻[18]研究了時滯非線性系統的采樣迭代學習問題，當不存在初值誤差和不確定擾動時，算法可以使其在采樣點實現完全跟蹤。文獻[19]研究了具有局部Lipschitz連續的非線性非仿射系統的數據采樣迭代學習控制問題。根據現有的切換系統采樣控制研究，尚未發現針對分布參數切換系統采樣的研究。因此，對本文所涉及的切換系統進行采樣迭代學習控制研究具有重要意義。

事件觸發控制較早可以追溯到2002年，在文獻[20]中作者將其稱為Lebesgue采樣控制，并對比線性隨機系統在時間觸發和事件觸發2種機制作用下的不同，得出了事件觸發機制具有更好性能的結論。文獻[21] 針對帶有輸入限制的多智能體系統中存在通信帶寬限制的問題，提出了基于編碼-解碼器量化器的事件觸發條件，有效降低了控制器的更新頻率，節約了系統資源的消耗。近十年，學者們為了節約在迭代學習控制過程中控制器的資源利用問題，將事件觸發機制應用到迭代學習控制的研究當中。在關于事件觸發迭代學習控制問題的研究中，事件觸發條件設計的合理性是整個研究過程的核心問題，也是學者最關心的問題之一。文獻[22-23]采用了一種Lyapunov函數的方法推導出事件觸發條件。文獻[24-25]通過2D系統建模的方法對事件觸發迭代學習控制的收斂性進行了分析。事件觸發迭代學習控制能夠有效地解決復雜系統的跟蹤控制問題，在多智能體方面，學者們對其進行了大量的研究，目前已在帶有量化器的多智能體系統[26]、非同階分數階多智能體系統[27]、固定有向圖下的無模型多智能體系統[28]、非仿射非線性離散時間多智能體系統[29-30]、具有切換拓撲的異構網絡多智能體系統[31]、數據丟包的多智能體系統[32]、多地鐵列車系統[33]等取得了相關的成果。文獻[34]進一步分析了局部Lipschitz非線性多智能體系統的魯棒跟蹤問題，提出了一種基于觀測器的分布式事件觸發迭代學習控制框架。

本文針對非線性分布參數切換系統，提出了事件觸發采樣迭代學習控制方法。根據Lyapunov函數的方法得出事件觸發條件，在每次迭代過程中依據事件觸發條件的判斷情況進行更新學習。通過足夠次數的迭代后，可以使得系統輸出在采樣時刻上達到完全跟蹤。采用本文對控制器的設計方法，控制器的更新頻率低于傳統迭代學習，能有效地節約資源。

本文中，[Rn]和[Rn×m]分別表示[n]維Euclidean空間和[n×m]維實數矩陣空間。對于[n]維向量[c=（c1，c2，…，cn）]，其范數的定義為[‖c‖=l=1nc2l]。對于[n×m]維矩陣[A]，其范數的定義為[‖A‖=λmax（ATA）]，其中[λmax（?）]是矩陣最大特征值。[L2（Ω）]是定義在有界開子集[Ω]上的平方可積函數組成的Banach空間。對于[ω（x）∈L2（Ω）?Rn]，其[L2]范數的定義為[‖ω‖L2=（ΩωT（x）ω（x）dx）12]。對于[f（x，s）：Ω×N→Rn]，[f（?，s）∈L2（Ω）?Rn]，[s∈N]，[N]為自然數，其[（L2， λ）]范數的定義為[‖f‖（L2， λ）=sups∈[0，n]{a-λs‖f（?，sh）‖2L2}]，其中[a>1]，[λ>0]，h為采樣時間，是一個固定的常數。

1 問題描述

考慮如下重復運行在[[0，T]]上的分布參數切換系統

[?Qk（x，t）?t=ΔQk（x，t）+fα（t）（t，Qk（x，t），uk（x，t）），yk（x，t）=gα（t）（t，Qk（x，t））+Gα（t）（t）uk（x，t），]

（1）

式中：[Qk∈Rn]是系統狀態向量，其中[k]是迭代批次；[x]是空間變量，[t]是時間變量，[（x，t）∈Ω×[0，T]]，[Ω∈Rq]是帶有光滑邊界的有界開子集；[Δ]是定義在[Ω]上的Laplace算子，即[Δ=z=1q?2/?x2z]；[fα（t）]，[gα（t）]是一系列非線性函數；[uk∈Rm]是控制輸入向量；[yk∈Rw]是系統輸出向量；[Gα（t）（t）]是具有合適維數的矩陣；[α（t）]是切換規則，[α（t）：[0，T]→M=[1，2，… ，m]]。

假設1 對于上述系統，其第一個子系統的初始狀態和期望的初始狀態相同，邊界條件為Dirichlet邊界條件，即[Q（0，t）=Q（l，t）=0]，[l>0]。

假設2 對于給定的期望軌線[yd（x，t）]，存在唯一的期望輸入[ud（x，t）]和期望狀態[Qd（x，t）]。

假設3 任意一個子系統只激活1次，子系統的切換規則：

[α（t）=i=1， 0≤t<t1，2， t1≤t<t2， …m， tm-1≤t≤T.] （2）

假設4 [fi，gi ： L2（Ω）→L2（Ω）?Rn]，存在常數[Lfi、Lgi>0]，[i=1，2，… ，m]，使得

[‖fi（t，Q1，u1） -fi（t，Q2，u2）‖= ][Lfi（‖Q1-Q2‖+‖u1-u2‖），] （3）

[‖gi（t，Q1）-gi（t，Q2）‖=Lgi‖Q1-Q2‖.] [（4）]

本文將采樣控制器應用于非線性分布參數切換系統中。在每一個被激活的切換子系統中采樣[ni+1]次，采用符號[ts，i]表示采樣時刻，其中[i]表示被激活的子系統，[s]表示在被激活的子系統[i]中的采樣時刻，[s∈{0，1，… ，ni}]。在任意2個相鄰的采樣時刻之間的采樣區間是一個固定的常數[h]，這意味著系統的控制輸入表示為[uk（x，t）=uk（x，ts，i）]，[t∈（ts，i，ts，i+h）]。為了確保在每一個被激活的子系統中至少存在一個采樣時刻，切換子系統的最小運行時間[τd]應大于采樣區間常數[h]。本文提出的事件觸發采樣迭代學習控制的控制目標是在非線性分布參數切換系統的采樣時刻實現完全跟蹤。

2 主要結論

2.1 事件觸發條件

首先，定義事件觸發誤差為[δek（x，ts，i），]有[δek（x，ts，i）=][ekl-1（x，ts，i）-ek（x，ts，i）]，其中[ekl-1（x，ts，i）=ykl-1（x，ts，i）-yd（x，ts，i）]，[ek（x，ts，i）=] [yk（x，ts，i）-] [yd（x，ts，i）]。[ts，i]時刻的觸發誤差是該時刻上一次事件觸發的輸出誤差與該時刻第[k]次迭代的輸出誤差之間的差值，[k>kl-1]。根據Lyapunov函數的原理，沿迭代方向上建立一個正定的函數[V（k，ts，i）=‖ek（?，ts，i）‖2L2]。

[ΔV（k，ts，i）=V（k，ts，i）-V（k-1，ts，i）= ‖ek（?，ts，i）‖2L2-‖ek-1（?，ts，i）‖2L2= ‖ekl-1（?，ts，i）-eet，k（?，ts，i）‖2L2-‖ek-1（?，ts，i）‖2L2.（5）]

注1 其中的事件觸發誤差為第[k]次的事件觸發誤差。須經過事件觸發條AuHwAKVpOJU2TqYNFmsMyw==件的判斷才能確定第[k]次是否為[kl]。因此，第[k]次的系統輸入應該保持與[kl-1]一致，即[δek（x，ts，i）=gi（ts，i，Qkl-1（x，ts，i））-gi（ts，i，Qk（x，ts，i））]。

當[ΔV（k，ts，i）<0]，則可以在控制輸入不變的情況下保證系統收斂；當[ΔV（k，ts，i）≥0]，則當前的控制輸入不能保證系統收斂，需要對控制器進行更新。在此基礎上引入一個可調節的事件觸發參數[β]，得到本文的事件觸發為

[kl=inf{k>kl-1‖ekl-1（?，ts，i）-eet，k（?，ts，i）‖2L2- β‖ek-1（?，ts，i）‖2L2≥0}.] （6）

注2 事件觸發參數[β∈[0，1]]，其能夠有效地改變事件觸發機制的松弛度。當事件觸發參數[β=0]時，事件觸發機制將失去其篩選數據的效果。

2.2 控制器設計和收斂性分析

帶有零階保持器的開環事件觸發采樣迭代學習控制器設計如下，

[uk（x，t）=ukl-1（x，ts，i）+Γekl-1（x，ts，i）， k=kl，ukl-1（x，ts，i）， k∈（kl-1，kl），] （7）

式中：[t∈[ts，i，ts，i+h）]；[Γ]是開環迭代學習控制增益。

注3 在采樣時刻上，當滿足事件觸發條件（6）時，該控制器會進行更新；當不滿足事件觸發條件（6）時，該控制器保持上一次迭代學習控制的輸入。在采樣區間上，通過零階保持器對控制輸入進行保持。

定理1 對于滿足假設1—假設3的分布參數切換系統，在開環事件觸發迭代學習控制（7）以及事件觸發條件（6）的作用下，若下面不等式成立：

[2λGiΓ<1， i=1， 2 ，… ， m][，]

其中[λGiΓ=maxn∈[0，ni]λmax（（I+Gi（nh）Γ）T（I+Gi（nh）Γ））]，則系統在[k→∞]時，[‖ek（?，ts，i）‖2L2]收斂到0。

證明 根據事件觸發和非事件觸發這2種情況來證明事件觸發采樣迭代學習控制的收斂性。

步驟1 考慮事件觸發的情況，即[k=kl]。

1）當第一個子系統被激活時，[t∈[0，t1）]。

在采樣區間[[（n-1）h，nh]]上有

[??tQkl（x，t）=ΔQkl（x，t）+（f1（t，Qkl（x，t），ukl（x，t））-]

[f1（t，Qkl-1（x，t），ukl-1（x，t）））.] （8）

對式（8）兩邊同時乘[Qkl（x，t）]，可以得到

[12??t（QTkl（x，t）Qkl（x，t））=QTkl（x，t）ΔQkl（x，t）+]

[QTkl（x，t）（f1（t，Qkl（x，t），ukl（x，t））- f1（t，Qkl-1（x，t），ukl-1（x，t）），] fsJZ3ChLlfiiUtAhWSZQZg== （9）

式中：[Qkl（x，t）=Qkl（x，t）-Qkl-1（x，t）]。

將式（9）兩邊對[x]進行積分，根據[L2]范數的定義，得到

[ddt（‖Qki（?，t）‖2L2）=2ΩQTkl（x，t）ΔQkl（x，t）dx+][2ΩQTkl（x，t）（f1（t，Qkl（x，t），ukl（x，t））-]

[f1（t，Qkl-1（x，t），ukl-1（x，t））]<C：＼Users＼PC64＼Desktop＼2wzr廣西科技大學學報第4期＼Image＼W方括號.eps> [dx≤2QTkl（x，t）?Qkl（x，t）|x∈?Ω-]

[2ΩQTkl（x，t）?Qkl（x，t）dx+（Lf1+1）‖Qkl（?，t）‖2L2+]

[Lf1‖ukl（?，t）‖2L2，] （10）

式中：[ukl（x，t）=ukl（x，t）-ukl-bL3tatZWRC6NC92DsVJtrg==1（x，t）]。

對不等式（10）兩邊關于[t]進行積分，并使用Bellman-Gronwall不等式，得到

[ ‖Qkl（?，nh）‖2L2 ≤‖Qkl（?，（n-1）h）‖2L2+（n-1）hnh（ξ‖Qkl（?，τ）‖2L2+ ζ‖ukl（?，τ）‖2L2）dτ ≤exp（ξnh）‖Qkl（?，（n-1）h）‖2L2+（n-1）hnhexpξ（nh-τ）ζ‖ukl（?，τ）‖2L2dτ ≤exp（ξT）‖Qkl（?，（n-1）h）‖2L2+ζ‖ukl（?，（n-1）h）‖2L2（n-1）hnhexpξ（nh-τ）dτ =κ‖Qkl（?，（n-1）h）‖2L2+φ‖ukl（?，（n-1）h）‖2L2 ≤κn‖Qkl（?，t0，1）‖2L2+φj=0n-1κn-1-j‖ukl（?， jh）‖2L2， （11）]式中：[ξ=maxi∈MLfi+1]，[ζ=maxi∈MLfi]，[κ=exp（ξT）]，[φ=ζ（（exp（ξh）-1）/ξ）]。

在采樣時刻[nh]上有

[ukl（x，nh）-ukl-1（x，nh）=Γekl-1（x，nh），] （12）

[ekl（x，nh）=ekl-1（x，nh）+ykl（x，nh）-ykl-1（x，nh）=]

[（g1（nh，Qkl（x，nh））-g1（nh，Qkl-1（x，nh）））+ekl-1（x，nh），]

（13）

其中[ekl-1（x，nh）=（I+G1（nh）Γ）ekl-1（x，nh）]。

依據式（12）、式（13）可以得到

[uTkl（x，nh）ukl（x，nh）≤λΓeTkl-1（x，nh）ekl-1（x，nh），] （14）

[eTkl（x，nh）ekl（x，nh）≤2λG1ΓeTkl-1（x，nh）ekl-1（x，nh）+]

[ 2（g1（nh，Qkl（x，nh））-g1（nh，Qkl-1（x，nh）））T× （g1（nh，Qkl（x，nh））-g1（nh，Qkl-1（x，nh）））， （15）]

其中[λΓ=λmax（ΓTΓ）] ，[λG1Γ=maxn∈[0，n1]λmax（I+G1（nh）Γ）T×]

[（I+G1（nh）Γ）]。

將式（14）、式（15）兩邊對[x]進行積分，根據[L2]范數的定義，得到

[‖ukl（?，nh）-ukl-1（?，nh）‖2L2≤λΓ‖ekl-1（?，nh）‖2L2，] （16）

[‖ekl（?，nh）‖2L2≤2λG1Γ‖ekl-1（?，nh）‖2L2+2L2g1‖Qkl（?，nh）‖2L2≤ 2λG1Γ‖ekl-1（?，nh）‖2L2+2L2g1λΓφj=0n-1κn-1-j‖ukl（?，jh）‖2L2+][ ][2L2g1κ‖Qkl（?，t0，1）‖2L2.] （17）

對不等式（17）兩邊同時乘[κ-λn]，根據[（L2，λ）]范數的定義，得到

[ ‖ekl‖（L2，λ）≤2λG1Γ‖ekl-1‖（L2，λ）+2L2g1λΓφsupn∈[0，n1]κ-λnj=0n-1κn-1-j‖ekl-1（?，jh）‖2L2+2L2g1supn∈[0，n1]κ-λnκn‖Qkl（?，t0，1）‖2L2， （18）]

式中：

[supn∈[0，n1]κ-λnj=0n-1κn-1-j‖ekl-1（?，jh）‖2L2= κ-1supn∈[0，n1]（j=0n-1κ-λj‖ekl-1（?，jh）‖2L2κ（λ-1）（j-n））≤ κ-1supn∈[0，n1]（j=0n-1supn∈[0，n1]κ-λj‖ekl-1（?，jh）‖2L2κ（λ-1）（j-n））= ‖ekl-1‖（L2，λ）×κ-1supn∈[0，n1]j=0n-1κ（λ-1）（j-n）= ‖ekl-1‖（L2，λ）×1-κ-（λ-1）n1κλ-κ， （19）]

根據式（18）、式（19）可以得到

[‖ekl‖（L2， λ）≤（2λG1Γ+2L2g1λΓφ×1-κ-（λ-1）n1κλ-κ）‖ekl-1‖（L2， λ）.] （20）

根據定理1的條件，取足夠大的[λ]，使下面不等式成立：

[2λG1Γ+2L2g1λΓφ×1-κ-（λ-1）n1κλ-κ≤ρ1<1，]

可得到第一個子系統[limkl→∞‖ekl‖（L2， λ）→0]的結論。

2）當第二個子系統被激活時，[t∈[t1，t2）.]

情況1：在采樣區間內不發生切換，切換序列[α（t）=i]，[t∈[tn1，1，t0，2）]。

[‖Qkl（?，t0，2）‖2L2≤φj=0n1κn1-j‖ukl（?，jh）‖2L2.] （21）

情況2：在采樣區間內發生切換，切換序列[α（t）=i]，[t∈[tn1，1，t1）]；[α（t）=l]，[t∈[t1，t0，2）]。

[‖Qkl（?，t0，2）‖2L2≤κφj=0n1κn1-j‖ukl（?，jh）‖2L2+φ‖ukl（?，n1h）‖2L2.] （22）

在第一個子系統的收斂性的證明中，可以得到[limkl→∞‖ekl‖（L2， λ）→0]的結論，進一步可以得到[limkl→∞‖ukl‖（L2， λ）→0]，依據[（L2，λ）]的定義可以得到[limkl→∞‖ukl（?，ts，1）‖L2→0]。結合對第二個子系統第一個采樣時刻的分析，得出[limkl→∞‖Qkl（?，t0，2）‖L2→0] 。

類似地，根據不等式（20）可以得到

[‖ekl‖（L2， λ）≤（2λG2Γ+2L2g2λΓφ×1-κ-（λ-1）n2κλ-κ）‖ekl-1‖（L2， λ）.] （23）

根據定理1的條件，取足夠大的[λ]，使下面不等式成立：

[2λG2Γ+2L2g2λΓφ×1-κ-（λ-1）n2κλ-κ≤ρ2<1，]

可得到第二個子系統[limkl→∞‖ekl‖（L2， λ）→0]的結論。

以此類推，同樣可以證明在[[t2，t3），… ，[ti-1，T]]上，[‖ekl‖（L2， λ）]收斂到0，即[limkl→∞‖ykl（?，ts，i）-yd（?，ts，i）‖L2→0]。

步驟2 考慮非事件觸發的情況，即[k∈（kl-1，kl）]。當第一個子系統被激活時，

[yk（x，nh）-ykl-1（x，nh）=]

[g1（nh，Qk（x，nh））-g1（nh，Qkl-1（x，nh））.] （24）

進一步可以得到

[‖ykl（?，nh）‖2L2≤L2g1‖Qkl（?，nh）‖2L2，] （25）

式中：[ykl（x，nh）=yk（x，nh）-ykl-1（x，nh）]，[Qkl（x，nh）=Qk（x，nh）-Qkl-1（x，nh）]。

依據不等式（11），同理可得

[‖Qkl（?，nh）‖2L2≤κn‖Qkl（?，t0，1）‖2L2+ φj=0n-1κn-1-j‖ukl（?，jh）‖2L2，] （26）

式中：[ukl（x，nh）=uk（x，nh）-ukl-1（x，nh）]。

對不等式（26）兩邊同時乘[κ-λn]，根據[（L2， λ）]范數的定義，得到

[‖ykl‖（L2， λ）≤κ-λnL2g1φj=0n-1κn-1-j‖ukl（?， jh）‖2L2+ L2g1κ-λnκn‖Qkl（?，t0，1）‖2L2≤ L2g1φ‖ukl‖（L2， λ）×1-κ-（λ-1）n1κλ-κ. （27）]

在同一迭代批次中，非事件觸發時刻的系統輸入保持不變；事件觸發時刻的系統輸入[limkl→∞‖ukl‖（L2， λ）→0]。因此可知[limkl→∞‖ukl‖（L2， λ）→0]，進一步得到[limkl→∞‖ykl‖（L2， λ）→0]。以此類推，同樣可以證明在[[t1，t2），… ，[ti-1，T]]上[limkl→∞‖ykl‖（L2， λ）→0]。依據[（L2， λ）]的定義可以得到[limkl→∞‖yk（?，ts，i）-ykl-1（?，ts，i）‖L2→0]，[i=1，2，… ，m]。

總結上述步驟1和步驟2可知，系統的輸出將隨著事件觸發迭代學習收斂到0，而在非事件觸發情況下，系統的輸出將會沿上一次事件觸發的系統輸出收斂。

3 仿真算例

本節通過一個數值仿真的例子來驗efe2e6023ab8dbef5a22ce5ac4d48dba81a6da61f505c57fc7fc882efe51057f證分布參數切換系統事件觸發采樣迭代學習控制的有效性。考慮具有2個子系統的分布參數切換系統，其相對應的參數如下：

[f1（x，t）=1.5sin t0.20.8-2.5cos（Qk，1（x，t））cos（Qk，2（x，t））+]

[-1.1e-t0.80.2-1.3][ uk，1（x，t）uk，2（x，t），]

[f2（x，t）=1.50.8cos t0.5-2cos（Qk，1（x，t））cos（Qk，2（x，t））+]

[-0.50.50-1.5sin tuk，1（x，t）uk，2（x，t）][ ，]

[g1（x，t）=0.61.3cos t0.62.4sin（Qk，1（x，t））sin（Qk，2（x，t））][ ，]

[g2（x，t）=0.510.9e-t2sin（Qk，1（x，t））sin（Qk，2（x，t））][ ，]

[G1=-cos t00-1][ ，]

[G2=-cos t00-1][ ，]

式中：[（x，t）∈[0，1]×[0，1]]。給定參數[β=0.995]，[Γ=[0.8 0;0 0.5]]。2個子系統之間的切換規則如圖1所示。

給出期望軌跡的表達式：

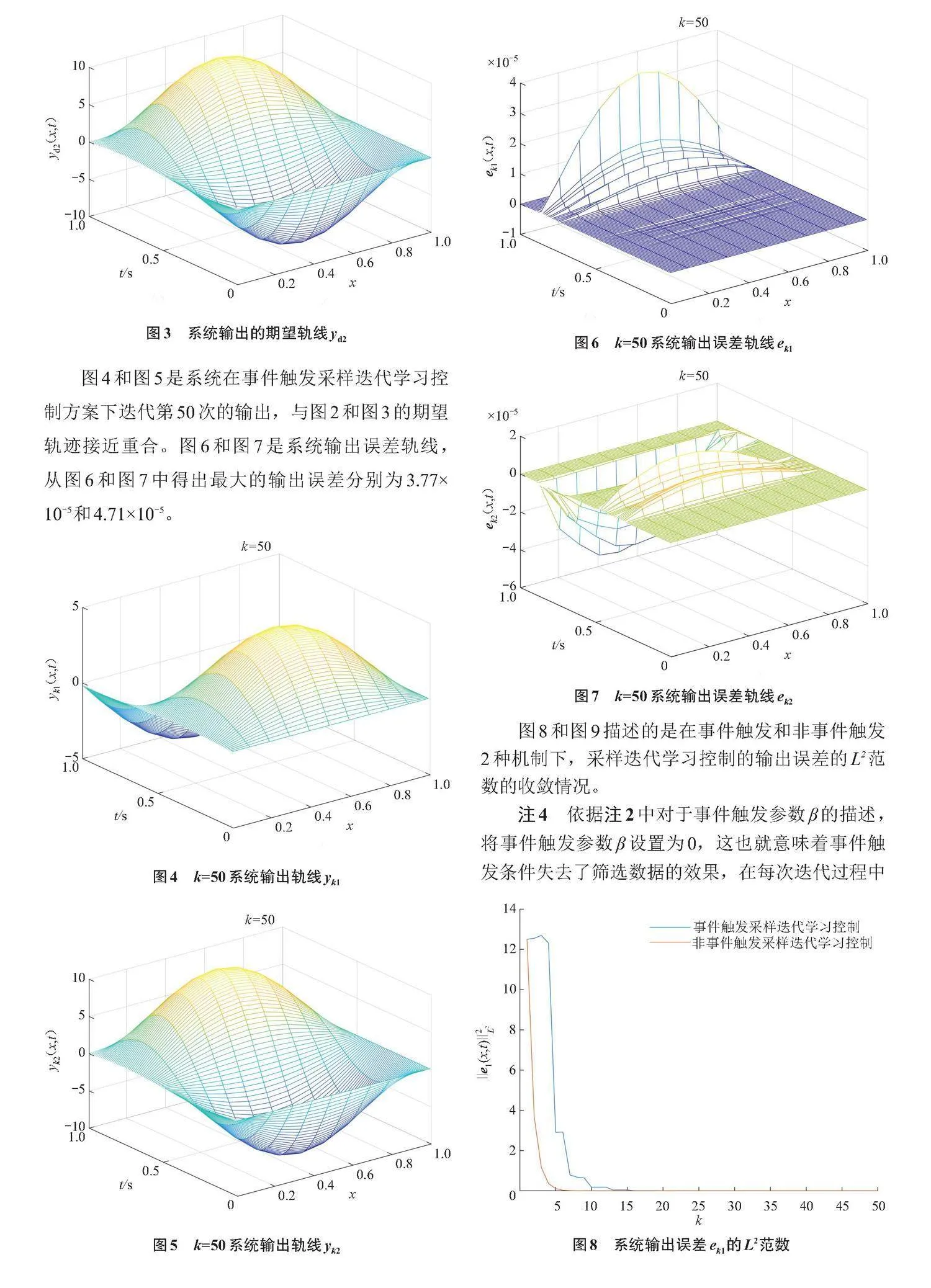
[yd（x，t）=5sin（5t）sin（πx）-10sin（2πt）sin（πx）.]

該期望軌線如圖2和圖3所示。

圖4和圖5是系統在事件觸發采樣迭代學習控制方案下迭代第50次的輸出，與圖2和圖3的期望軌跡接近重合。圖6和圖7是系統輸出誤差軌線，從圖6和圖7中得出最大的輸出誤差分別為3.77×10-5和4.71×10-5。

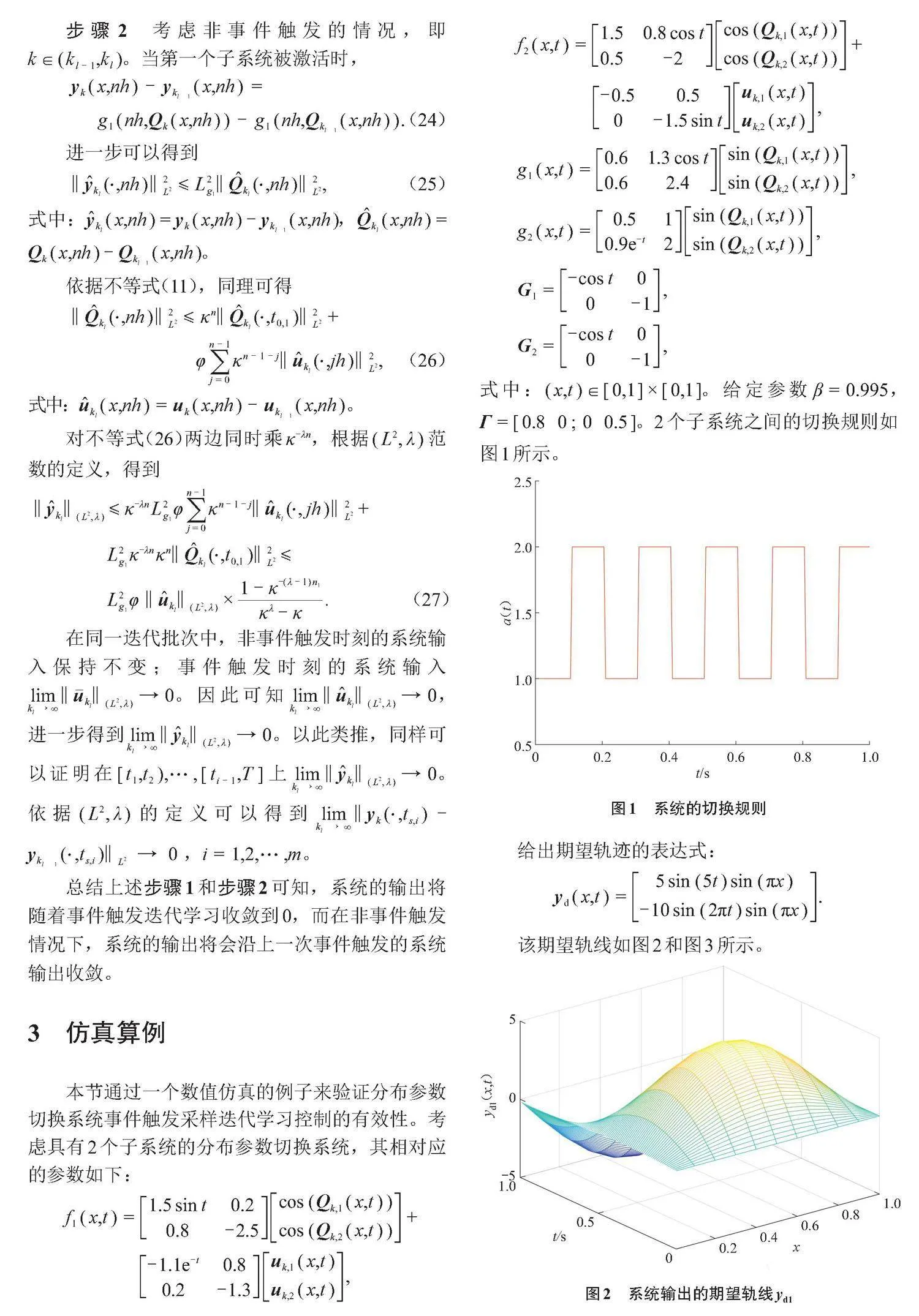
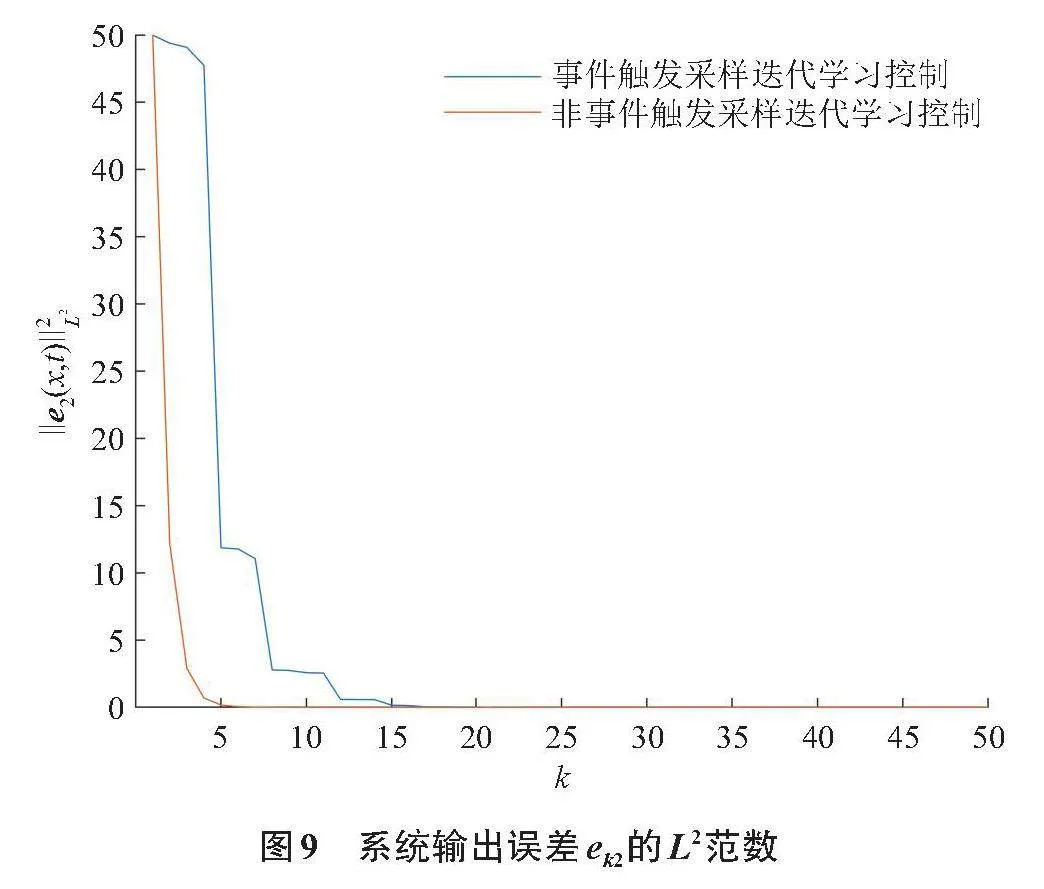
圖8和圖9描述的是在事件觸發和非事件觸發2種機制下，采樣迭代學習控制的輸出誤差的L2范數的收斂情況。

注4 依據注2中對于事件觸發參數[β]的描述，將事件觸發參數[β]設置為0，這也就意味著事件觸發條件失去了篩選數據的效果，在每次迭代過程中控制器在所有采樣時刻都進行學習、更新，因此得到非事件觸發采樣迭代學習控制，也就是傳統的采樣迭代學習控制。

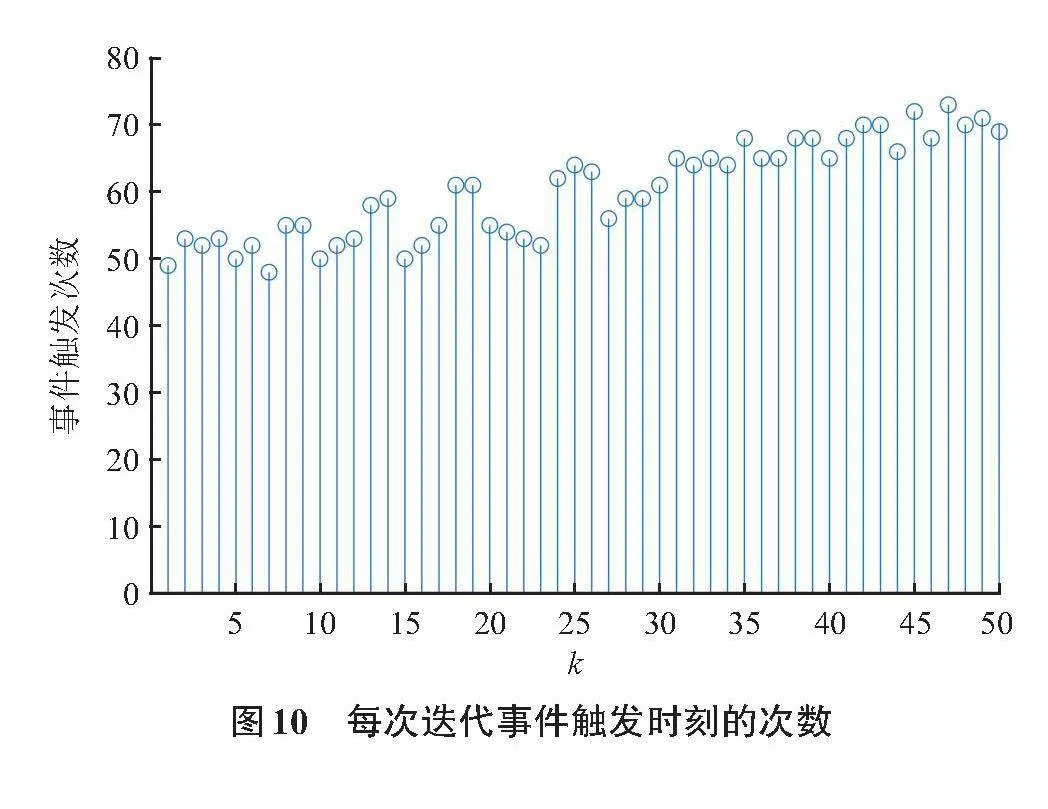
對比事件觸發采樣迭代學習和非事件觸發采樣迭代學習2種方案下的系統輸出誤差（圖8和圖9），可以看到，2種方案都可以使得系統的輸出誤差趨向于0，這意味著在2種控制方案下都可以使得系統輸出漸進趨向于期望軌跡。圖10表示在50次迭代過程中每一次迭代學習發生事件觸發的采樣時刻的數量，即相鄰2次迭代之間控制器更新的數量，沒發生事件觸發的采樣時刻也就意味著減少了控制器的更新，節省了資源。通過計算得出在50次迭代中，事件觸發采樣迭代學習控制相比于非事件觸發采樣迭代學習控制節約了39.8%。

注5 從圖8和圖9中看出，雖然事件觸發采樣迭代學習控制的輸出誤差的收斂速度相比于非事件觸發采樣迭代學習控制而言會相對較慢，但是仍然能夠使得系統收斂到期望軌跡上。相比于輸出誤差的收斂速度變慢，事件觸發采樣迭代學習控制能夠有效地節約每一次迭代學習控制器的更新。

4 結論

本文針對非線性分布參數切換系統，提出了一種基于事件觸發機制的采樣迭代學習控制算法，并利用Lyapunov函數設計事件觸發條件。當滿足事件觸發條件時，控制器采用開環學習律對事件觸發的采樣時刻的控制輸出進行更新學習。在事件觸發和非事件觸發2種情況下，對非線性分布參數切換系統事件觸發采樣迭代學習控制的收斂性進行了嚴格的分析。最后，通過數值仿真驗證了文中提出的事件觸發采樣迭代學習控制在節省資源方面的優勢。

參考文獻

[1] OOBA T，FUNAHASHI Y. On a common quadratic Lyapunov function for widely distant systems[J]. IEEE Transactions on Automatic Control，1997，42（12）：1697-1699.

[2] BALLUCHI A，DI BENEDETTO M D，PINELLO C，et al.Hybrid control in automotive applications：the cut-off control[J]. Automatica，1999，35（3）：519-535.

[3] LENNARTSON B，TITTUS M，EGARDT B，et al.Hybrid systems in process control[J]. IEEE Control Systems Magazine，1996，16（5）：45-56.

[4] LI S，AHN C K，CHADLI M，et al.Sampled-data adaptive fuzzy control of switched large-scale nonlinear delay systems[J]. IEEE Transactions on Fuzzy Systems，2021，30（4）：1014-1024.

[5] SANG H，ZHAO J.Passivity and passification for switched T-S fuzzy systems with sampled-data implementation[J]. IEEE Transactions on Fuzzy Systems，2020，28（7）：1219-1229.

[6] YANG T，HUANG X，WANG Z，et al.Aperiodic sampled-data synchronization of Markovian jump neural networks with partially known switching transition rates[J]. Communications in Nonlinear Science and Numerical Simulation，2023，126：107448.

[7] GUAN C X，CHEN W Z，YANG L，et al.Sampled-data asynchronous control for switched nonlinear systems with relaxed switching rules[J]. IEEE Transactions on Cybernetics，2022，52（11）：11549-11560.

[8] ZOU W C，GUO J，AHN C K，et al.Sampled-data consensus protocols for a class of second-order switched nonlinear multiagent systems[J]. IEEE Transactions on Cybernetics，2023，53（6）：3726-3737.

[9] TARN T J，ZAVGREN J R JR，ZENG X M.Stabilization of infinite-dimensional systems with periodic feedback gains and sampled output[J]. Automatica，1988，24（1）：95-99.

[10] TAN Y，NE?I? D.Sampled-data output feedback control of distributed parameter systems via semi-discretization in space[J]. IFAC Proceedings Volumes，2008，41（2）：7749-7754.

[11] FRIDMAN E，BAR AM N.Sampled-data distributed H∞ control of a class of parabolic systems[C]//2012 IEEE 51st IEEE Conference on Decision and Control （CDC）.Maui，HI，USA. 2012：7529-7534.

[12] WANG Z P，WU H N.Finite dimensional guaranteed cost sampled-data fuzzy control for a class of nonlinear distributed parameter systems[J]. Information Sciences，2016，327：21-39.

[13] WANG Z P，WU H N，WANG X H.Sampled-data control for linear time-delay distributed parameter systems[J]. ISA Transactions，2019，92：75-83.

[14] WANG J W，LI H X，WU H N.A membership-function-dependent approach to design fuzzy pointwise state feedback controller for nonlinear parabolic distributed parameter systems with spatially discrete actuators[J]. IEEE Transactions on Systems，Man，and Cybernetics：Systems，2017，47（7）：1486-1499.

[15] 梅三各，戴喜生，余莎麗，等.高相對度非正則離散拋物分布參數系統迭代學習控制[J]. 廣西科技大學學報，2019，30（1）：31-38.

[16] CHIEN C J.The sampled-data iterative learning control for nonlinear systems[C]//Proceedings of the 36th IEEE Conference on Decision and Control.San Diego，CA，USA，1997：4306-4311.

[17] SUN M X，WANG D W.Sampled-data iterative learning control for nonlinear systems with arbitrary relative degree[J]. Automatica，2001，37（2）：283-289.

[18] 姚仲舒，楊成梧.時滯非線性系統的采樣迭代學習控制[J]. 控制理論與應用，2003，20（3）：459-463.

[19] CHI R H，HUI Y，CHIEN C J，et al.Convergence analysis of sampled-data ILC for locally lipschitz continuous nonlinear nonaffine systems with nonrepetitive uncertainties[J]. IEEE Transactions on Automatic Control，2021，66（7）：3347-3354.

[20] ASTROM K J，BERNHARDSSON B M.Comparison of Riemann and Lebesgue sampling for first order stochastic systems[C]//Proceedings of the 41st IEEE Conference on Decision and Control.Las Vegas，NV，USA，2002：2011-2016.

[21] 張海江，文家燕，謝廣明，等.飽和約束下事件觸發多智能體系統量化通信環形編隊控制[J]. 廣西科技大學學報，2022，33（4）：44-50，69.

[22] LI H Y，LIN N，CHI R H.Event-triggered iterative learning control for linear time-varying systems[J]. International Journal of Systems Science，2022，53（5）：1110-1124.

[23] LIN N，CHI R H，HUANG B，et al.Event-triggered nonlinear iterative learning control[J]. IEEE Transactions on Neural Networks and Learning Systems，2021，32（11）：5118-5128.

[24] 余威，卜旭輝，梁嘉琪.基于二維系統的迭代學習事件觸發魯棒控制[J]. 控制理論與應用，2020，37（8）：1701-1708.

[25] QI Y W，QU Z Y，YAO Z H，et al.Event-triggered iterative learning control for asynchronously switchedb5235d9da7ea93b8c180f8632809042f systems[J]. Applied Mathematics and Computation，2023，440：127662.

[26] ZHANG T，LI J M.Event-triggered iterative learning control for multi-agent systems with quantization[J]. Asian Journal of Control，2018，20（3）：1088-1101.

[27] WANG L M，ZHANG G S.Event-triggered iterative learning control for perfect consensus tracking of non-identical fractional order multi-agent systems[J]. International Journal of Control，Automation and Systems，2021，19（3）：1426-1442.

[28] HUA C C，QIU Y F，GUAN X P. Event-triggered iterative learning containment control of model-free multiagent systems[J]. IEEE Transactions on Systems，Man，and Cybernetics：Systems，2021，51（12）：7719-7726.

[29] ZHAO H R，YU H N，PENG L.Event-triggered distributed data-driven iterative learning bipartite formation control for unknown nonlinear multiagent systems[J]. IEEE Transactions on Neural Networks and Learning Systems，2022，42（6）：256-263.

[30] 趙華榮，彭力，謝林柏，等.多智能體系統的事件觸發無模型迭代學習雙向一致性[J]. 控制與決策，2022，37（10）：2552-2558.

[31] LIN N，CHI R H，HUANG B.Event-triggered ILC for optimal consensus at specified data points of heterogeneous networked agents with switching topologies[J]. IEEE Transactions on Cybernetics，2022，52（9）：8951-8961.

[32] 王宏偉，李昊哲.數據丟包下事件驅動的非線性多智能體迭代學習控制[J]. 控制理論與應用，2022，39（9）：1688-1698.

[33] WANG Q，JIN S T，HOU Z S.Event-triggered cooperative model-free adaptive iterative learning control for multiple subway trains with actuator faults[J]. IEEE Transactions on Cybernetics，2023，53（9）：6041-6052.

[34] LI H Y，LUO J H，MA H，et al. Observer-based event-triggered iterative learning consensus for locally lipschitz nonlinear MASs[J]. IEEE Transactions on Cognitive and Developmental Systems，2024，16（1）：46-56.

Event-triggered sampled iterative learning control for nonlinear

distributed parameter switched system

SHENG Chengxiang1， 2 ， DAI Xisheng*1， 2

（1. School of Automation， Guangxi University of Science and Technology， Liuzhou 545616， China; 2. Institute of Intelligent Systems and Control（Guangxi University of Science and Technology）， Liuzhou 545616， China）

Abstract： In this paper， we studied the event-triggered sampled iterative learning control problem for a nonlinear distributed parameter switched system. Based on the sampling of the system input and system output， the method of Lyapunov function was used to obtain the event-triggered conditions， and the controller would be updated when the event-triggered conditions were satisfied， which effectively reduced the update of the controller in the iterative learning process. The convergence of the event-triggered sampled iterative learning control was proved through strict mathematical derivation. The effectiveness of the algorithm was verified by numerical simulation experiments.

Keywords： distributed parameter switched system; data sampling; iterative learning control; event-triggered

（責任編輯：黎 婭）

收稿日期：2023-10-19；修回日期：2024-01-05

基金項目：國家自然科學基金項目（62363002，61863004）資助

第一作者：盛程相，在讀碩士研究生

*通信作者：戴喜生，博士，教授，研究方向：分布參數系統迭代學習控制，E-mail：mathdxs@163.com