多吸引子憶阻混沌系統在圖像加密中的應用

【摘 要】 為增強圖像加密安全性，基于Lorenz混沌系統設計了一種新型的多吸引子憶阻混沌系統。通過最大李雅普諾夫指數圖、分岔圖和雙參復雜度圖進行理論分析和仿真，結果顯示該系統具有共存吸引子現象，驗證了系統具有超混沌特點及對初始值的高敏感性。此外，利用該系統在高復雜度區間生成的混沌序列對圖像矩陣進行擴散、置亂、旋轉及循環處理，實現圖像的加密。通過直方圖、信息熵及相鄰像素相關性分析，證實了該算法具有較高的加密性能。

【關鍵詞】 多吸引子憶阻混沌系統；共存吸引子；圖像加密

Application of Multi-attractor Memristor Chaotic System in Image Encryption

Dai Wenpeng1， Chen Heng2*， Song Li1， He Na1， Yang Hongyu1

（1.Yantai Institute of Science and Technology， Yantai 265600， China;

2.Xijing University， Xi′an 710123， China）

【Abstract】 In order to enhance the security of image encryption， a new multi-attractor memristor chaotic system based on Lorenz chaotic system is designed. Through the theoretical analysis and simulation of the maximum Lyapunov exponent graph， the bifurcation graph and the two-parameter complexity graph， the author draws the conclusion that the system has the coexistence attractor phenomenon， and it is verified that the system is hyperchaotic and highly sensitive to the initial value. In addition， the chaotic sequence generated by the system in the high complexity region is used to diffuse， scramble， rotate and cycle the image matrix， so as to realize the image encryption. Through the analysis of histogram， information entropy and the correlation of adjacent pixels， the author confirms that the algorithm has high encryption performance.

【Key words】 muti-attractor memristor chaotic system; coexisting attractors; image encryption

〔中圖分類號〕 TN601 〔文獻標識碼〕 A 〔文章編號〕 1674 - 3229（2024）03 - 0060 - 08

0 引言

多吸引子混沌系統結合了具有記憶性的憶阻器，增加了系統的隨機性和不可預測性，從而使得系統的動態行為更為復雜［1-2］。由于混沌序列的復雜性，系統更難被攻擊者預測，有效增強了抗攻擊能力。同時，由于數字圖像像素之間的強關聯性，混沌系統應用于圖像加密中，可以有效打破這種關聯性，從而進一步提高密文的抗攻擊性［3-6］。因此，對Lorenz混沌系統進行模擬和改進，以提高系統復雜度，并將改進后的系統與加密算法相結合，不僅增強了像素的隨機性，也為提高加密算法的安全性提供了新的思路，顯示出該系統在圖像加密領域的重要應用價值。

首先，通過引入正弦函數、憶阻器到模擬Lorenz系統中，構建了多吸引子憶阻混沌系統。使用Matlab進行數值計算和仿真，驗證了該系統能夠根據初始條件及參數變化顯示出復雜的動態行為。其次 ，利用該系統在高復雜度區間生成的混沌序列，執行圖像加密過程中的各種操作，包括擴散、置亂、旋轉和循環運算，此操作有助于破壞圖像數據中像素之間原有的關聯性，從而實現圖像的有效加密［7-8］。最后，通過對加密圖像信息熵、直方圖及相關性分析，表明該系統的算法復雜性強，能夠顯著提高圖像加密的安全性能。

1 多吸引子憶阻混沌系統

杜傳紅［9］替換Lorenz系統非線性項，使用絕對值函數和雙極轉換常數，模擬出Lorenz系統：

[x=a（y-x）y=（c-z） sign （x）z=|x|-bz] （1）

分段二次型有源磁控憶阻器模型為：

[q（φ）=-aφ+0.5φ2sgn（φ）]

憶導為：

[w（φ）=dq（φ）dφ=-a+b|φ|] （2）

對于系統（1），引入正弦信號及憶阻器模型（2），構建新的多吸引子憶阻混沌系統：

[x=a（y-x）+0.5sign（sin（0.05t））y=（c-z） sign （x）z=w|x|-bzw=-k1|z|+k2w] （3）

系統初值[x0=0.1]、[y0=0.1]、[z0=1]、[w0=3]，系統參數[a=1.2]、[b=1.8]、[c=2]、[k1=0.1]、[k2=0.2]、[m=5]、[n=0.2]時，系統（3）相圖如圖1所示，顯示存在2個混沌吸引子。計算得到該系統的李雅普諾夫指數（LE）分別為[λ1=0.336]、[λ2=0.304]、[λ3=-1.005]、[λ4=-2.035]，有兩個正的LE，說明系統（3）具有超混沌特性。

2 平衡點及共存吸引子分析

將系統（3）設為零，分析該系統在沒有加入脈沖信號時的平衡點：

[a（y-x）=0（c-z）sign（x）=0w|x|-bz=0-k1|z|+k2w=0] （4）

得出平衡點為：

[E1=（0，0，0，0）]、[E2=（0.08，0.08，2，-0.2）]。

加入脈沖信號[signsin（0.05t）]時：

[a（y-x）+0.5signsin（0.05t）=0（c-z）sign（x）=0w|x|-bz=0-k1|z|+k2w=0] （5）

得出平衡點為：

[E3=（0，0±0.42，0，0）]、[E4=（0.08，0.08±0.42，2，-2）]。

通過公式（4）、（5）結果對比，發現系統（3）平衡點在[y]方向上平移了±0.42個單位，說明該系統的動態性較強。從圖2（a）系統在[y]軸上的時序圖中可以看出，虛線代表的脈沖信號對系統產生了顯著影響。在脈沖信號的控制下，[y]方向的波形沿著脈沖信號上下移動，振幅在±2之間，振蕩中心在大約±0.42之間。表明脈沖信號使得系統的平衡點沿著[y]軸方向發生了±0.42個單位的平移。圖2（b）的相圖俯視圖進一步驗證了這一結果，相圖清晰地展示了在脈沖信號作用下，系統在相空間中的軌跡發生了顯著變化，引發了多吸引子混沌現象的出現，表明系統的動力學行為變得更加豐富。

當[a=1.2]、[b=1.8]、[c=2]、[k1=0.1]、[k2=1]、[m=5]、[n=0.2]、[x0=0]、[y0=0.1]、[z0=±1]、[w0=3]時，系統出現共存混沌吸引子，如圖3（a）所示；取[b=4]，出現共存周期吸引子，如圖3（b）所示，說明系統受初值影響敏感。

3 系統參數分析

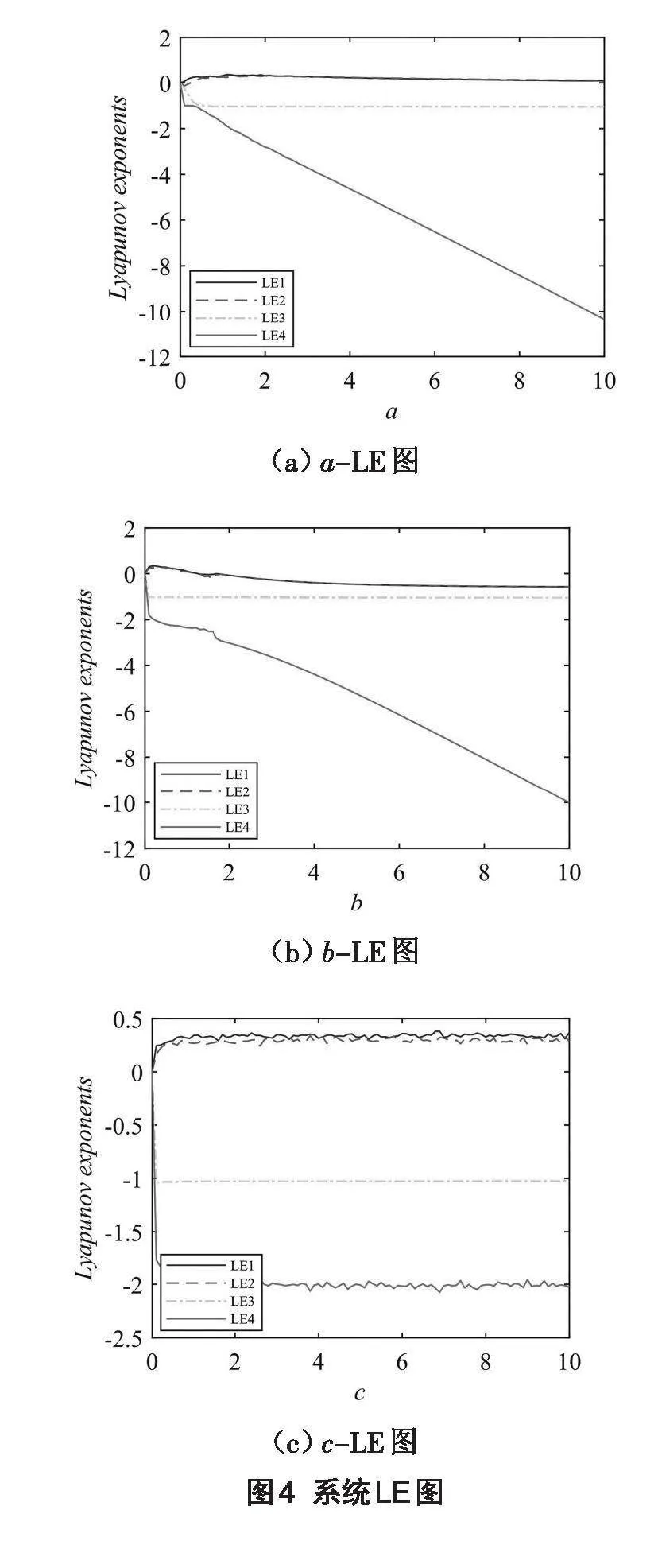
首先，研究模擬Lorenz系統參數[a]、[b]、[c]在4個方向上的LE圖，如圖4所示。系統（3）變量分別設定為特定值時發現：僅參數[a]發生變化時，系統處于弱混沌狀態，如圖4（a）；僅參數[b]發生變化時，系統在[b∈[0，2）]上展現出混沌態，在[b∈[2，10]]上為周期態，如圖4（b）；僅參數[c]變化時，系統則進入超混沌態，如圖4（c）。鑒于高復雜度的混沌序列能夠增強圖像927c5c9b953d5c2a1c056599d7c88ccf加密的安全性。因此，所選定的參數值[a=1.2]、[b=0.2]、[c=2]符合該要求。

為更好地研究憶阻器相關參數對系統的影響，繪制了系統（3）在4個方向上的LE圖、分岔圖以及雙參數復雜度圖。當參數[k1]單一變化時，系統呈現超混沌狀態，具體如圖5（a）、5（b）所示；當參數[k2]單一變化時，系統同樣為超混沌狀態，如圖5（c）、5（d）所示；當[m]單一變化時，系統在[m=0.2]附近為周期狀態，而其余區間則為超混沌態，具體如圖5（e）、5（f）所示；最后，當參數[n]單一變化時，系統再次呈現超混沌狀態，具體如圖5（g）、5（h）所示。說明憶阻器的引入，系統整體呈現為超混沌態，提高了系統的復雜度。因此，選擇復雜性較強的參數[k1=0.1]、[k2=0.5]、[m=5]、[n=0.2]，作為后續加密應用的參數。

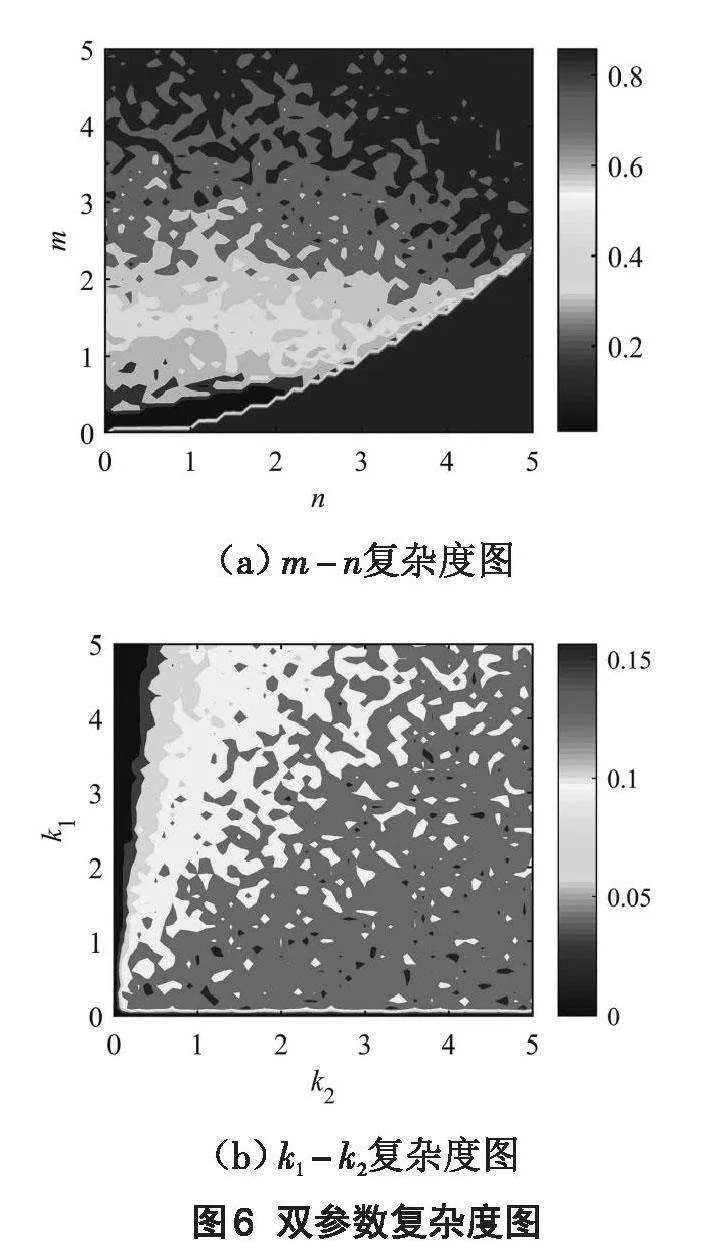
當[a=1.2]、[b=1.8]、[c=2]、[k1=0.1]、[k2=0.2]時，做系統（3）的[m-n]雙參數復雜度狀態圖。其中，暗紅色部分代表復雜度最高，橙色部分代表復雜度較高，黃色部分代表復雜度一般，綠藍色部分代表復雜度較低，如圖6（a）所示。當[m=5]時，[n∈[0，5]]區間復雜度相似且為強復雜區，與圖5（h）關于的[n]單參數LE變化一致。當[n=0.2]，[m∈[0，5]]區間復雜度呈上升趨勢，且在[m=5]處復雜度較強，與圖5（f）關于[m]的單參數LE變化一致。

當[a=1.2]、[b=1.8]、[c=2]、[m=5]、[n=0.2]時，系統（3）的[k1-k2]雙參數復雜度圖見如圖6（b）。當[k1=0.1]時，[k2∈[0，5]]區間復雜度相似且為強復雜區，與圖5（d）關于[k2]的單參數LE變化一致。當[k2=0.2]，[k1∈[0，5]]區間復雜度呈微弱下降趨勢，且在[k1=5]處復雜度相對較小，與圖5（b）關于[m]的單參數LE變化一致。

從圖6得出[k1=0.1]、[k2=0.2]、[m=5]、[n=0.2]在強復雜度區間內，為后續加密參數的設定提供依據。

綜上所述，系統參數采用[a=1.2]、[b=0.2]、[c=2]、[k1=0.1]、[k2=0.5]、[m=5]、[n=0.2]，系統初值采用[x0=0.1]、[y0=0.1]、[z0=1]、[w0=3]，應用于后續圖像加密中，混沌序列復雜性較高，使加密后的圖像破解難度增加，更具有安全性。

4 圖像加密仿真及安全驗證

4.1 加密方案

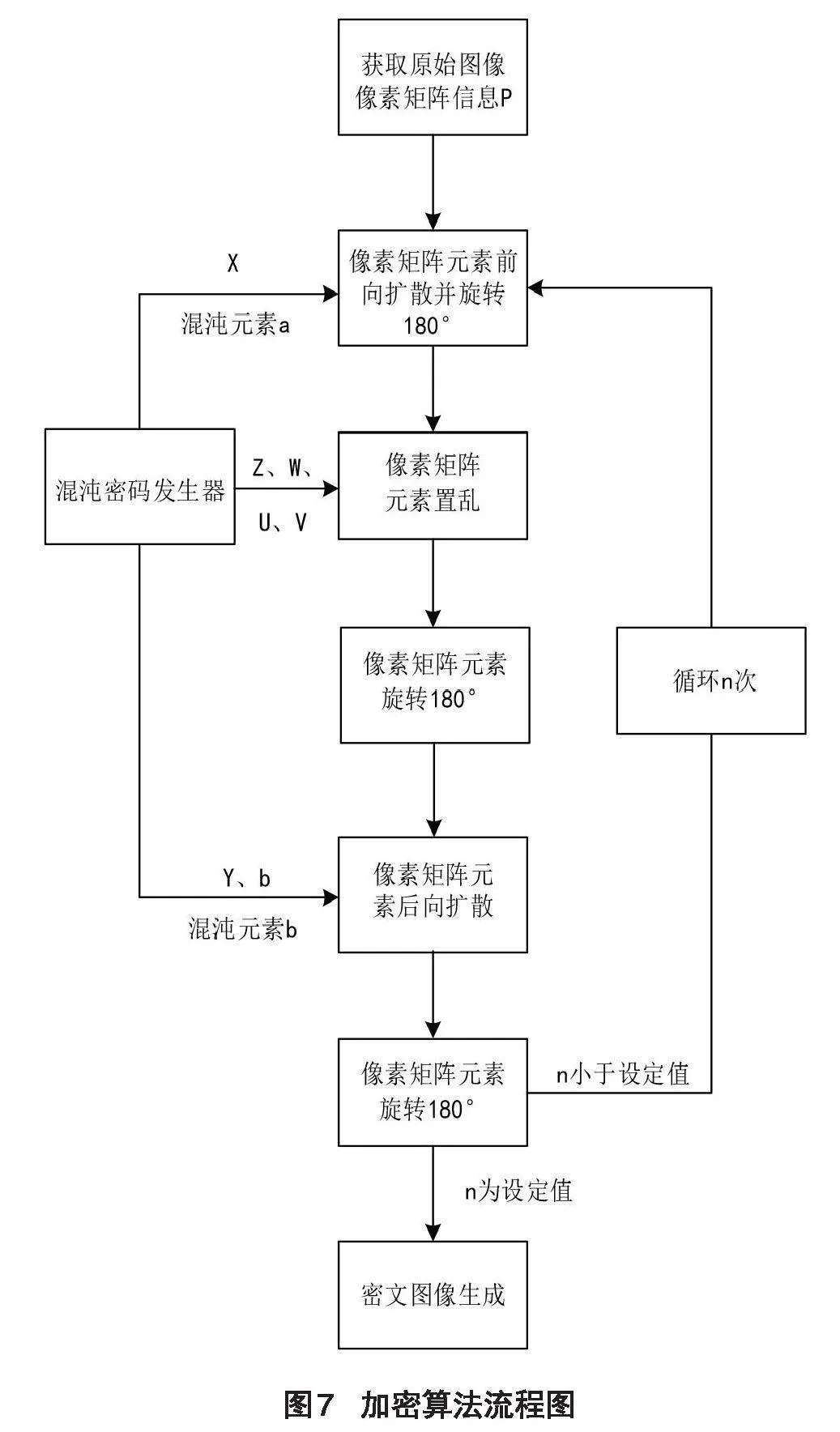
系統加密方案如圖7所示，具體流程為：

Step1：讀取原始圖像信息，獲取圖像矩陣像素值；設定初始值（密鑰[x0]、[y0]、[z0]、[w0]）及系統參數，利用多吸引子混沌系統產生X、Y、Z、W、U、V混沌矩陣及混沌元素a、b。

Step2：將X混沌矩陣及混沌元素a與圖像矩陣P進行異或運算，將前向擴散后的矩陣旋轉180°并通過Z、W、U、V混沌矩陣進行圖像矩陣位置的置亂，將得到的矩陣旋轉180°，形成新的矩陣。

Step3：將Y混沌矩陣及混沌元素b與Step2得到的圖像矩陣進行異或運算，得到的矩陣后向擴散并旋轉180°輸出加密矩陣。根據設定值n進行以上工序的進步加密，輸出加密圖片。

4.2 解密方案

解密過程是加密過程的逆過程，首先授權用戶使用相同的混沌序列對加密后的矩陣像素值進行逆向替換，然后再進行逆向置換，最終恢復出原始圖像，具體流程如圖8所示。

Step1：讀取密圖圖像信息，獲取圖像矩陣元素值；配置初始值（密鑰[x0]、[y0]、[z0]、[w0]），利用多吸引子混沌系統產生X、Y、Z、W、U、V混沌矩陣及混沌元素a、b。

Step2：將旋轉180°后的Y混沌矩陣同混沌元素b與密圖矩陣C進行前向擴散，將擴散后的矩陣旋轉180°。輸出的矩陣通過變化后的Z、W、U、V混沌矩陣進行元素位置的置亂，將置亂后的矩陣旋轉180°，根據設定值n進行工序的進一步循環，輸出原始圖片。

4.3 算法驗證及圖像直方圖分析

采用基于多吸引子的圖像加密算法對雪景原圖加密，加密后的雪景密圖如圖9（b）所示，經該算法得到的雪景解密圖如圖9（c）所示。圖9（a）雪景原圖與雪景解密圖一致，實現了圖像信息加密及解密。為進一步驗證該算法的有效性，從圖像內在的像素值分布情況進行分析，根據圖10（a）原圖像素值分布情況，得出原圖像素值分布隨機性弱，像素值具有一定的關聯性，數學統計特性強。根據圖10（b）密圖像素值分布情況，得出密圖像素值分布具體高度隨機性，像素值關聯性很弱，數學統計特性不明顯。根據圖10（c）解密圖像素值分布情況，得出解密圖像素值分布情況與10（a）原圖像素值分布情況基本一致。充分驗證了該算法的有效性。

圖像直方圖是對像素數據統計的一種方法，用以表示圖像灰度值的像素數分布情況［9-10］。橫坐標表示灰度值，縱坐標表示該灰度值出現的頻次。原圖像的灰度頻次分布不均勻且統計特性明顯，如圖11（a）所示，密圖的灰度頻次分布更均勻，且直方圖統計特性不明顯，如圖11（b）所示。說明該算法具有抗統計攻擊特性。

4.4 信息熵及相關性分析

信息熵值反映像素值混亂程度，信息熵越大時像素值越亂，反之越小［11］。經計算得出原圖信息熵為7.4531，密文信息熵為7.9999，接近理論值8，加密效果較好。為研究像素相鄰元素相關性，對原始圖片及加密圖片進行像素值相關性分析，相關性計算公式為：

[ρx，y=cov（x，y）D（x）+D（y）] （6）

其中：

[D（x）=1Ni=1Nxi-E（x）2]，[D（y）=1Ni=1Nyi-E（y）2]

[cov（x，y）=E（x-E（x））（y-E（y））]。

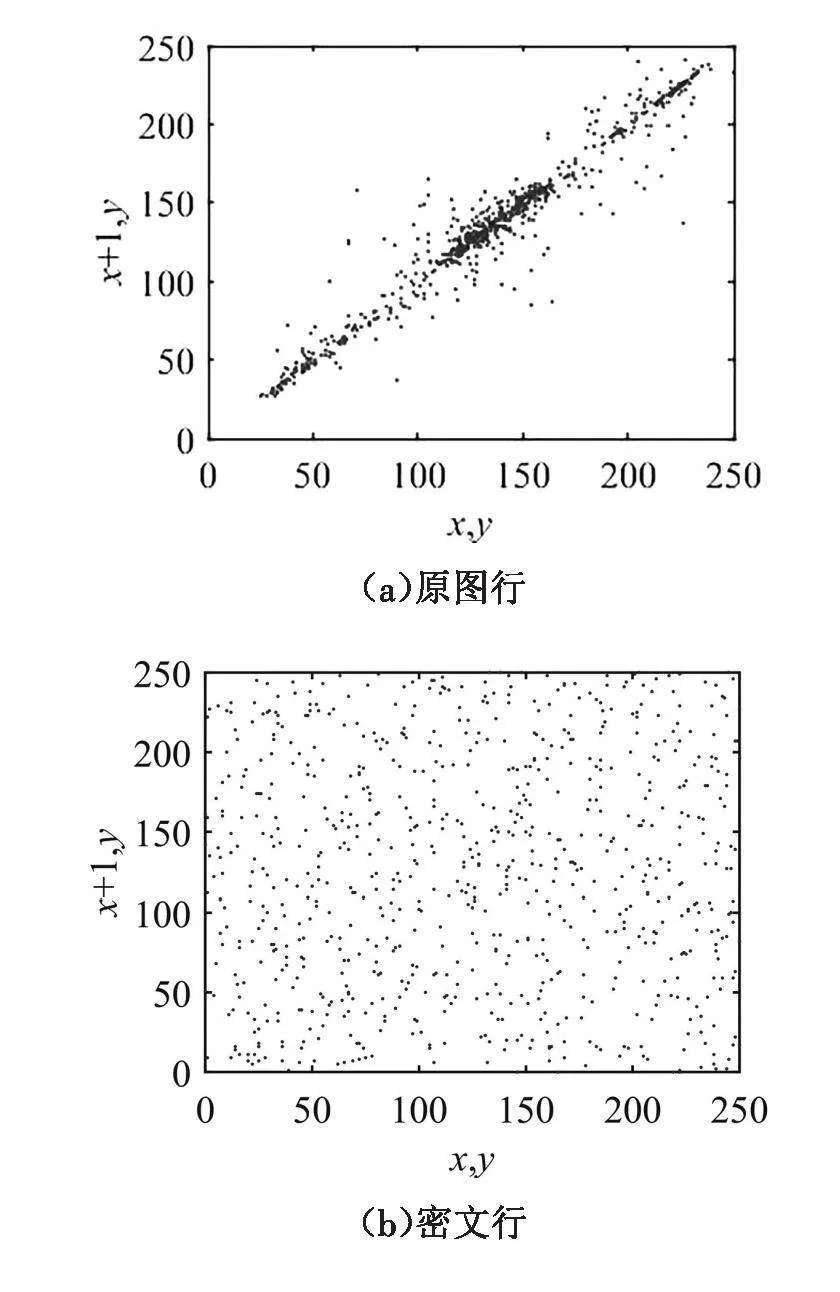
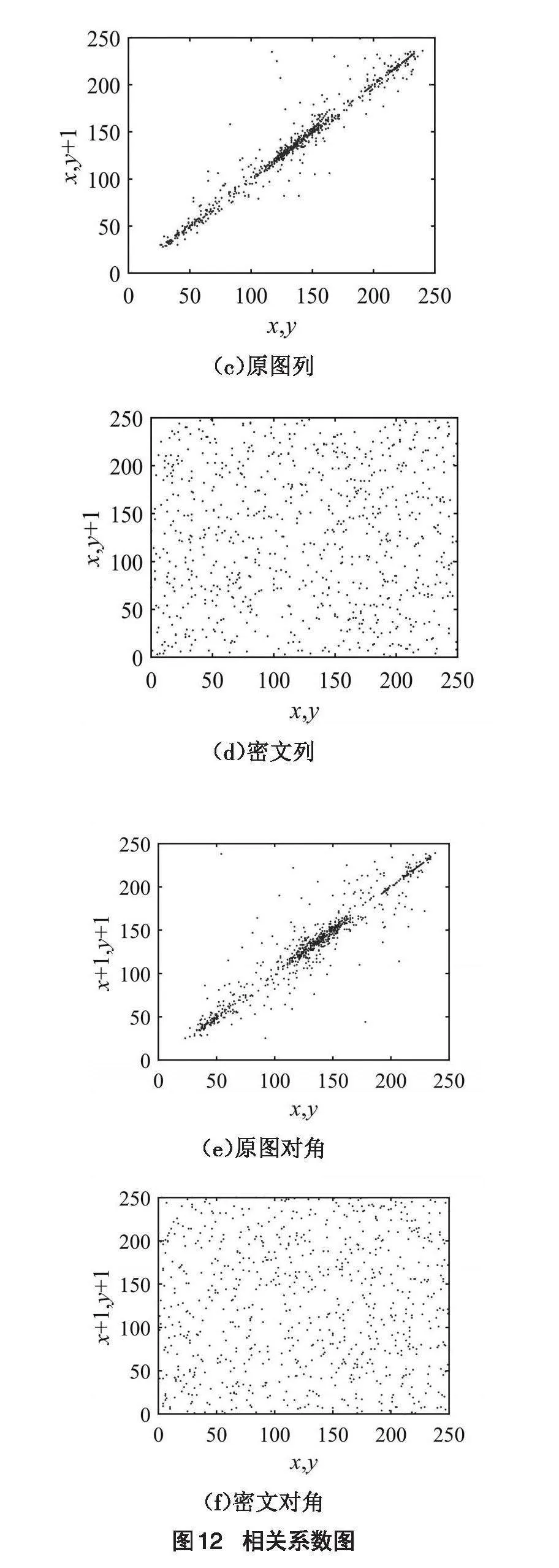
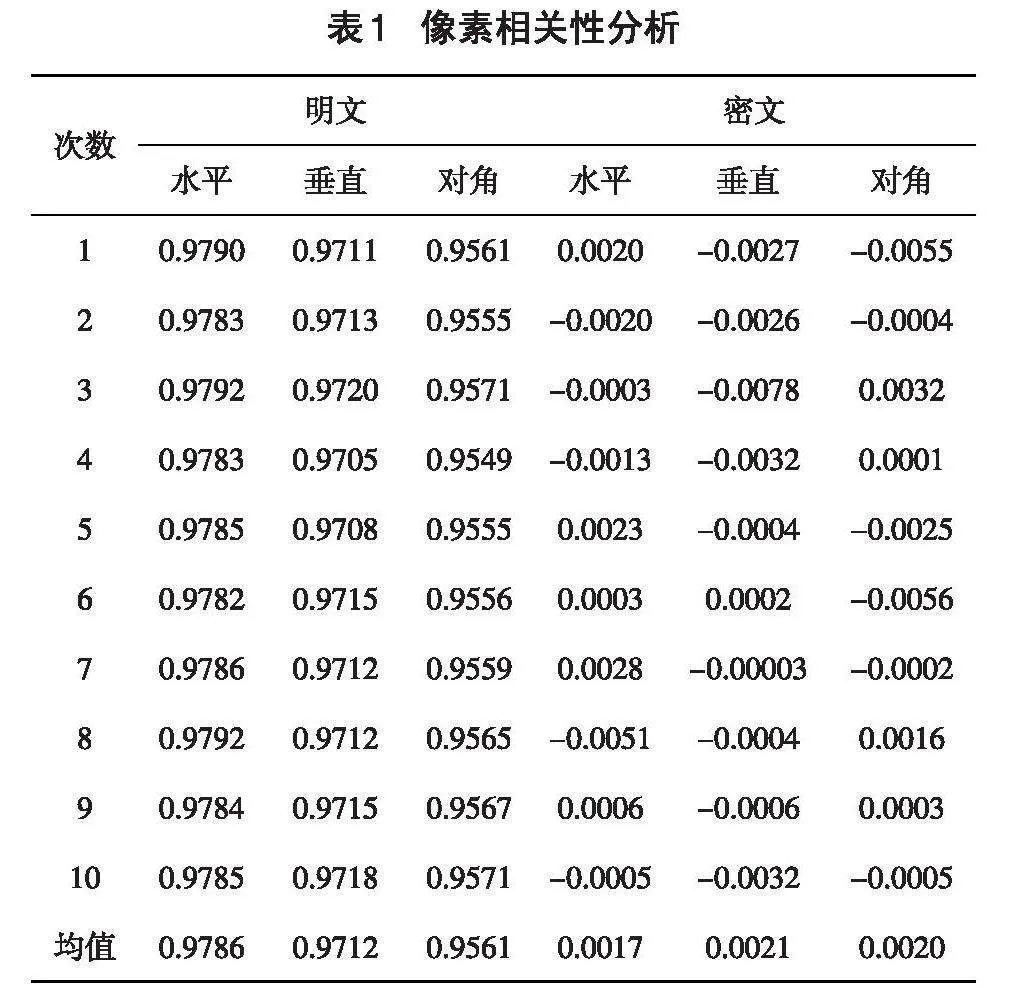
隨機抓取10次，進行絕對平均值處理，每次統計10000個像素點的相關系數值，如表1所示。原圖行、列、對角方向的相關系數為0.9786、0.9713、0.9561，密圖相關系數為0.0017、0.0021、0.0020。結果表明，經該算法加密后，圖片矩陣像素值相關性較低，加密算法有效。

圖像化直觀展示相關性，由圖12（a），12（c），12（e）可知，原圖像素間相關性顯著，由圖12（b），12（d），12（f）可知，密圖像素間相關性弱。說明該算法能夠有效降低相關性，提高圖像加密性能。

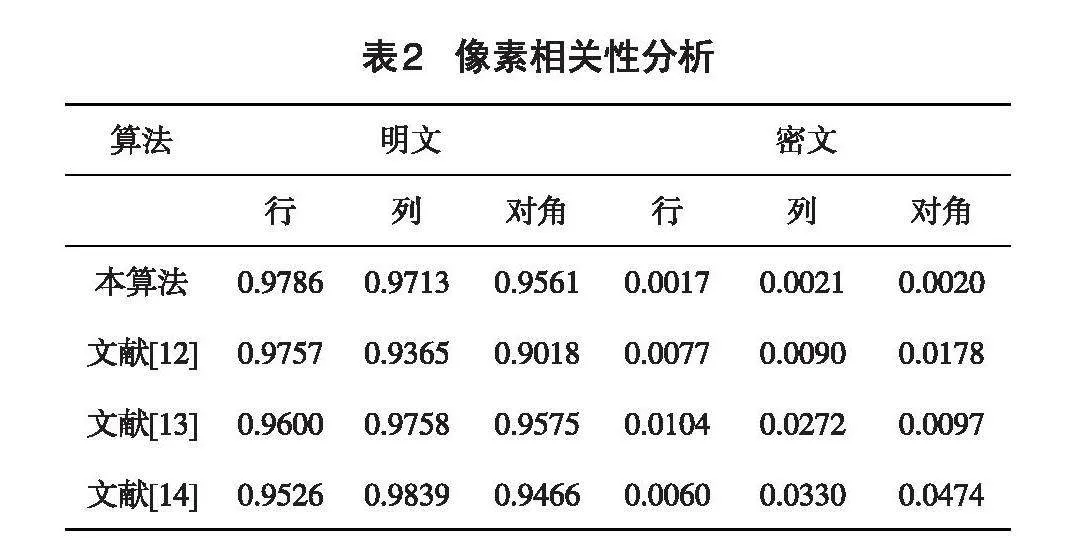
為充分驗證該算法有效性，表2列出了基于多吸引子混沌系統加密算法與其他算法的對比數據，其相關性系數值說明本算法可以有效降低像素離散程度，安全性較好。

5 結論

本文基于Lorenz混沌系統設計了一種新型的多吸引子憶阻混沌系統應用到圖像加密中，以增強圖像加密的安全性能。首先，通過分岔圖、LE圖、相圖及復雜度圖分析了該系統動力學特性，驗證了系統具有超混沌特點及動態復雜性。基于此發現，提出高復雜度區間的混沌序列對圖像矩陣進行擴散、置亂和旋轉處理相結合的方案，通過直方圖、信息熵和相鄰像素相關性的分析等方法證明本加密方案可以很好地隱藏明文圖像的信息，加密效果較好。

［參考文獻］

［1］ 曹可，賴強，賴 聰.含多吸引子的憶阻混沌系統的分析與實現［J］.深圳大學學報，2022，39（4）：480-488.

［2］ 秦銘宏，賴 強，吳永紅.具有無窮共存吸引子的簡單憶阻混沌系統的分析與實現［J］.物理學報，2022，71（16）：146-156.

［3］ 顏閩秀，張 萍.保守系統的類混沌吸引子共存分析及圖像加密［J］.蘭州理工大學學報，2023，49（5）：102-111.

［4］ 高若云，白牡丹，黃佳鑫，等.基于多混沌系統的多圖像加密算法［J］.計算機系統應用，2024，33（3）：170-177.

［5］ 劉思洋，王越，李寒.基于超混沌系統及有限域的圖像加密算法［J］.河北師范大學學報，2024，48（2）：129-140.

［6］ 代文鵬，陳 恒，焦方桐，等.一類新型糾纏混沌系統的電路設計及在圖像加密中的應用［J］.廊坊師范學院學報（自然科學版），2023，23（1）：22-28.

［7］ 蔡正保.一種基于混沌加密和小波變換的數字水印技術研究［J］.廊坊師范學院學報（自然科學版），2016，16（2）：17-21.

［8］ 胡超飛，尹毅峰，劉琨鵬.基于序列密碼的圖像加密算法［J］.湖北民族大學學報，2021，39（1）：67-71.

［9］ 杜傳紅，劉立才，張謝馥，等.模擬Lorenz混沌系統電路設計［J］.科技創新與應用，2017（10）：24.

［10］ 韋斌，隋宇，鄧小玉，等.基于頻域壓縮和二維離散混沌的圖像加密方案［J］.計算技術與自動化，2023，42（4）：110-116.

［11］ 郭現峰，李浩華，魏金玉.基于Fibonacci變換和改進Logistic-Tent混沌映射的圖像加密方案［J］.吉林大學學報，2023，53（7）：2115-2120.

［12］ 王偉杰，姜美美，王淑梅，等.基于量子長短期記憶網絡的量子圖像混沌加密方案［J］.物理學報，2023，72（12）：21-32.

［13］ 張勛才，劉奕杉，崔光照.基于 DNA 編碼和超混沌系統的圖像加密算法［J］.計算機應用研究，2019，36（4）：1139-1143.

［14］ LI W， CHANG X Y， YAN A M， et al. Asymmetric Multi- ple Image Elliptic Curve Cryptography［J］.Optics and Lasers in Engineering， 2021， 136： 1-10.

［15］ FIRDOUS A，UR REHMAN A，SAAD MISSEN M M. A Highly Efficient Color Image Encryption Based on Linear Transformation Using Chaos Theory and SHA-2 ［J］.Multimedia Tools and Applications， 2019， 78（17）： 24809-24835.

責任編輯 呂榮榮

［收稿日期］ 2024-05-11

［基金項目］ 陜西省重點研發計劃（2018GY-091）；西安市科技創新引導項目（201805043YD21CG27-2）

［作者簡介］ 代文鵬（1991- ），男，碩士，煙臺科技學院海洋工程學院教師，研究方向：開關電源與混沌控制。

［通訊作者］ 陳恒（1965- ），男，博士，西京學院副教授，研究方向：混沌控制與機器人技術。