分類討論思想在解決幾何問題中的應用

摘 要：幾何探索性問題是歷年中考的熱點，經常以中考壓軸題的形式出現.這類問題綜合性強，涉及的知識點多，解法靈活多樣，承載著一定的選拔功能，對學生而言具有一定的難度.在解決這類問題的過程中，通常需綜合運用多種數學思想與方法.基于此，以一道中考試題為例，重點分析分類討論思想在解決幾何壓軸題中的應用，以期為初中數學教學提供參考.

關鍵詞：分類討論思想；幾何問題；壓軸題；應用

中圖分類號：G632 文獻標識碼：A 文章編號：1008-0333（2024）29-0008-03

收稿日期：2024-07-15

作者簡介：仇春學（1979.1—），男，陜西省大荔縣人，本科，中學一級教師，從事初中數學教學研究.

中考壓軸題一般為幾何探索題，具有開放性和綜合性的特點，考查的知識點較為全面，涉及多種數學思想與方法，對學生而言具有一定的難度. 筆者以2023年深圳市中考數學第22題為例，探討分類討論思想在解決幾何問題中的應用，供讀者參考.

1 試題呈現

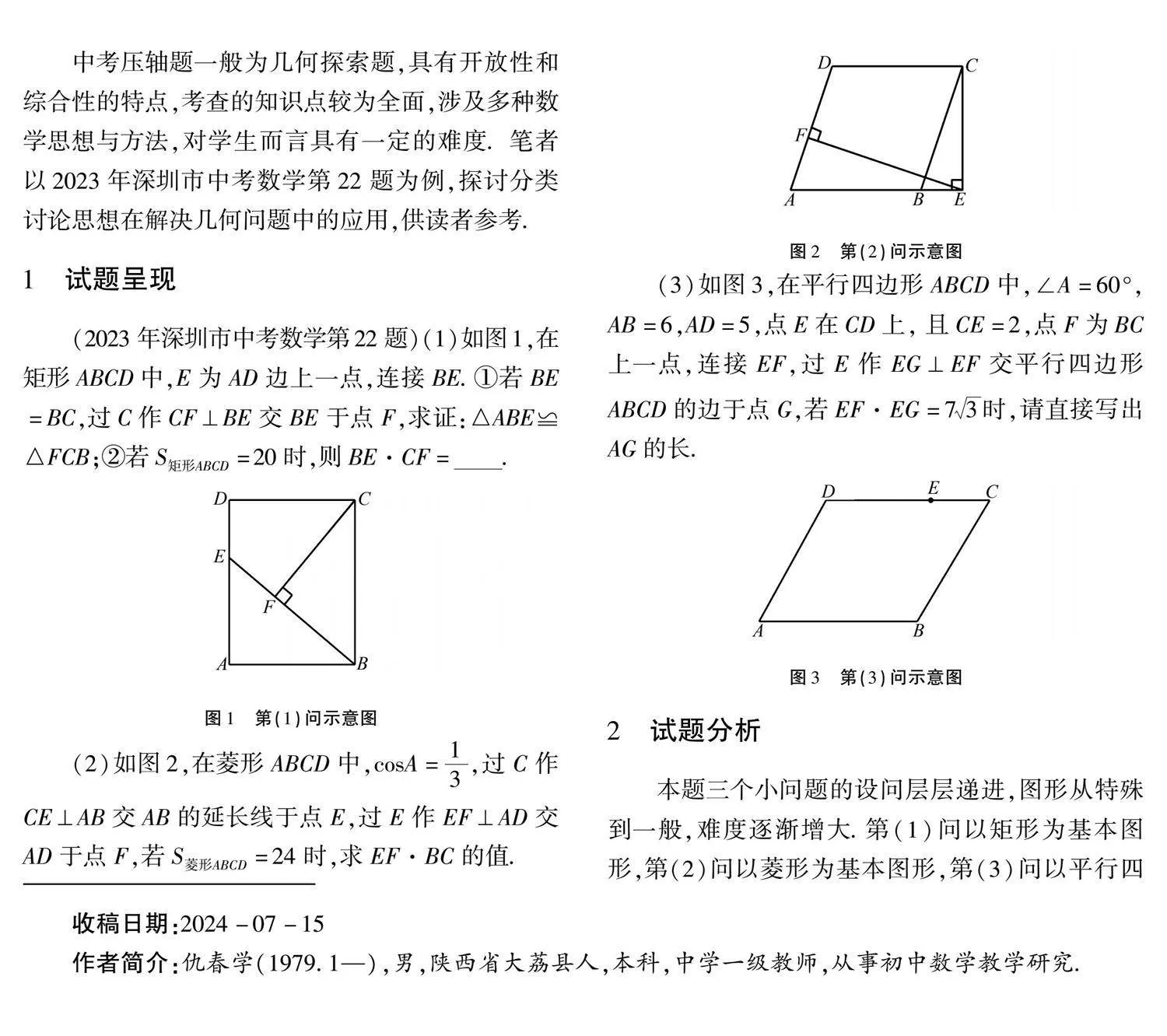
（2023年深圳市中考數學第22題）（1）如圖1，在矩形ABCD中，E為AD邊上一點，連接BE.①若BE=BC，過C作CF⊥BE交BE于點F，求證：△ABE≌△FCB；②若S 矩形ABCD=20時，則BE·CF=_______．

（2）如圖2，在菱形ABCD中，cosA=13，過C作CE⊥AB交AB的延長線于點E，過E作EF⊥AD交AD于點F，若S 菱形ABCD=24時，求EF·BC的值.

（3）如圖3，在平行四邊形ABCD中，∠A=60°，AB=6，AD=5，點E在CD上， 且CE=2，點F為BC上一點，連接EF，過E作EG⊥EF交平行四邊形ABCD的邊于點G，若EF·EG=73時，請直接寫出AG的長.

2 試題分析

本題三個小問題的設問層層遞進，圖形從特殊到一般，難度逐漸增大.第（1）問以矩形為基本圖形，第（2）問以菱形為基本圖形，第（3）問以平行四邊形為基本圖形［1］.從知識點上看，本題主要考查矩形的性質、全等三角形的性質與判定、菱形的性質、解直角三角形、相似三角形的性質與判定、平行四邊形的性質等知識.從思想方法上看，本題考查分類討論思想、轉化與化歸思想、模型思想、方程思想等數學思想方法.因此，本題的綜合性較強，對學生分析問題和解決問題的能力有較高的要求，是一道具有一定區分度的中考壓軸題.

3 解法賞析

第（1）問較簡單，根據矩形的性質可得∠ABE+∠CBF=90°，又由CF⊥BE可知∠FCB+∠CBF=90°，從而可證明∠FCB=∠ABE.結合已知條件BE=BC，可證明△ABE≌△FCB，從而AB=CF，因此BE·CF=BC·AB=S 矩形ABCD=20.

評析 第（1）問主要考查矩形的性質、矩形的面積公式、全等三角形的判定與性質，屬于基礎題.

第（2）問也比較容易，根據菱形的性質可得AD//BC，所以∠CBE=∠EAF.又因為EF⊥AD，CE⊥AB，所以∠AFE=∠BEC=90°，所以△AFE∽△BEC，所以AEBC=EFCE=AFBE，所以EF·BC=AE·CE.又因為cosA=13且∠CBE=∠A，所以BE=BC·cos∠CBE=BC×cosA=13BC，所以AE=AB+BE=AB+13BC=AB+13AB=43AB，即EF·BC=AE·CE=43AB×CE=43S菱形ABCD=43×24=32.

評析 第（2）問主要考查菱形的性質、相似三角形的判定與性質、銳角三角函數的概念、線段關系的轉化等知識，屬于中低檔題.

第（3）問是本題的難點，下面進行詳細分析.

分析 此問的難點在于點G的位置不確定.一些學生缺乏分類討論思想，誤以為點G只能在AD邊上，從而造成漏解.事實上，點G可能在AD邊上、AB邊上或BC邊上，因此，要分三種情況討論，要求學生具備分類討論思想［2］.

①當點G在AD邊上時，如圖4，延長FE，交AD的延長線于點M，連接GF，過點E作EH⊥DM于點H.

因為四邊形ABCD是平行四邊形，AB=6，CE=2，所以CD=AB=6，DE=DC-EC=6-2=4.因為DM//FC，所以△EDM∽△ECF，所以EMEF=EDEC=2.考慮△MGE和△FEG，它們以GE為公共高，所以S△MGES△FEG=EMEF=2，所以S△MGE=2SΔEFG=EF·EG=73.在Rt△DEH中，∠HDE=∠A=60°，則EH=32DE=32×4=23，DH=12DE=2，所以12MG×HE=3MG=73，所以MG=7.又GE⊥EF，EH⊥MG，所以∠MEH=90°-∠HEG=∠HGE，所以△MEH∽△EGH，所以HEHG=HMHE，即HE2=HM·HG.設AG=a，則GD=AD-AG=5-a，GH=GD+HD=5-a+2=7-a，HM=GM-GH=7-（7-a）=a，所以（23）2=a（7-a），解得a=3或a=4，從而可知AG=3或AG=4.

評析 對于點G在AD邊上的情況，其解題過程分為以下幾步：一是先將FE延長與AD的延長線相交于點M，由“X型”相似模型可證△EDM∽△ECF，從而由相似三角形的性質可得EM=2EF；二是根據已知條件EF·EG=73可得到2S△EFG=73，再根據△MGE和△FEG共高可得S△MGE=2S△EFG=73；三是考慮△MGE的底邊MG，這條邊上的高可以根據含30°角的直角三角形的性質求出，從而利用等面積法即可求出MG；四是根據關系HE2=HM·HG求出AG.事實上，關系式HE2=HM·HG即為射影定理，但由于射影定理不是初中數學教材中的結論，所以在以上解答中，給出了關系式HE2=HM·HG的證明過程.

②當點G在AB邊上時，如圖5，連接GF，延長GE交BC的延長線于點M，過點G作GN∥AD，則GN∥BC，四邊形ADNG是平行四邊形.

設AG=x，易知DN=AG=x，EN=DE-DN=4-x.因為GN∥CM，所以△ENG∽△ECM，所以EGEM=GNCM=ENEC=4-x2，所以CM=2GN4-x=104-x.考慮△GEF和△MEF，它們以EF為公共高，所以SΔGEFS△MEF=EGEM=ENEC=4-x2，又因為2S△GEF=EF·EG=73，所以S△MEF=2S△GEF4-x=734-x.過點E作EH⊥BC于點H，在Rt△EHC中，EC=2，∠ECH=60°，所以EH=3，CH=1，所以S△MEF=12×MF×EH，則12×3×MF=734-x，所以MF=144-x，所以MH=CM+CH=104-x+1=14-x4-x，FH=MF-MH=144-x-14-x4-x=x4-x.因為∠MEF=∠EHM=90°，所以∠FEH=90°-∠MEH=∠EMH，所以△FEH∽△EMH，所以FHEH=EHMH，所以EH2=FH·MH，即（3）2=x4-x×14-x4-x，解得x1=32，x2=8（舍去），即AG=32.

評析 對于點G在AB邊上的情況，其解題過程與情形①類似，分為以下幾步：一是設AG=x，將GE延長與BC的延長線相交于點M，構造“X型”相似模型，證明△ENG∽△ECM，再由相似三角形邊的比例關系求出CM的表達式；二是根據△GEF和△MEF共高和條件EF·EG=73可得S△MEF的表達式；三是利用等面積法可得MF的表達式；四是根據關系EH2=FH·MH列出方程，從而求出AG.

③當G點在BC邊上時，如圖6，過點B作BT⊥DC于點T，則S△BTC＞S△EFG.

在Rt△BTC中，CT=12BC=52，BT=3TC=532，S△BTC=12BT×TC=12×532×52=2538.因為EF·EG=73，所以S△EFG=723.因為2583＜723，即S△BTC＜S△EFG，矛盾.故G點不可能在BC邊上.

綜上所述，AG的長為 3或4或32.

4 結束語

在初中階段，分類討論思想已經得到了廣泛應用，但學生的分類討論思想較為薄弱，因此，在中考試題中合理滲透分類討論思想有利于選拔具備較高數學素養的學生.在平時教學中，教師要向學生滲透分類討論思想，引導學生利用分類討論思想解決問題，提高學生運用所學知識分析問題和解決問題的能力，提升學生的數學核心素養.

參考文獻：［1］ 徐茜敏.分類討論：建構初中數學嚴謹的思維方式［J］.數理天地（初中版），2023（11）：56-58.

［2］ 沈俊杰.分類討論思想在初中數學解題中的應用［J］. 中學數學（下半月），2023（8）：52-53.

［責任編輯：李 璟］