以“問”促“學”

摘 要：隨著課程改革的不斷推進，傳統的教育模式和教學理念已經難以滿足現代教育需求，教育教學的改革勢在必行.在初中數學教學中，以問題為導向，促使學生進行深層次思考，有利于學生主動探究數學知識，培養學生的邏輯思維能力，提升學生的學習效果，幫助學生建立完整的知識體系，全面提升學生的數學素養.基于此，文章圍繞以“問”促“學”教學方法，對初中數學問題導向策略進行探究，以期為初中數學教學提供參考.

關鍵詞：初中數學；數學教學；問題導向策略；應用

中圖分類號：G632 文獻標識碼：A 文章編號：1008-0333（2024）29-0035-03

收稿日期：2024-07-15

作者簡介：盧玉琴（1979.10—），女，江蘇省蘇州人，本科，中小學一級教師，從事初中數學教學研究.

美國著名數學家哈爾莫斯曾說過，問題是數學的心臟.他強調圍繞問題展開數學教學，即數學教學需要以問題為中心，以問題驅動教學，讓學生在解決問題的過程中理解相應的概念與定理.基于此，在初中數學教學中，教師可通過設計不同的問題引導學生學習，并以問題促進學生學習，提升學生的學習效率，發展學生的核心素養.

1 設計生活化問題，培養模型構建意識

數學是一門與生活實際息息相關的學科，源于生活，根植于生活.數學是解決生活問題的鑰匙，也是人們生活、學習必不可少的工具.在初中數學教學中，教師可以將各種生活化的內容引入課堂，引發學生的“生活思考”.由此拉近學生與數學的距離，并讓學生在比較熟悉的問題情境中主動探索數學知識，同時激發學生的學習興趣，使數學教學達到事半功倍的效果.

例如，在學習“等腰三角形”時，為了讓學生更好地理解軸對稱圖形的內涵及等腰三角形的有關性質，教師可引入生活中的“蓋房子”問題，以此激發學生的探索熱情，有助于學生深入學習新知識.

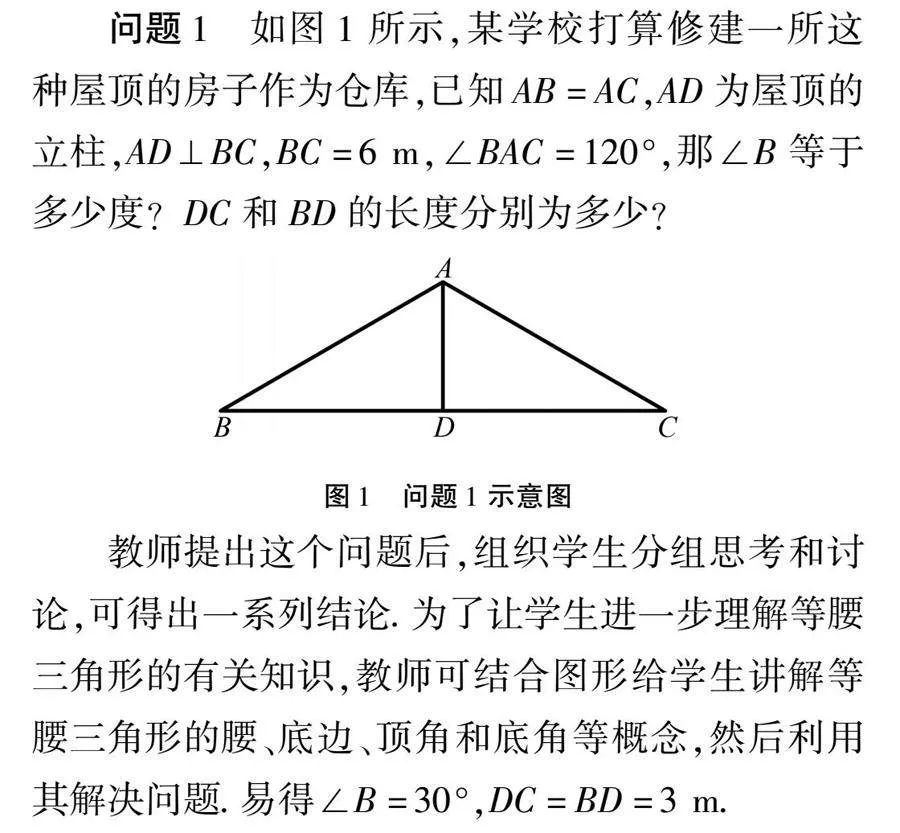
問題1 如圖1所示，某學校打算修建一所這種屋頂的房子作為倉庫，已知AB=AC，AD為屋頂的立柱，AD⊥BC，BC=6 m，∠BAC=120°，那∠B等于多少度？DC和BD的長度分別為多少？

教師提出這個問題后，組織學生分組思考和討論，可得出一系列結論.為了讓學生進一步理解等腰三角形的有關知識，教師可結合圖形給學生講解等腰三角形的腰、底邊、頂角和底角等概念，然后利用其解決問題.易得∠B=30°，DC=BD=3 m.

在教學過程中，教師提出生活化的數學問題，能夠激發學生思考的積極性，繼而完成對知識的深層次思考和學習.在問題1中，學生對等腰三角形的學習經歷了由具體的“物”到抽象的“形”的過程，建立起了等腰三角形的直觀模型，不但提升了教學效果，而且對培養學生的學習興趣有重要作用.

2 設計并列式問題，深化分類討論思想

新課程標準強調，在初中數學教學中，教師應引導學生主動思考，并教會學生如何思考，提升學生的數學思維能力.筆者認為，以“問”促“學”的教學方法能使學生置身于問題情境中，在教師的引導下自主篩選信息、分析和解決問題，從而達到訓練學生思維和問題解決能力的目的.這種方法將學生置于問題解決者的地位，培養學生思考解決問題的能力，促進學生掌握基礎知識與基本技能.在初中數學教學實踐中，教師要善于激發學生對知識的興趣，調動學生的非智力因素，引發學生對知識的深度思考，完成高質量的探究學習.

例如，在學習“圓”時，對于“點與圓的位置關系”“一弦對兩弧”“圓心與弦的位置關系”等問題，學生很容易出現錯誤.為此，在教學過程中，教師可為學生設計相應的“學習陷阱”，以此引發學生更深層次的思考，提高學生對已知條件的辨別和處理能力，從而提高學生分析問題和解決問題的能力.

比如，對于“點與圓的位置關系”，學生經常會忽視一種情況，因此教師設計如下相應的“陷阱”.

陷阱1：點Q是⊙O所在平面內的一個定點，若點Q到圓上一點的最大距離和最小距離分別是16和6，則該圓的直徑為多少？

陷阱2：點Q是⊙O所在平面內的一個定點，⊙O半徑2，若點Q到圓上點的最小距離1，則點Q到⊙O上點的最大距離是多少？

教師提出問題后，雖然有的學生快速地說出了答案，但卻掉進了教師設計的“陷阱”中，忽視了其中的一種情況.在教學過程中，教師不必急于否定學生的答案，而是讓學生繼續思考，激發學生的挑戰意識，將學生的思維引向更深的層次.學生仔細思考以后，最終會發現問題的陷阱所在.

3 設計遞進式問題，提升邏輯思維能力

數學知識之間普遍存在著緊密聯系.在教學實踐中，教師要善于對學生進行引導，幫助學生構建更為完善的知識體系，進而促使學生思維能力、推理能力不斷發展.因此，教師可以根據教學內容，設計“問題鏈條”，以促使學生深度思考，提升學生學習效率，從而實現能力與素養的培養［1］.

例如，在學習“一次函數”時，教師可設計一個“問題鏈條”，以此還帶領學生開展探究性學習.

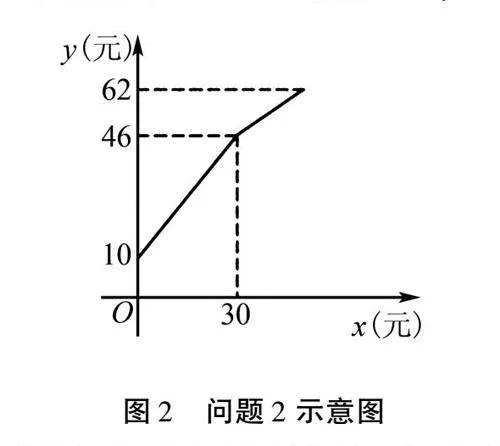
問題2 水果店老板賣西瓜，提前準備了一些零錢備用，他先按照市場價格賣了一些西瓜，然后又降價賣了一些，他手中的錢的數量和西瓜重量的關系如圖2所示，請思考如下問題：

（1）水果店老板一共準備了多少零錢？

（2）降價之前，每千克西瓜的售價是多少元？

（3）如果降價之后按照每千克0.8元的價格將西瓜賣完，這時水果店老板手中的錢數一共是62元，請問他一共購進了多少千克西瓜？

設計從易到難、層層遞進的“問題鏈條”，能夠幫助學生對問題展開探究性思考，使學生快速掌握問題的核心，為其在短時間內解決問題創造便利條件.遞進式問題不但能夠調動學生的學習熱情，而且能夠有效提升課堂教學效率.

4 設計引導式問題，突破難點內容學習

在初中數學教學中，不僅要重視基礎知識教學，而且要重視培養數學思想，讓學生在思考和學習的過程中逐步把握數學知識的內涵，抓住數學的“靈魂”，進而完成高質量的探究學習.為此，教師可以設計引導式問題.問題的設計應重視內容的選取，遵循學生的認知發展規律.在問題解決過程中，教師應引導學生理解和掌握思考方法，促使學生的數學素養不斷發展.

例如，在學習“相似三角形”時，教師可圍繞“相似三角形的性質和判定”優化教學，設計相應的問題讓學生思考，由此突破教學的重點和難點，并幫助學生掌握思考的方法.

問題3 如圖3，點D是△ABC的邊BC上的一個點，已知BD∶DC=2∶1，E是AD的中點，連接BE并延長交AC于F，那BE∶EF的值是多少？

為此，教師可提出兩個相關的思考性問題：

（1）欲求兩條線段的比值，一般需證明三角形相似.在此題中，哪對三角形是你要選擇的證明對象？

（2）圖3中有沒有與△AEF相似的三角形？如果沒有與其相似的三角形，該如何解決本題？

此問題能夠為學生提供思考方法.學生按照這種方法思考，能夠成功鎖定△AEF為證明的目標之一.隨后繼續進行深層次思考，不能找出與△AEF相似的三角形，從而可選擇其他方式構造三角形，使其與△AEF相似，繼而完成問題的解答.

在整個思考和解決問題的過程中，教師通過引導式問題，為學生提供思考的方法，并且在逐步深入探索的過程中，能夠完成對有關重點和難點知識的理解，使學生掌握數學學習的方法.

5 設計差異化問題，助力課后內化遷移

數學教學模式的優化涵蓋各個教學環節，其中包含課后鞏固思考.課后練習有助于學生鞏固所學知識，并讓學生在遷移運用中內化所學知識，提升數學能力［2］.因此，教師可在課后通過“問題引入”促進學生的深度學習，幫助學生“當堂學習，當堂消化”，

掌握基礎知識，實現高質量學習.

例如，在學習“一元二次方程”后，教師可根據班級學生的實際情況，將其劃分成“A”“B”“C”三個層次，并設計相應的問題.問題的設置需兼顧普適性與深入性原則，既要保證全體學生積極參與，又要具有一定的討論、探究價值.

“A”層次針對基礎薄弱的學生，主要問題有：

（1）方程x2-75x+350=0，3x2-6x=20是一元二次方程嗎？

（2）自編兩個一元二次方程.

對于這個層次的學生，需強化其數學學習自信心和學習興趣，設計這樣的問題能夠達到此目的.

“B”層次針對中等水平學生，提出的問題有：

（1）方程x2-x=44，1x2-9x-90=0是不是一元二次方程？它們有什么共同點和不同點？

（2）在x-2x2+5=0，4x2-5y-1=0，ax2+bx+c=0，（m-1）2=1中，哪些是一元二次方程？

對于這個層次的學生，需要培養其克服困難的信心和決心，這樣的問題設計可以強化學生對基本概念的理解，并獲得成就感，使其在今后學習遇到困難時能自己解決問題.

“C”層次針對能力較好的學生，

可設計這樣一道問題：

如果方程（m+1）x|4m|-2+27mx+5=0是關于x一元二次方程，那么m的值為多少？

對于這個層次的學生，需激勵他們突破自我，向更好的方向發展.設計這樣的問題，能夠使學生綜合已學知識，構建更為完善的知識體系.

6 結束語

在初中數學教學中，合理運用問題導向策略，可以更好地激發學生探究學習的熱情，讓學生在思考的過程中深化對知識的理解，不斷提升數學核心素養.為此，教師可以圍繞“以問促學”的理念優化教學模式，引導學生學習與探索，鍛煉其思維能力，讓學生從“問題”中獲得知識與能力，進而完成對學生核心素養的培養.

參考文獻：［1］ 何強.問題導學法在小學數學教學中的運用實踐［J］.基礎教育論壇，2022（35）：87-88.

［2］ 任亞男.問題導學法在初中數學課堂中的運用策略［J］.當代家庭教育， 2022（29）：125-128.

［責任編輯：李 璟］