基于深度學習的鐵路信號傳輸節點異常干擾預測

摘要：針對鐵路信號傳輸過程中頻率波動導致的預測誤差問題，文章設計了一種基于深度學習的異常干擾預測方法。該方法全面獲取節點干擾數據，利用數據處理技術提取關鍵特征，反映信號異常情況。基于深度學習算法，文章構建了干擾信號異常檢測框架，自動學習和識別異常模式。通過實時數據輸入，該框架能迅速輸出預測結果，準確預測異常干擾。實驗證明，該方法平均預測誤差距離為50.5 kHz，相比對照組降低85 kHz以上，實現了對鐵路信號傳輸節點異常干擾的精準預測，為鐵路安全穩定運行提供了有力保障。

關鍵詞：深度學習模型；鐵路信號；傳輸節點；異常干擾預測；時域偏度

中圖分類號：TP399 文獻標志碼：A

0 引言

隨著鐵路交通的快速發展，鐵路信號系統作為保障列車安全、高效運行的關鍵環節，其穩定性和可靠性顯得尤為重要。在實際鐵路信號傳輸節點異常干擾預測中，賈志超［1］研究了無線電通信過程中干擾信號的來源、特性及傳播規律。該方法通過增益分析，精確識別并定位干擾信號，有效提高了干擾信號查找的準確性和效率。蘆偉東［2］通過對實際鐵路信號數據的分析，構建了合適的ARIMA模型并成功應用于異常干擾信號的預測。然而，該模型在實際運行過程中仍存在一些問題，導致信號傳輸質量下降甚至中斷，給鐵路運營帶來安全隱患。因此，本文提出基于深度學習的鐵路信號傳輸節點異常干擾預測方法。

1 獲取鐵路信號傳輸節點干擾數據

本文采用頻譜分析儀［3］對鐵路信號傳輸節點的干擾數據進行精確采集，實時捕捉并分析信號發送設備發出的高頻無線電信號X（t）在傳輸過程中受到的各類干擾。獲取的鐵路信號傳輸節點干擾數據為：

Y（t）=X（t）+N（t）+Z（t）（1）

式中：N（t）表示在信號傳輸過程中引入的干擾信號，Z（t）表示傳輸過程中的噪聲信號，t表示信號傳輸時間。

針對原始數據中摻雜的噪聲信號，本文采用小波閾值去噪法濾除噪聲，得到去噪后的信號如式（2）所示。

Y′（t）=IDWTW，W≥λ

0，W<λ（2）

式中：IDWT表示小波逆變換，W表示含噪信號的小波系數，λ表示閾值。

將大于閾值的小波系數保留下來，再進行反變換，得到清晰的信號。

2 提取鐵路信號傳輸節點干擾數據異常特征

構建鐵路信號傳輸節點干擾數據的觀測矩陣，考慮到傅里葉基函數的特性，本文選取了能夠反映數據高頻分量和長期平穩分量的參數作為基準［5］，從而形成了特定的基準函數。小波逆變換得到的去噪處理的鐵路信號傳輸節點干擾數據，這r7dzUTTtp9apq6++kYeMT0Q4IlQJFvYA4icMpQLCDcQ=些數據與基準函數共同構成了觀察矩陣的構建基礎。為了確保特征提取結果的準確性，本文分別針對不同特征展開提取，主要包含以下幾種：

2.1 時域內的偏度

在時域分析中，偏度是一個重要的統計量，用于衡量數據分布的偏斜程度。針對鐵路信號傳輸節點干擾數據，提取其在不同時域波形下的偏度特征。計算公式為：

S=n∑ni=1（xi-x）3（n-1）（n-2）σ3（3）

式中：n表示數據點的數量，xi表示每個數據點，x表示數據的均值，σ表示數據的標準差。偏度值大于觀察矩陣表示鐵路信號傳輸節點干擾數據異常右偏，小于觀察矩陣表示鐵路信號傳輸節點干擾數據異常左偏，接近觀察矩陣則表示鐵路信號傳輸節點干擾數據分布相對對稱。

2.2 包絡起伏程度

在深入研究鐵路信號傳輸節點干擾數據時，包絡起伏程度的計算是揭示數據動態特性的關鍵。包絡起伏主要由信號波峰的變動情況決定，因此，可以通過計算波峰間的差異和變化趨勢來量化這一異常特性。具體的計算式可以基于信號波峰的高度差進行設計。k是波峰的索引，相鄰波峰間的高度差h（k）：

h（k）=x（k）-x（k-1）（4）

2.3 瞬態能量

在提取鐵路信號傳輸節點干擾數據的瞬態能量異常特征時，瞬態能量通常與信號的幅度和頻率的快速變化相關。因此，通過計算信號的短時能量來量化這一特征。

每幀的瞬態能量E可以通過計算該幀內信號幅度的平方和來得到，公式如下：

E=∑Nn=1|xi（n）|2（5）

式中：N表示每幀信號的長度，xi（n）表示第i幀信號。通過比較不同幀的能量值，可以識別出能量異常的區域，這些區域可能對應于信號中的瞬態干擾。

3 利用深度學習構建干擾信號異常檢測框

深度學習模型不僅擁有強大的泛化能力，能應對多樣化的干擾信號異常檢測場景，還能通過大量數據的訓練，持續優化自身性能，從而確保檢測結果的準確性和可靠性。本文利用訓練好的深度學習模型對新的鐵路信號傳輸節點干擾數據進行異常檢測。通過計算輸入數據的特征表示與模型學習到的正常信號特征之間的距離或相似度，可以判斷該數據是否存在異常。如果存在異常，則進一步利用模型輸出的異常類別或概率信息進行標識和處理。

默認初始深度學習模型為干擾信號異常檢測框，在設置2∶1縱橫比的錨框后，深度學習模型能夠更精確地處理干擾信號異常檢測的像素點。假設錨框的寬度為w，高度為h，對于每個像素點（x，y），以其為中心，根據錨框的尺寸w和h來定義一個候選區域。這個候選區域的左上角坐標為x-w2，y-h2，右下角坐標為x+w2，y+h2。候選區域的數學公式可表示為：

L=（R，Q）x-w2<R<x+w2

y-h2<Q<y+h2（6）

式中：R表示候選區域橫坐標邊界，Q表示候選區域縱坐標邊界。

將候選區域的橫縱坐標邊界作為檢測框的觸發閾值，能夠精確地控制檢測框的檢測范圍，確保干擾信號異常特征被有效捕捉。在限定的檢測框面積內，本文制定了一套鐵路信號傳輸節點干擾數據異常識別流程，通過對候選區域內信號特征的分析和比對，準確判斷是否存在異常。如果存在異常干擾，將及時發出警報并采取相應的措施進行處理。

4 實驗

4.1 實驗準備

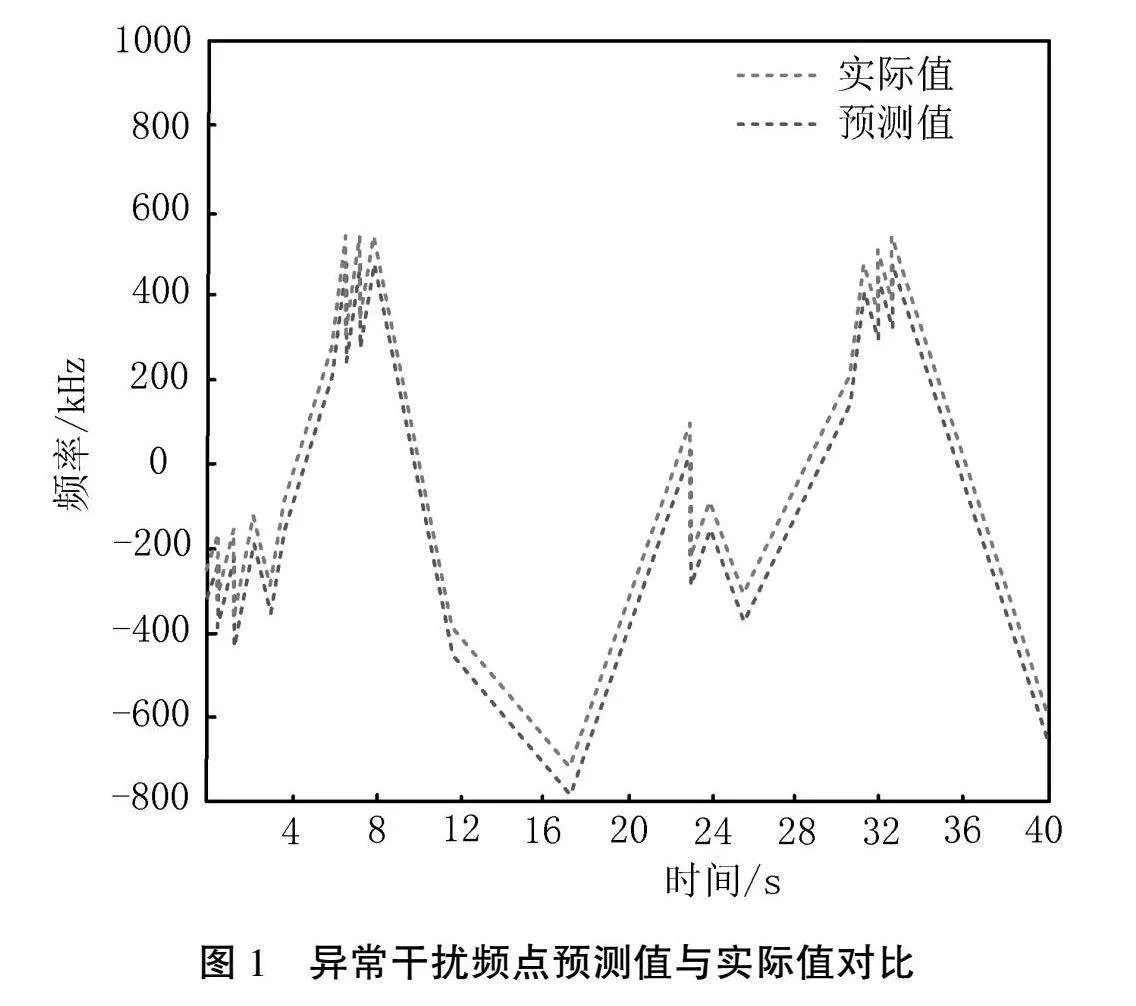
本文選用某鐵路信號的實測數據作為實驗樣本。異常干擾信號仿真參數設置：采樣頻率1000 Hz，干擾功率-50～-10 dBm，干擾寬帶1～10 MHz，初始距離1～10 km，感知時間20 s。捕捉到10個具有顯著影響的異常干擾頻點，得到30000點有效數據。隨機抽取了樣本數據中的40點進行預測并將預測結果與實際干擾頻點進行了對比，如圖1所示。

由圖2可知，本文方法異常干擾頻點預測值與實際值基本一致，表明該方法的預測準確率達到了95%以上。

4.2 實驗結果分析

本文選用賈志超［1］提出的方法、蘆偉東［2］提出的方法為對比方法，分別為方法1和方法2。各方法下預測誤差距離如表1所示。

從表1中對比數據可以看出，方法1和方法2在預測鐵路信號異常干擾時，預測頻率與實際頻率差值較大，常超120 kHz，平均誤差分別為139.3 kHz和135.7 kHz。而本文方法預測誤差顯著減小，平均僅為50.5 kHz，相比對照組分別降低88.8 kHz和85.2 kHz。這一顯著改進證明本文方法能更精準地預測鐵路信號傳輸節點異常干擾，為鐵路安全提供有力保障。

5 結語

基于深度學習的鐵路信號傳輸節點異常干擾預測研究，不僅提升了預測精度，更為鐵路信號傳輸的安全穩定提供了堅實的技術支撐。通過深度挖掘數據特征，本文方法有效捕捉了異常干擾信號的細微變化，實現了精準預測。

參考文獻

［1］賈志超.基于增益分析的無線電通信干擾信號查找及預測方法［J］.長江信息通信，2023（8）：163-166.

［2］蘆偉東.基于ARIMA的干擾信號發射規律預測［J］.中國無線電，2022（6）：65-67.

［3］趙宏澤，魏光輝，杜雪，等.雷達裝備二階互調偽信號干擾效應預測模型［J］.強激光與粒子束，2023（8）：93-101.

［4］鮮娟，張宗琪，諶麗，等.電子通信網絡雙頻突變信號抗干擾預測方法［J］.計算機仿真，2022（8）：403-406，518.

［5］張慶龍，王玉明，程二威，等.導航接收機跟蹤環路電磁干擾的預測方法研究［J］.電子與信息學報，2021（12）：3656-3661.

（編輯 王雪芬）

Abnormal interference prediction of railway signal transmission nodes based on deep learning

ZHU Dehua

（Shuohuang Railway Development Co.， Ltd.， Yuanping 034100， China）

Abstract： In response to the prediction error caused by frequency fluctuations in railway signal transmission， this article proposes a deep learning based anomaly interference prediction method. This method comprehensively obtains node interference data， extracts key features using data processing techniques， and reflects signal anomalies. Based on deep learning algorithms， construct an interference signal anomaly detection framework to automatically learn and recognize abnormal patterns. Through real-time data input， the framework can quickly output prediction results and accurately predict abnormal interference. Experimental results have shown that the average prediction error distance of this method is 50.5 kHz， which is more than 85 kHz lower than the control group. It achieves accurate prediction of abnormal interference in railway signal transmission nodes and provides strong guarantees for the safe and stable operation of railways.

Key words： deep learning model; railway signal; transmission node; abnormal interference prediction; time domain skewness