深度學習

【摘要】本文通過具體的實例，分析動能定理在解決多過程問題、流體模型中的功率問題、小車以恒定功率運動時的位移問題等不同類型力學問題中的有效性和優越性，強調其在簡化問題求解過程、提高解題效率方面的重要作用，期望對學生的學習有所幫助．

【關鍵詞】動能定理；力學問題；應用實例

力學是物理學的重要分支，解決力學問題是物理學學習和研究的重要內容．在眾多的力學定理中，動能定理以其獨特的優勢在求解力學問題時發揮著重要作用．動能定理不僅能夠簡化問題的分析過程，還能夠幫助學生更深入地理解物體的運動規律．

1 求解多過程問題

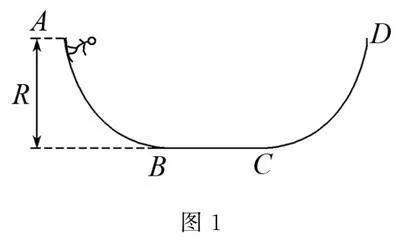
例1 圖1為某單板滑雪U型池的比賽場地的橫截面圖，其中AB段和CD段為半徑R=4m的14光滑圓弧雪道，BC段是長為4.5m的水平雪道，兩銜接點處與圓弧雪道平滑連接．有一質量為m=60kg（含滑板）且可視為質點的運動員以5 m/s的速度從A點沿切線滑下后，始終保持在一個豎直平面內運動，經U型雪道從D點豎直向上飛出，經t＝0.8s恰好落回D點，然后又從D點返回U型雪道．不計空氣阻力，重力加速度g取10 m/s2．求：

（1）運動員與BC雪道間的動摩擦因數；

（2）運動員第一次運動到C點時對雪道的壓力大小；

（3）運動員最后靜止處距離B點的距離.

解析 （1）根據題意，當運動員從D點沖出去后做豎直上拋運動，則vD=g·t2，

解得vD=4m/s，

運動員從A運動到D，根據動能定理，

有－μmglBC=12mv2D－12mv2A，

解得μ＝0.1．

（2）運動員從C運動到D，根據動能定理可得－mgR=12mv2D－12mv2C，

在C點，根據牛頓第二定律，有FN－mg=mv2CR，

聯立解得FN=2040N，

根據牛頓第三定律可得，運動員運動到圓弧最低點C點時對雪道的壓力大小為F′N=FN=2040N．

（3）運動員從A點開始運動到最終靜止，根據動能定理有mgR－μmgs=0－12mv2A

解得s=52.5m=11lBC+3m，

所以運動員最后靜止處距離B點的距離為l=lBC－3m=1.5m．

點評 運動員在軌道內做了若干次往返運動，運動過程比較復雜，但在AB段和CD段運動的過程中無機械能損失，只有BC段有機械能的損失，而動能定理解決這類多過程問題時，無需考慮中間的復雜過程，機械能的損失只與BC段走過的路程有關，根據動能定理列式求解即可．

2 求解流體模型中的功率問題

例2 脈沖水槍是夏季流行的一種水槍玩具，如圖2所示的脈沖水槍扣動一次扳機可以發射一顆出水時間很短的水流“子彈”．某同學在距地面高h處扣動一次扳機，“子彈”水平飛出，射程為x．已知水槍出水口面積為S，水的密度是ρ，重力加速度g，忽略一切阻力．求：

（1）水流“子彈”落地時間t；

（2）水流“子彈”發射速度大小v；

（3）扣動一次扳機水槍噴水的平均功率P．

解析 （1）水流“子彈”做平拋運動，在豎直方向做自由落體運動：h=12gt2，解得t=2hg．

（2）在水平方向做勻速直線運動：x=vt，解得v=xg2h．

（3）設扣動一次扳機水槍噴水時間為Δt，則噴水一次噴出水的質量為m=ρV=ρSvΔt，

水槍對噴出的水柱做的功全部轉化為水柱的動能，根據動能定理PΔt=12mv2，聯立，解得P=ρSx3g4hg2h．

點評 本題要求解扣動一次扳機水槍噴水的平均功率，表面上看起來無從下手，但如果借助流體模型的分析方法，設出水槍噴水時間為Δt，可進一步求出噴出水的質量，扣動一次扳機時水槍噴出的水獲得的動能等于水槍對水做的功，而做的功W=P·Δt，進而可以求出功率．

3 求解小車以恒定功率運動時的位移問題

例3 一玩具小車的質量為m=2kg，在水平地面上做勻速運動，電機的輸出功率為P=80W，某時刻無能量損失的運動到與水平夾角θ=53°的斜面上，在斜面上運動時電機的輸出功率不變，小車的速度大小與水平面上運動的速度大小相同，小車在水平面和斜面上運動時的阻力為小車對接觸面壓力的k倍，求：

（1）k的數值和小車的速度大小；

（2）某時刻電機的功率突然加倍，經時間2s小車在斜面上達到最終速度，求這段時間小車向上的位移．

解析 （1）在斜面上，根據平衡條件有F1=mgsinθ+kN，其中N=mgcosθ，P=F1v，

在水平面上，根據平衡條件有F2=kmg，其中P=F2v，

解得k=2，v=2m/s．

（2）小車最終達到穩定速度時有2P=F3v1，F3=mgsinθ+kN，

2s時間內，根據動能定理有2Pt－（mgsinθ+kN）x=12mv21－12mv2，解得x=7.7m．

點評 例3中，小車在斜面上運動時電機的輸出功率不變，可用W=2P·t求出牽引力的功率，再根據動能定理求解位移．

4 結語

動能定理作為力學中的重要定理，在解決各種力學問題中具有廣泛的應用．通過巧妙地運用動能定理，可以簡化問題的求解過程，提高解題的效率和準確性．在學習和應用中，學生應深刻理解動能定理的內涵，熟練掌握其應用方法，從而更好地解決力學問題，加深對物理世界的認識．

【項目基金：福建省教育科學“十四五”規劃2023年度專項課題《“四新”背景下大單元深度教學策略研究》（課題編號：閩教科規Fjxczx23-313）】

參考文獻：

[1]賈自泉，趙財昌.動能定理在動力學中的應用探討[J].數理化學習（高中版），2020（12）：48-49.

[2]徐梅.應用動能定理解決多過程運動問題[J].高中數理化，2023（20）：23-24.

[3]劉萬強，常濤.四種“變力作用下的運動”歸類例析——談如何優選動能定理或動量定理[J].高中數理化，2023（20）：27-29.