試論高中力學解題中整體法的應用

【摘要】物理作為極富邏輯性與抽象性的學科,需要學習的理論概念很多,對應的解題技巧掌握也是學生學好物理的關鍵.本文以案例分析的方式,討論高中物理力學解題中整體法的應用,以期分享經驗,引導學生更好的掌握力學解題技巧.
【關鍵詞】高中物理;力學;解題技巧
1 引言
力學解題是高中物理學習中的重要內容,但受力學知識抽象性和邏輯性較強的影響,解題難度較大,而在力學解題中引入整體法,則能夠將力學問題的解題思路與過程簡化,讓學生更好地將所學知識融會貫通,同時提升解題效率.
2 用整體法求解物體平衡問題
涉及物體平衡狀態下的受力情況的題目,在高中物理學習及高考中較為常見,而整體法也是解決此類題型較為常用的方法.
例1 如圖1所示,兩個質量都是m的小球A、B用輕桿連接后斜放在墻上處于平衡狀態.已知墻面光滑,水平地面粗糙.現將A球向下移動一小段距離.兩球再次達到平衡,那么將移動后的平衡狀態和原來的平衡狀態比較,地面對B球的支持力N和輕桿上的壓力F的變化情況是( )
(A)N不變,F變大. (B)N不變,F變小
(C)N變大,F變大(D)N變大,F變小
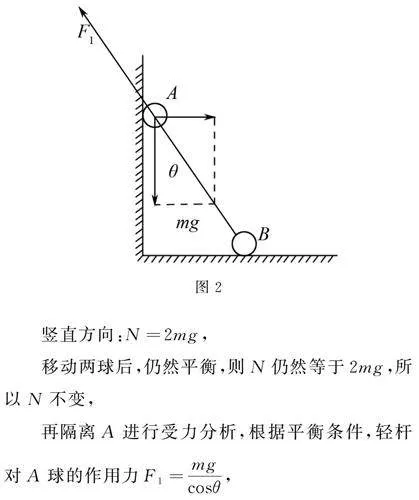
解 如圖2所示,對整體進行受力分析,
豎直方向:N=2mg,
移動兩球后,仍然平衡,則N仍然等于2mg,所以N不變,
再隔離A進行受力分析,根據平衡條件,輕桿對A球的作用力F1=mgcosθ,
根據牛頓第三定律可知,F=F1,
當A球向下移動一小段距離,夾角θ增大,cosθ變小,
所以F增大,故選項(A)正確,(B)(C)(D)錯誤.
小結 本題主要考查了力的合成與分解的運用和共點力的平衡問題.這一題目解題中,先運用了整體法,對整體受力情況進行分析,確定了地面對球B的支持力不變.又結合了隔離法,通過隔離分析,對桿子對球的作用力變化情況進行了分析.
3 用整體法求解連接體的問題
學生要解連接體問題需同時分析多個對象,各對象間的相互作用力關系也較為復雜.因此,解題難度較大.但是如果學生采用整體法就可以簡化解題過程,通過針對性分析完成解題.
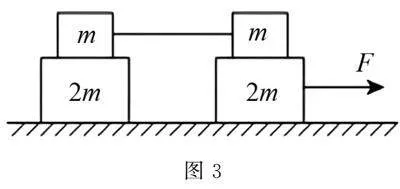
例2 如圖3所示,光滑水平面上放置著質量分別為m和2m的四個木塊,其中兩個質量為m的木塊間用一不可伸長的輕繩相連,木塊間的最大靜摩擦力是μmg.先用水平拉力F拉其中一個質量為2m的木塊,使四個木塊以同一加速度運動,求輕繩對m的最大拉力.
解 要想使四個木塊一起加速,則任意兩個木塊間的靜摩擦力都不能超過最大靜摩擦力.
設左側兩木塊間的摩擦力為F1,右側兩木塊間的摩擦力為F2,則對左側兩個木塊:
對2m有:F1=2ma①,
對m有:T-F1=ma②;
對右側兩個木塊:
對m有:F2-T=ma③,
對2m有:F-F2=2ma④;
聯立可得F=6ma,
四個物體加速度相同,由②+③得:
F2-F1=2ma⑤,
可知F2>F1,
故F2應達到最大靜摩擦力,由于兩個接觸面的最大靜摩擦力為μmg,
所以應有F2=μmg⑥,
聯立解得T=34μmg.
小結 首先要明確哪個物體最先達到最大靜摩擦力,再由整體法和隔離法求出拉力.要讓四個木塊一塊做加速運動而不產生相對運動,m與2m兩接觸面上的靜摩擦力不能超過最大靜摩擦力,而分析各木塊的受力可確定出哪一面上達到最大靜摩擦力,在此基礎上再結合牛頓第二定律即可求得最大拉力.
4 結語
總之,在高中物理力學題目的求解過程中引入整體法,可以讓學生在解題中簡化分析過程,準確把握解題關鍵技巧,進而引導學生學會從更宏觀的角度解決力學問題,這對于拓寬學生解題思路,強化學生力學知識掌握情況都有積極作用.
參考文獻:
[1]唐忠.高中物理力學解題中整體法運用分析[J].數理天地(高中版),2024(04):29-30.
[2]劉青.高中物理解題中整體法的應用研究[J].數理化解題研究,2023(36):92-94.
[3]呂娟.高中物理解題中整體法的應用[J].數理天地(高中版),2023(14):18-19.
[4]王輝.整體法和隔離法在高中物理解題中的應用思路[J].數理化解題研究,2023(19):126-128.

